mechanism design on:
[Wikipedia]
[Google]
[Amazon]
 Mechanism design (sometimes implementation theory or institution design) is a branch of
Mechanism design (sometimes implementation theory or institution design) is a branch of
 Mechanism design (sometimes implementation theory or institution design) is a branch of
Mechanism design (sometimes implementation theory or institution design) is a branch of economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
and game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
. It studies how to construct rules—called mechanisms or institutions—that produce good outcomes according to some predefined metric, even when the designer does not know the players' true preferences or what information they have. Mechanism design thus focuses on the study of solution concepts for a class of private-information games.
Mechanism design has broad applications, including traditional domains of economics such as market design, but also political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
(through voting theory). It is a foundational component in the operation of the internet
The Internet (or internet) is the Global network, global system of interconnected computer networks that uses the Internet protocol suite (TCP/IP) to communicate between networks and devices. It is a internetworking, network of networks ...
, being used in networked systems (such as inter-domain routing), e-commerce
E-commerce (electronic commerce) refers to commercial activities including the electronic buying or selling products and services which are conducted on online platforms or over the Internet. E-commerce draws on technologies such as mobile co ...
, and advertisement auctions by Facebook
Facebook is a social media and social networking service owned by the American technology conglomerate Meta Platforms, Meta. Created in 2004 by Mark Zuckerberg with four other Harvard College students and roommates, Eduardo Saverin, Andre ...
and Google
Google LLC (, ) is an American multinational corporation and technology company focusing on online advertising, search engine technology, cloud computing, computer software, quantum computing, e-commerce, consumer electronics, and artificial ...
.
Because it starts with the end of the game (a particular result), then works backwards to find a game that implements it, it is sometimes described as reverse game theory. Leonid Hurwicz explains that "in a design problem, the goal function is the main given, while the mechanism is the unknown. Therefore, the design problem is the inverse of traditional economic theory, which is typically devoted to the analysis of the performance of a given mechanism."
The 2007 Nobel Memorial Prize in Economic Sciences
The Nobel Memorial Prize in Economic Sciences, officially the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel (), commonly referred to as the Nobel Prize in Economics(), is an award in the field of economic sciences adminis ...
was awarded to Leonid Hurwicz, Eric Maskin, and Roger Myerson
Roger Bruce Myerson (born March 29, 1951) is an American economist and professor at the University of Chicago. He holds the title of the David L. Pearson Distinguished Service Professor of Global Conflict Studies at The Pearson Institute for the ...
"for having laid the foundations of mechanism design theory." The related works of William Vickrey that established the field earned him the 1996 Nobel prize.
Description
One person, called the "principal", would like to condition his behavior on information privately known to the players of agame
A game is a structured type of play usually undertaken for entertainment or fun, and sometimes used as an educational tool. Many games are also considered to be work (such as professional players of spectator sports or video games) or art ...
. For example, the principal would like to know the true quality of a used car a salesman is pitching. He cannot learn anything simply by asking the salesman, because it is in the salesman's interest to distort the truth. However, in mechanism design, the principal does have one advantage: He may design a game whose rules influence others to act the way he would like.
Without mechanism design theory, the principal's problem would be difficult to solve. He would have to consider all the possible games and choose the one that best influences other players' tactics. In addition, the principal would have to draw conclusions from agents who may lie to him. Thanks to the revelation principle, the principal only needs to consider games in which agents truthfully report their private information.
Foundations
Mechanism
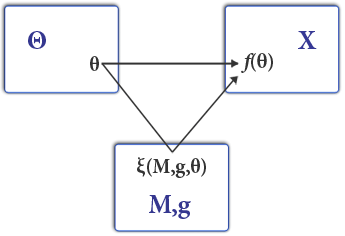
A game of mechanism design is a game of private information in which one of the agents, called the principal, chooses the payoff structure. Following , the agents receive secret "messages" from nature containing information relevant to payoffs. For example, a message may contain information about their preferences or the quality of a good for sale. We call this information the agent's "type" (usually noted and accordingly the space of types ). Agents then report a type to the principal (usually noted with a hat ) that can be a strategic lie. After the report, the principal and the agents are paid according to the payoff structure the principal chose. The timing of the game is: # The principal commits to a mechanism that grants an outcome as a function of reported type # The agents report, possibly dishonestly, a type profile # The mechanism is executed (agents receive outcome ) In order to understand who gets what, it is common to divide the outcome into a goods allocation and a money transfer, where stands for an allocation of goods rendered or received as a function of type, and stands for a monetary transfer as a function of type. As a benchmark the designer often defines what should happen under full information. Define a social choice function mapping the (true) type profile directly to the allocation of goods received or rendered, : In contrast a mechanism maps the ''reported'' type profile to an ''outcome'' (again, both a goods allocation and a money transfer ) :Revelation principle
A proposed mechanism constitutes a Bayesian game (a game of private information), and if it is well-behaved the game has a Bayesian Nash equilibrium. At equilibrium agents choose their reports strategically as a function of type : It is difficult to solve for Bayesian equilibria in such a setting because it involves solving for agents' best-response strategies and for the best inference from a possible strategic lie. Thanks to a sweeping result called the revelation principle, no matter the mechanism a designer can confine attention to equilibria in which agents truthfully report type. The revelation principle states: "To every Bayesian Nash equilibrium there corresponds a Bayesian game with the same equilibrium outcome but in which players truthfully report type." This is extremely useful. The principle allows one to solve for a Bayesian equilibrium by assuming all players truthfully report type (subject to an incentive compatibility constraint). In one blow it eliminates the need to consider either strategic behavior or lying. Its proof is quite direct. Assume a Bayesian game in which the agent's strategy and payoff are functions of its type and what others do, . By definition agent ''is equilibrium strategy is Nash in expected utility: : Simply define a mechanism that would induce agents to choose the same equilibrium. The easiest one to define is for the mechanism to commit to playing the agents' equilibrium strategies ''for'' them. : Under such a mechanism the agents of course find it optimal to reveal type since the mechanism plays the strategies they found optimal anyway. Formally, choose such that :Implementability
The designer of a mechanism generally hopes either * to design a mechanism that "implements" a social choice function * to find the mechanism that maximizes some value criterion (e.g. profit) To implement a social choice function is to find some transfer function that motivates agents to pick . Formally, if the equilibrium strategy profile under the mechanism maps to the same goods allocation as a social choice function, : we say the mechanism implements the social choice function. Thanks to the revelation principle, the designer can usually find a transfer function to implement a social choice by solving an associated truthtelling game. If agents find it optimal to truthfully report type, : we say such a mechanism is truthfully implementable. The task is then to solve for a truthfully implementable and impute this transfer function to the original game. An allocation is truthfully implementable if there exists a transfer function such that : which is also called the incentive compatibility (IC) constraint. In applications, the IC condition is the key to describing the shape of in any useful way. Under certain conditions it can even isolate the transfer function analytically. Additionally, a participation ( individual rationality) constraint is sometimes added if agents have the option of not playing.Necessity
Consider a setting in which all agents have a type-contingent utility function . Consider also a goods allocation that is vector-valued and size (which permits number of goods) and assume it is piecewise continuous with respect to its arguments. The function is implementable only if : whenever and and ''x'' is continuous at . This is a necessary condition and is derived from the first- and second-order conditions of the agent's optimization problem assuming truth-telling. Its meaning can be understood in two pieces. The first piece says the agent's marginal rate of substitution (MRS) increases as a function of the type, : In short, agents will not tell the truth if the mechanism does not offer higher agent types a better deal. Otherwise, higher types facing any mechanism that punishes high types for reporting will lie and declare they are lower types, violating the truthtelling incentive-compatibility constraint. The second piece is a monotonicity condition waiting to happen, : which, to be positive, means higher types must be given more of the good. There is potential for the two pieces to interact. If for some type range the contract offered less quantity to higher types , it is possible the mechanism could compensate by giving higher types a discount. But such a contract already exists for low-type agents, so this solution is pathological. Such a solution sometimes occurs in the process of solving for a mechanism. In these cases it must be " ironed". In a multiple-good environment it is also possible for the designer to reward the agent with more of one good to substitute for less of another (e.g.butter
Butter is a dairy product made from the fat and protein components of Churning (butter), churned cream. It is a semi-solid emulsion at room temperature, consisting of approximately 81% butterfat. It is used at room temperature as a spread (food ...
for margarine). Multiple-good mechanisms are an area of continuing research in mechanism design.
Sufficiency
Mechanism design papers usually make two assumptions to ensure implementability: This is known by several names: the single-crossing condition, the sorting condition and the Spence–Mirrlees condition. It means the utility function is of such a shape that the agent's MRS is increasing in type. This is a technical condition bounding the rate of growth of the MRS. These assumptions are sufficient to provide that any monotonic is implementable (a exists that can implement it). In addition, in the single-good setting the single-crossing condition is sufficient to provide that only a monotonic is implementable, so the designer can confine his search to a monotonic .Highlighted results
Revenue equivalence theorem
gives a celebrated result that any member of a large class of auctions assures the seller of the same expected revenue and that the expected revenue is the best the seller can do. This is the case if # The buyers have identical valuation functions (which may be a function of type) # The buyers' types are independently distributed # The buyers types are drawn from a continuous distribution # The type distribution bears the monotone hazard rate property # The mechanism sells the good to the buyer with the highest valuation The last condition is crucial to the theorem. An implication is that for the seller to achieve higher revenue he must take a chance on giving the item to an agent with a lower valuation. Usually this means he must risk not selling the item at all.Vickrey–Clarke–Groves mechanisms
The Vickrey (1961) auction model was later expanded by and Groves to treat a public choice problem in which a public project's cost is borne by all agents, e.g. whether to build a municipal bridge. The resulting "Vickrey–Clarke–Groves" mechanism can motivate agents to choose the socially efficient allocation of the public good even if agents have privately known valuations. In other words, it can solve the " tragedy of the commons"—under certain conditions, in particular quasilinear utility or if budget balance is not required. Consider a setting in which number of agents have quasilinear utility with private valuations where the currency is valued linearly. The VCG designer designs an incentive compatible (hence truthfully implementable) mechanism to obtain the true type profile, from which the designer implements the socially optimal allocation : The cleverness of the VCG mechanism is the way it motivates truthful revelation. It eliminates incentives to misreport by penalizing any agent by the cost of the distortion he causes. Among the reports the agent may make, the VCG mechanism permits a "null" report saying he is indifferent to the public good and cares only about the money transfer. This effectively removes the agent from the game. If an agent does choose to report a type, the VCG mechanism charges the agent a fee if his report is pivotal, that is if his report changes the optimal allocation ''x'' so as to harm other agents. The payment is calculated : which sums the distortion in the utilities of the other agents (and not his own) caused by one agent reporting.Gibbard–Satterthwaite theorem
and give an impossibility result similar in spirit to Arrow's impossibility theorem. For a very general class of games, only "dictatorial" social choice functions can be implemented. A social choice function is dictatorial if one agent always receives his most-favored goods allocation, : The theorem states that under general conditions any truthfully implementable social choice function must be dictatorial if, # ''X'' is finite and contains at least three elements # Preferences are rational #Myerson–Satterthwaite theorem
show there is no efficient way for two parties to trade a good when they each have secret and probabilistically varying valuations for it, without the risk of forcing one party to trade at a loss. It is among the most remarkable negative results in economics—a kind of negative mirror to the fundamental theorems of welfare economics.Shapley value
Phillips and Marden (2018) proved that for cost-sharing games with concave cost functions, the optimal cost-sharing rule that firstly optimizes the worst-case inefficiencies in a game (the price of anarchy), and then secondly optimizes the best-case outcomes (the price of stability), is precisely the Shapley value cost-sharing rule. A symmetrical statement is similarly valid for utility-sharing games with convex utility functions.Price discrimination
introduces a setting in which the transfer function ''t''() is easy to solve for. Due to its relevance and tractability it is a common setting in the literature. Consider a single-good, single-agent setting in which the agent has quasilinear utility with an unknown type parameter : and in which the principal has a prior CDF over the agent's type . The principal can produce goods at a convex marginal cost ''c''(''x'') and wants to maximize the expected profit from the transaction :