Maximum Power Theorem on:
[Wikipedia]
[Google]
[Amazon]
In
 The theorem was originally misunderstood (notably by Joule) to imply that a system consisting of an electric motor driven by a battery could not be more than 50% efficient, since the power dissipated as heat in the battery would always be equal to the power delivered to the motor when the impedances were matched.
In 1880 this assumption was shown to be false by either
The theorem was originally misunderstood (notably by Joule) to imply that a system consisting of an electric motor driven by a battery could not be more than 50% efficient, since the power dissipated as heat in the battery would always be equal to the power delivered to the motor when the impedances were matched.
In 1880 this assumption was shown to be false by either  The efficiency is the ratio of power dissipated by the load resistance to total power dissipated by circuit (which includes the voltage source's resistance of as well as ):
Consider three particular cases:
* If , then Efficiency approaches 0% if the load resistance approaches zero (a short circuit), since all power is consumed in the source and no power is consumed in the short. Note, voltage sources must have some resistance.
* If , then Efficiency is only 50% if the load resistance equals the source resistance (which is the condition of maximum power transfer).
* If , then Efficiency approaches 100% if the load resistance approaches infinity (though the total power level tends towards zero) or if the source resistance approaches zero. Using a large ratio is called impedance bridging.
The efficiency is the ratio of power dissipated by the load resistance to total power dissipated by circuit (which includes the voltage source's resistance of as well as ):
Consider three particular cases:
* If , then Efficiency approaches 0% if the load resistance approaches zero (a short circuit), since all power is consumed in the source and no power is consumed in the short. Note, voltage sources must have some resistance.
* If , then Efficiency is only 50% if the load resistance equals the source resistance (which is the condition of maximum power transfer).
* If , then Efficiency approaches 100% if the load resistance approaches infinity (though the total power level tends towards zero) or if the source resistance approaches zero. Using a large ratio is called impedance bridging.
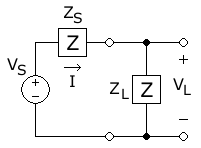 In this diagram, AC power is being transferred from the source, with
In this diagram, AC power is being transferred from the source, with
''Conjugate matching versus reflectionless matching''
(
''Electromagnetic Waves and Antennas''
Circuit theorems Electrical engineering
electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems which use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, the maximum power transfer theorem states that, to obtain ''maximum'' external power from a power source with internal resistance, the resistance
Resistance may refer to:
Arts, entertainment, and media Comics
* Either of two similarly named but otherwise unrelated comic book series, both published by Wildstorm:
** ''Resistance'' (comics), based on the video game of the same title
** ''T ...
of the load
Load or LOAD may refer to:
Aeronautics and transportation
*Load factor (aeronautics), the ratio of the lift of an aircraft to its weight
*Passenger load factor, the ratio of revenue passenger miles to available seat miles of a particular transpo ...
must equal the resistance of the source as viewed from its output terminals. Moritz von Jacobi published the maximum power (transfer) theorem around 1840; it is also referred to as "Jacobi's law".
The theorem results in maximum ''power'' transfer from the power source to the load, and not maximum ''efficiency
Efficiency is the often measurable ability to avoid wasting materials, energy, efforts, money, and time in doing something or in producing a desired result. In a more general sense, it is the ability to do things well, successfully, and without ...
'' of useful power out of total power consumed. If the load resistance is made larger than the source resistance, then efficiency increases (since a higher percentage of the source power is transferred to the load), but the ''magnitude'' of the load power decreases (since the total circuit resistance increases). If the load resistance is made smaller than the source resistance, then efficiency decreases (since most of the power ends up being dissipated in the source). Although the total power dissipated increases (due to a lower total resistance), the amount dissipated in the load decreases.
The theorem states how to choose (so as to maximize power transfer) the load resistance, once the source resistance is given. It is a common misconception to apply the theorem in the opposite scenario. It does ''not'' say how to choose the source resistance for a given load resistance. In fact, the source resistance that maximizes power transfer from a voltage source is always zero (the hypothetical ideal voltage source
A voltage source is a two-terminal device which can maintain a fixed voltage. An ideal voltage source can maintain the fixed voltage independent of the load resistance or the output current. However, a real-world voltage source cannot supply unli ...
), regardless of the value of the load resistance.
The theorem can be extended to alternating current circuits that include reactance, and states that maximum power transfer occurs when the load impedance is equal to the complex conjugate of the source impedance.
The mathematics of the theorem also applies to other physical interactions, such as:
* mechanical collisions between two objects,
* the sharing of charge between two capacitors,
* liquid flow between two cylinders,
* the transmission and reflection of light at the boundary between two media.
Maximizing power transfer versus power efficiency
Edison
Thomas Alva Edison (February 11, 1847October 18, 1931) was an American inventor and businessman. He developed many devices in fields such as electric power generation, mass communication, sound recording, and motion pictures. These invention ...
or his colleague Francis Robbins Upton, who realized that maximum efficiency was not the same as maximum power transfer.
To achieve maximum efficiency, the resistance of the source (whether a battery or a dynamo) could be (or should be) made as close to zero as possible. Using this new understanding, they obtained an efficiency of about 90%, and proved that the electric motor was a practical alternative to the heat engine.Impedance matching
A related concept is reflectionless impedance matching. In radio frequency transmission lines, and other electronics, there is often a requirement to match the source impedance (at the transmitter) to the load impedance (such as anantenna
Antenna ( antennas or antennae) may refer to:
Science and engineering
* Antenna (radio), also known as an aerial, a transducer designed to transmit or receive electromagnetic (e.g., TV or radio) waves
* Antennae Galaxies, the name of two collid ...
) to avoid reflections in the transmission line that could overload or damage the transmitter.
Calculus-based proof for purely resistive circuits
In the simplified model of powering a load with resistance by a source with voltage and source resistance , then byOhm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equat ...
the resulting current is simply the source voltage divided by the total circuit resistance:
The power dissipated in the load is the square of the current multiplied by the resistance:
The value of for which this expression is a maximum could be calculated by differentiating it, but it is easier to calculate the value of for which the denominator
is a minimum. The result will be the same in either case. Differentiating the denominator with respect to :
For a maximum or minimum, the first derivative is zero, so
or
In practical resistive circuits, and are both positive, so the positive sign in the above is the correct solution.
To find out whether this solution is a minimum or a maximum, the denominator expression is differentiated again:
This is always positive for positive values of and , showing that the denominator is a minimum, and the power is therefore a maximum, when
The above proof assumes fixed source resistance . When the source resistance can be varied, power transferred to the load can be increased by reducing . For example, a 100 Volt source with an of will deliver 250 watts of power to a load; reducing to increases the power delivered to 1000 watts.
Note that this shows that maximum power transfer can also be interpreted as the load voltage being equal to one-half of the Thevenin voltage equivalent of the source.
In reactive circuits
The power transfer theorem also applies when the source and/or load are not purely resistive. A refinement of the maximum power theorem says that any reactive components of source and load should be of equal magnitude but opposite sign. (''See below for a derivation.'') * This means that the source and load impedances should be '' complex conjugates'' of each other. * In the case of purely resistive circuits, the two concepts are identical. Physically realizable sources and loads are not usually purely resistive, having some inductive or capacitive components, and so practical applications of this theorem, under the name of complex conjugate impedance matching, do, in fact, exist. If the source is totally inductive (capacitive), then a totally capacitive (inductive) load, in the absence of resistive losses, would receive 100% of the energy from the source but send it back after a quarter cycle. The resultant circuit is nothing other than a resonantLC circuit
An LC circuit, also called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, represented by the letter L, and a capacitor, represented by the letter C, connected together. The circuit can ac ...
in which the energy continues to oscillate to and fro. This oscillation is called reactive power
Reactive may refer to:
*Generally, capable of having a reaction (disambiguation)
*An adjective abbreviation denoting a bowling ball coverstock made of reactive resin
*Reactivity (chemistry)
*Reactive mind
*Reactive programming
See also
*Reactanc ...
.
Power factor correction
In electrical engineering, the power factor of an AC power system is defined as the ratio of the '' real power'' absorbed by the load to the ''apparent power'' flowing in the circuit. Real power is the average of the instantaneous product of v ...
(where an inductive reactance is used to "balance out" a capacitive one), is essentially the same idea as complex conjugate impedance matching although it is done for entirely different reasons.
For a fixed reactive ''source'', the maximum power theorem maximizes the real power (P) delivered to the load by complex conjugate matching the load to the source.
For a fixed reactive ''load'', power factor correction minimizes the apparent power (S) (and unnecessary current) conducted by the transmission lines, while maintaining the same amount of real power transfer.
This is done by adding a reactance to the load to balance out the load's own reactance, changing the reactive load impedance into a resistive load impedance.
Proof
 In this diagram, AC power is being transferred from the source, with
In this diagram, AC power is being transferred from the source, with phasor
In physics and engineering, a phasor (a portmanteau of phase vector) is a complex number representing a sinusoidal function whose amplitude (''A''), angular frequency (''ω''), and initial phase (''θ'') are time-invariant. It is related to ...
magnitude of voltage (positive peak voltage) and fixed source impedance (S for source), to a load with impedance (L for load), resulting in a (positive) magnitude of the current phasor . This magnitude results from dividing the magnitude of the source voltage by the magnitude of the total circuit impedance:
The average power dissipated in the load is the square of the current multiplied by the resistive portion (the real part) of the load impedance :
where and denote the resistances, that is the real parts, and and denote the reactances, that is the imaginary parts, of respectively the source and load impedances and .
To determine, for a given source voltage and impedance the value of the load impedance for which this expression for the power yields a maximum, one first finds, for each fixed positive value of , the value of the reactive term for which the denominator
is a minimum. Since reactances can be negative, this is achieved by adapting the load reactance to
This reduces the above equation to:
and it remains to find the value of which maximizes this expression. This problem has the same form as in the purely resistive case, and the maximizing condition therefore is
The two maximizing conditions
*
*
describe the complex conjugate of the source impedance, denoted by and thus can be concisely combined to:
Notes
References
*H.W. Jackson (1959) Introduction to Electronic Circuits, Prentice-Hall.External links
''Conjugate matching versus reflectionless matching''
(
PDF
Portable Document Format (PDF), standardized as ISO 32000, is a file format developed by Adobe in 1992 to present documents, including text formatting and images, in a manner independent of application software, hardware, and operating systems. ...
) taken fro''Electromagnetic Waves and Antennas''
Circuit theorems Electrical engineering