Majority function on:
[Wikipedia]
[Google]
[Amazon]
In

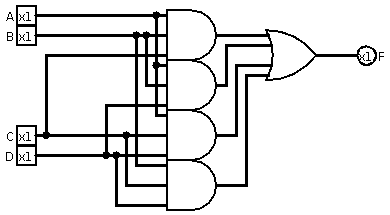 A ''majority gate'' is a logical gate used in
A ''majority gate'' is a logical gate used in
Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas in ...
, the majority function (also called the median operator) is the Boolean function
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually , or ). Alternative names are switching function, used especially in older computer science literature, and truth function ...
that evaluates to false when half or more arguments are false and true otherwise, i.e. the value of the function equals the value of the majority of the inputs. Representing true values as 1 and false values as 0, we may use the (real-valued) formula:
:
The "−1/2" in the formula serves to break ties in favor of zeros when the number of arguments ''n'' is even. If the term "−1/2" is omitted, the formula can be used for a function that breaks ties in favor of ones.
Most applications deliberately force an odd number of inputs so they don't have to deal with the question of what happens when exactly half the inputs are 0 and exactly half the inputs are 1. The few systems that calculate the majority function on an even number of inputs are often biased towards "0"—they produce "0" when exactly half the inputs are 0 -- for example, a 4-input majority gate has a 0 output only when two or more 0's appear at its inputs. In a few systems, the tie can be broken randomly.
Boolean circuits

 A ''majority gate'' is a logical gate used in
A ''majority gate'' is a logical gate used in circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the ci ...
and other applications of Boolean circuits
In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible inp ...
. A majority gate returns true if and only if more than 50% of its inputs are true.
For instance, in a full adder, the carry output is found by applying a majority function to the three inputs, although frequently this part of the adder is broken down into several simpler logical gates.
Many systems have triple modular redundancy
Triple is used in several contexts to mean "threefold" or a "treble":
Sports
* Triple (baseball), a three-base hit
* A basketball three-point field goal
* A figure skating jump with three rotations
* In bowling terms, three strikes in a row
* ...
; they use the majority function for majority logic decoding to implement error correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communic ...
.
A major result in circuit complexity
In theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of the Boolean circuits that compute them. A related notion is the ci ...
asserts that the majority function cannot be computed by AC0 circuits of subexponential size.
Properties
For any ''x'', ''y'', and ''z'', the ternary median operator ⟨''x'', ''y'', ''z''⟩ satisfies the following equations. * ⟨''x'', ''y'', ''y''⟩ = ''y'' * ⟨''x'', ''y'', ''z''⟩ = ⟨''z'', ''x'', ''y''⟩ * ⟨''x'', ''y'', ''z''⟩ = ⟨''x'', ''z'', ''y''⟩ * ⟨⟨''x'', ''w'', ''y''⟩, ''w'', ''z''⟩ = ⟨''x'', ''w'', ⟨''y'', ''w'', ''z''⟩⟩ An abstract system satisfying these as axioms is a median algebra.Monotone formulae for majority
For ''n'' = 1 the median operator is just the unary identity operation ''x''. For ''n'' = 3 the ternary median operator can be expressed using conjunction and disjunction as ''xy'' + ''yz'' + ''zx''. Remarkably this expression denotes the same operation independently of whether the symbol + is interpreted asinclusive or
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor ...
or exclusive or
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , ...
.
For an arbitrary ''n'' there exists a monotone formula for majority of size O(''n''5.3). This is proved using probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects fr ...
. Thus, this formula is non-constructive.
Approaches exist for an explicit formula for majority of polynomial size:
* Take the median from a sorting network, where each compare-and-swap "wire" is simply an OR gate and an AND gate. The Ajtai– Komlós– Szemerédi (AKS) construction is an example.
* Combine the outputs of smaller majority circuits.
* Derandomize the Valiant proof of a monotone formula.
Notes
References
*See also
{{Commonscat-inline, Majority functions * Boolean algebra (structure) * Boolean algebras canonically defined * Boyer–Moore majority vote algorithm *Majority problem (cellular automaton) The majority problem, or density classification task, is the problem of finding one-dimensional cellular automaton rules that accurately perform majority voting.
Using local transition rules, cells cannot know the total count of all the ones in s ...
Logic gates
Circuit complexity
Boolean algebra