Lotka's law, named after Alfred J. Lotka, is one of a variety of special applications of

Zipf's law Zipf's law (; ) is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the -th entry is often approximately inversely proportional to . The best known instance of Zipf's law applies to the ...

. It describes the frequency of publication by authors in any given field.

Definition

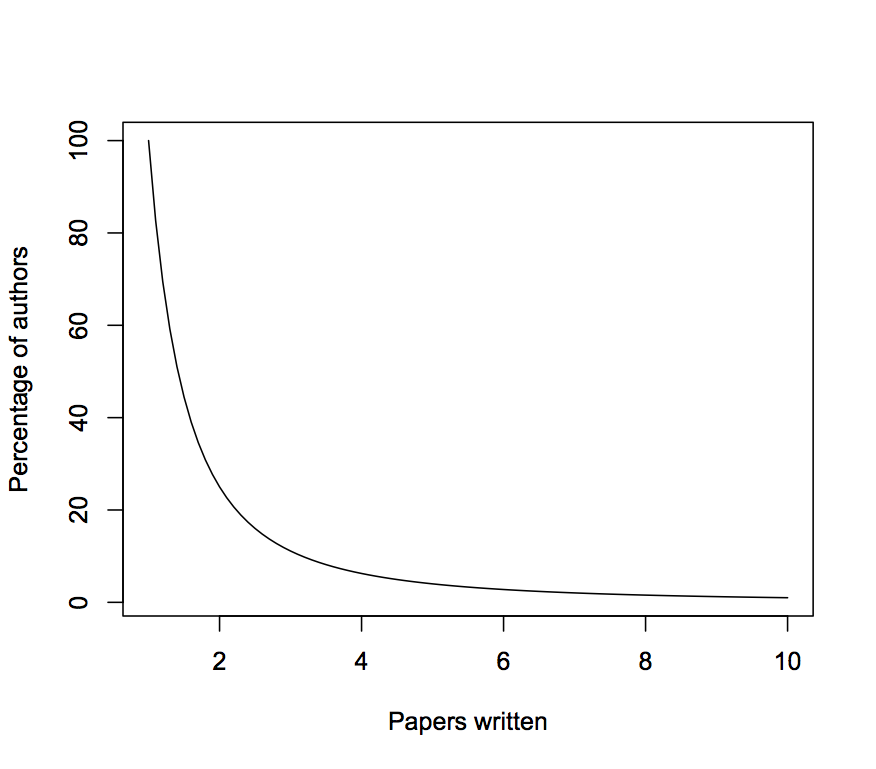
Let

X

be the number of publications,

Y

be the number of authors with

X

publications, and

k

be a constant depending on the specific field. Lotka's law states that

Y \propto X^

. In Lotka's original publication, he claimed

k=2

. Subsequent research showed that

k

varies depending on the discipline. Equivalently, Lotka's law can be stated as

Y' \propto X^

, where

Y'

is the number of authors with ''at least''

X

publications. Their equivalence can be proved by taking the

derivative In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...

Example

Assume that n=2 in a discipline, then as the number of articles published increases, authors producing that many publications become less frequent. There are 1/4 as many authors publishing two articles within a specified time period as there are single-publication authors, 1/9 as many publishing three articles, 1/16 as many publishing four articles, etc. And if 100 authors wrote ''exactly'' one article each over a specific period in the discipline, then: That would be a total of 294 articles and 155 writers, with an average of 1.9 articles for each writer.

Software

* Friedman, A. 2015. "The Power of Lotka’s Law Through the Eyes of R" The Romanian Statistical Review. Published b
National Institute of Statistics
*

to fit a Lotka power law distribution to observed frequency data.

Relationship to Riemann Zeta

Lotka's law may be described using the Zeta distribution: :

f(x) =  \frac \cdot \frac

for

x = 1, 2, 3, 4, \dots

and where :

\zeta (s) =  \sum_^\infty  \frac

is the

Riemann zeta function The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for and its analytic c ...

. It is the limiting case of

where an individual's maximum number of publications is infinite.

References

External links

*
''The Journal of the Washington Academy of Sciences'', vol. 16
{{DEFAULTSORT:Lotka's Law Bibliometrics Statistical laws