Liouville's Theorem (Hamiltonian)

In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics. It asserts that ''the phase-space distribution function is constant along the trajectories of the system''—that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time. This time-independent density is in statistical mechanics known as the classical a priori probability.

Liouville's theorem applies to conservative systems, that is, systems in which the effects of friction are absent or can be ignored. The general mathematical formulation for such systems is the measure-preserving dynamical system. Liouville's theorem applies when there are degrees of freedom that can be interpreted as positions and momenta; not all measure-preserving dynamical systems have these, but Hamiltonian systems do. The general setting for conjugate position and momentum coordinates is available in the mathematical setting of symplectic geometry. Liouville's theorem ignores the possibility of chemical reactions, where the total number of particles may change over time, or where energy may be transferred to internal degrees of freedom. The non-squeezing theorem, which applies to all symplectic maps (the Hamiltonian is a symplectic map) implies further restrictions on phase-space flows beyond volume/density/measure conservation. There are extensions of Liouville's theorem to cover these various generalized settings, including stochastic systems.

Liouville equation

The Liouville equation describes the time evolution of the ''phase space distribution function''. Although the equation is usually referred to as the "Liouville equation", Josiah Willard Gibbs was the first to recognize the importance of this equation as the fundamental equation of statistical mechanics. It is referred to as the Liouville equation because its derivation for non-canonical systems utilises an identity first derived by Liouville in 1838.

Consider a Hamiltonian dynamical system with canonical coordinates $q_i$ and conjugate momenta $p_i$, where $i=1,\dots,n$. Then the phase space distribution $\rho(p,q,t)$ determines the probability $\rho(p,q,t)\; \mathrm^nq\,\mathrm^n p$ that the system will be found in the infinitesimal phase space volume $\mathrm ^nq\,\mathrm^n p$ at time $t$. The Liouville equation is

$\frac + \sum_^n \left(\frac \dot_i +\frac \dot_i\right) = 0.$

Time derivatives are denoted by dots, and are evaluated according to Hamilton's equations for the system. This equation demonstrates the conservation of density in phase space (which was Gibbs's name for the theorem). Liouville's theorem states that:

A proof of Liouville's theorem uses the ''n''-dimensional divergence theorem. The proof is based on the fact that the evolution of $\rho$ obeys an ''2n''-dimensional version of the continuity equation:

$\frac + \vec \nabla \cdot (\rho \vec u) = 0$

with $\vec u = (\dot_1, \dot_2, \dots, \dot_n, \dot_1,\dot_2,...,\dot_n )$ being the "velocity" vector of $p_i$ and $q_i$. The above equation means that change of the total probability within a small volume in phase space is equal to the net flux of probability density into or out of the volume. After inserting $\vec u$ in the above equation, we reach

$\frac+\sum_^n\left(\frac+\frac\right)=0.$

That is, the 3-tuple $(\rho, \rho\dot_i,\rho\dot_i)$ is a conserved current. The above equation can be reduced to the Liouville equation based on the following identity

$\rho\sum_^n \left(\frac + \frac\right) = \rho\sum_^n \left(\frac - \frac\right)=0,$

where $H$ is the Hamiltonian, and we have used the relationships $\dot_i = \partial H / \partial p_i$ and $\dot_i = - \partial H / \partial$. The derivation of the Liouville equation can be viewed as the motion through phase space as a 'fluid flow' of system points. The theorem that the convective derivative of the density, $d \rho/dt$, is zero follows from the equation of continuity by noting that the 'velocity field' $(\dot p , \dot q)$ in phase space has zero divergence (which follows from Hamilton's relations).

Other formulations

Poisson bracket

The theorem above is often restated in terms of the Poisson bracket as
$\frac = \$
or, in terms of the linear Liouville operator or Liouvillian,
\mathrm\widehat=\sum_^n \left frac\frac-\frac\frac\right-\
as
$\frac+\rho =0.$

Ergodic theory

In ergodic theory and dynamical systems, motivated by the physical considerations given so far, there is a corresponding result also referred to as Liouville's theorem. In Hamiltonian mechanics, the phase space is a smooth manifold that comes naturally equipped with a smooth measure (locally, this measure is the 6''n''-dimensional Lebesgue measure). The theorem says this smooth measure is invariant under the Hamiltonian flow. More generally, one can describe the necessary and sufficient condition under which a smooth measure is invariant under a flow. The Hamiltonian case then becomes a corollary.

Symplectic geometry

We can also formulate Liouville's Theorem in terms of symplectic geometry. For a given system, we can consider the phase space $(q^\mu, p_\mu)$ of a particular Hamiltonian $H$ as a manifold $(M,\omega)$ endowed with a symplectic 2-form

$\omega = dp_\mu\wedge dq^\mu.$
The volume form of our manifold is the top exterior power of the symplectic 2-form, and is just another representation of the measure on the phase space described above.

On our phase space symplectic manifold we can define a Hamiltonian vector field generated by a function $f(q,p)$ as

$X_f = \frac\frac - \frac\frac.$

Specifically, when the generating function is the Hamiltonian itself, $f(q,p) = H$, we get

$X_H = \frac\frac - \frac\frac = \frac\frac + \frac\frac = \frac$

where we utilized Hamilton's equations of motion and the definition of the chain rule.

In this formalism, Liouville's Theorem states that the Lie derivative of the volume form is zero along the flow generated by $X_H$. That is, for $(M,\omega)$ a 2n-dimensional symplectic manifold,

$\mathcal_(\omega^n) = 0.$

In fact, the symplectic structure $\omega$ itself is preserved, not only its top exterior power. That is, Liouville's Theorem also gives Proves Liouville's theorem using the language of modern differential geometry.

$\mathcal_(\omega) = 0.$

Quantum Liouville equation

The analog of Liouville equation in quantum mechanics describes the time evolution of a mixed state. Canonical quantization yields a quantum-mechanical version of this theorem, the von Neumann equation. This procedure, often used to devise quantum analogues of classical systems, involves describing a classical system using Hamiltonian mechanics. Classical variables are then re-interpreted as quantum operators, while Poisson brackets are replaced by commutators. In this case, the resulting equation is
\frac = \frac , \rho
where ρ is the density matrix.

When applied to the expectation value of an observable, the corresponding equation is given by Ehrenfest's theorem, and takes the form

$\frac\langle A\rangle = -\frac\langle$, Arangle,

where $A$ is an observable. Note the sign difference, which follows from the assumption that the operator is stationary and the state is time-dependent.

In the phase-space formulation of quantum mechanics, substituting the Moyal brackets for Poisson brackets in the phase-space analog of the von Neumann equation results in compressibility of the probability fluid, and thus violations of Liouville's theorem incompressibility. This, then, leads to concomitant difficulties in defining meaningful quantum trajectories.

Examples

Simple harmonic oscillator phase-space volume

Consider an $N$-particle system in three dimensions, and focus on only the evolution of $\mathrm\mathcal$ particles. Within phase space, these $\mathrm\mathcal$ particles occupy an infinitesimal volume given by

$\mathrm\Gamma = \displaystyle\prod_^N d^3p_i d^3q_i.$

We want $\frac$ to remain the same throughout time, so that $\rho(\Gamma, t)$ is constant along the trajectories of the system. If we allow our particles to evolve by an infinitesimal time step $\delta t$, we see that each particle phase space location changes as

$\begin q_i' = q_i + \dot\delta t,\\ p_i' = p_i + \dot\delta t, \end$

where $\dot$ and $\dot$ denote $\frac$ and $\frac$ respectively, and we have only kept terms linear in $\delta t$. Extending this to our infinitesimal hypercube $\mathrm\Gamma$, the side lengths change as

\begin
dq_i' = dq_i + \tfrac dq_i \delta t,\\ ptdp_i' = dp_i + \tfrac dp_i \delta t.
\end

To find the new infinitesimal phase-space volume $\mathrm\Gamma'$, we need the product of the above quantities. To first order in $\delta t$, we get the following:

dq_i' dp_i' = dq_i dp_i \left + \left( \frac + \frac\right) \delta t\right

So far, we have yet to make any specifications about our system. Let us now specialize to the case of $N$ $3$-dimensional isotropic harmonic oscillators. That is, each particle in our ensemble can be treated as a simple harmonic oscillator. The Hamiltonian for this system is given by

$H = \sum_^\left(\fracp_i^2 + \fracq_i^2\right).$

By using Hamilton's equations with the above Hamiltonian we find that the term in parentheses above is identically zero, thus yielding

$dq_i' dp_i' = dq_i dp_i.$

From this we can find the infinitesimal volume of phase space:

$\mathrm\Gamma' = \prod_^N d^3q_i'd^3p_i' = \prod_^N d^3q_i d^3p_i = \mathrm\Gamma.$

Thus we have ultimately found that the infinitesimal phase-space volume is unchanged, yielding

$\rho(\Gamma', t + \delta t) = \frac = \frac = \rho(\Gamma, t),$

demonstrating that Liouville's theorem holds for this system.

The question remains of how the phase-space volume actually evolves in time. Above we have shown that the total volume is conserved, but said nothing about what it looks like. For a single particle we can see that its trajectory in phase space is given by the ellipse of constant $H$. Explicitly, one can solve Hamilton's equations for the system and find

$\begin q_i(t) &= Q_i\cos + \frac\sin,\\ p_i(t) &= P_i\cos - m\omega Q_i\sin, \end$

where $Q_i$ and $P_i$ denote the initial position and momentum of the $i$-th particle.
For a system of multiple particles, each one will have a phase-space trajectory that traces out an ellipse corresponding to the particle's energy. The frequency at which the ellipse is traced is given by the $\omega$ in the Hamiltonian, independent of any differences in energy. As a result, a region of phase space will simply rotate about the point $(\mathbf, \mathbf) = (0, 0)$ with frequency dependent on $\omega$. This can be seen in the animation above.

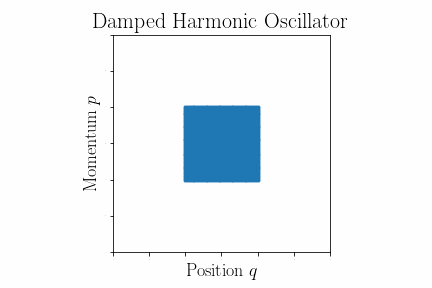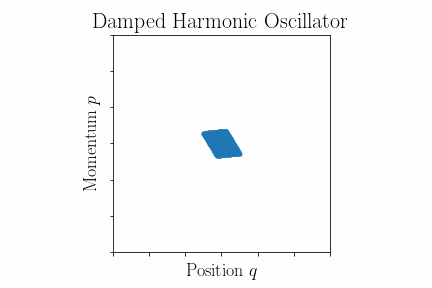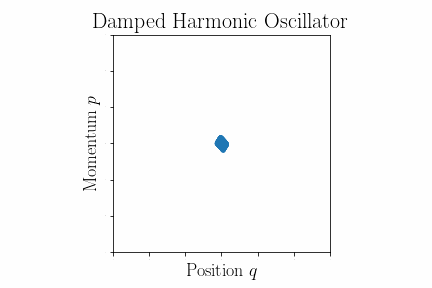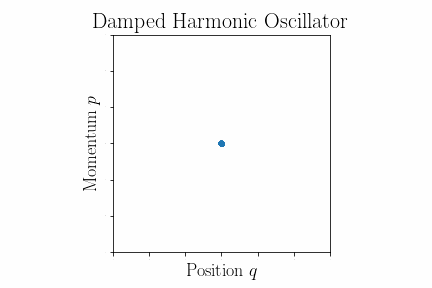
Damped harmonic oscillator

To see an example where Liouville's theorem does ''not'' apply, we can modify the equations of motion for the simple harmonic oscillator to account for the effects of friction or damping. Consider again the system of $N$ particles each in a $3$-dimensional isotropic harmonic potential, the Hamiltonian for which is given in the previous example. This time, we add the condition that each particle experiences a frictional force $-\gamma p_i$, where $\gamma$ is a positive constant dictating the amount of friction. As this is a non-conservative force, we need to extend Hamilton's equations as

\begin
\dot &= \hphantom\frac, \\ pt\dot &= -\frac - \gamma p_i.
\end

Unlike the equations of motion for the simple harmonic oscillator, these modified equations do not take the form of Hamilton's equations, and therefore we do not expect Liouville's theorem to hold. Instead, as depicted in the animation in this section, a generic phase space volume will shrink as it evolves under these equations of motion.

To see this violation of Liouville's theorem explicitly, we can follow a very similar procedure to the undamped harmonic oscillator case, and we arrive again at

dq_i' dp_i' = dq_i dp_i\left + \left( \frac + \frac\right) \delta t\right

Plugging in our modified Hamilton's equations, we find

\begin
dq_i' dp_i' &= dq_i dp_i\left + \left( \frac - \frac - \gamma\right) \delta t\right \\ ex&= dq_i dp_i\left -\gamma \delta t\right
\end

Calculating our new infinitesimal phase space volume, and keeping only first order in $\delta t$ we find the following result:

\mathrm\Gamma' = \prod_^N d^3q_i' d^3p_i' = \left - \gamma\delta t\right \prod_^N d^3q_i d^3p_i = \mathrm\Gamma \left - 3N\gamma\delta t\right

We have found that the infinitesimal phase-space volume is no longer constant, and thus the phase-space density is not conserved. As can be seen from the equation as time increases, we expect our phase-space volume to decrease to zero as friction affects the system.

As for how the phase-space volume evolves in time, we will still have the constant rotation as in the undamped case. However, the damping will introduce a steady decrease in the radii of each ellipse. Again we can solve for the trajectories explicitly using Hamilton's equations, taking care to use the modified ones above. Letting $\alpha \equiv /$ for convenience, we find

\begin
q_i(t) &= e^ \left _i\cos + B_i\sin\right& &\omega_1 \equiv \sqrt, \\ exp_i(t) &= e^ \left _i\cos - m(\omega_1 Q_i + 2\alpha B_i)\sin\right& &B_i \equiv \frac\left(\frac + 2\alpha Q_i\right),
\end

where the values $Q_i$ and $P_i$ denote the initial position and momentum of the $i$-th particle.
As the system evolves the total phase-space volume will spiral in to the origin. This can be seen in the figure above.

Remarks

* The Liouville equation is valid for both equilibrium and nonequilibrium systems. It is a fundamental equation of non-equilibrium statistical mechanics.
* The Liouville equation is integral to the proof of the fluctuation theorem from which the second law of thermodynamics can be derived. It is also the key component of the derivation of Green–Kubo relations for linear transport coefficients such as shear viscosity, thermal conductivity or electrical conductivity.
* Virtually any textbook on Hamiltonian mechanics, advanced statistical mechanics, or symplectic geometry will derive the Liouville theorem. Uses the ''n''-dimensional divergence theorem (without proof).
* In plasma physics, the Vlasov equation can be interpreted as Liouville's theorem, which reduces the task of solving the Vlasov equation to that of single particle motion.Schwartz, S. J., Daly, P. W., and Fazakerley, A. N., 1998, Multi-Spacecraft Analysis of Plasma Kinetics, in ''Analysis Methods for Multi-Spacecraft Data'', edited by G. Paschmann and P. W. Daly, no. SR-001 in ISSI Scientific Reports, chap. 7, pp. 159–163, ESA Publ. Div., Noordwijk, Netherlands. By using Liouville's theorem in this way with energy or magnetic moment conservation, for example, one can determine unknown fields using known particle distribution functions, or vice versa. This method is known as Liouville mapping.

See also

* Boltzmann transport equation
* Reversible reference system propagation algorithm (r-RESPA)

References

Further reading

*
*

External links

*{{cite web , title=Phase space distribution functions and Liouville's theorem , url=https://www.nyu.edu/classes/tuckerman/stat.mech/lectures/lecture_1/node7.html

Eponymous theorems of physics
Hamiltonian mechanics
Theorems in dynamical systems
Statistical mechanics theorems