Kempe's universality theorem on:
[Wikipedia]
[Google]
[Amazon]
In 1876 Alfred B. Kempe published his article ''On a General Method of describing Plane Curves of the nth degree by Linkwork,'' which showed that for an arbitrary algebraic plane curve a linkage can be constructed that draws the curve. This direct connection between linkages and J. Malkevich, Feature Column, American Mathematical Society.
/ref> Kempe recognized that his results demonstrate the existence of a drawing linkage but it would not be practical. He states
Automated Generation of Kempe Linkages for Algebraic Curves in a Dynamic Geometry System.
Saarland University, Saarbrucken, Germany, Faculty of Natural Sciences and Technology I, Department of Computer Science.
/ref> This has been extended to provide movement of the end-effector, but again for parameterized curves. M. Gallet, C. Koutschan, Z. Li, G. Regensburger, J. Schicho, and N. Villamiza (2017), Planar Linkages Following a Prescribed Motion
Mathematics of Computation, 86(303), pages 473-506. Specializing the curves to those defined by
J of Mechanisms and Robotics, 9(2), 024503 Bezier curves can be written in the form of
J of Computers and Information in Science and Engineering, 17(3)
(left) and the hypocycloid curve (right). Usin
SageMath
their design was interpreted into these images. The source code can be found o
GitHub

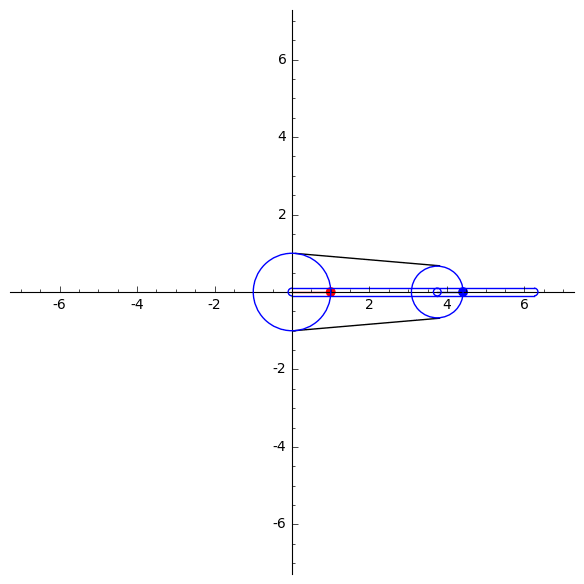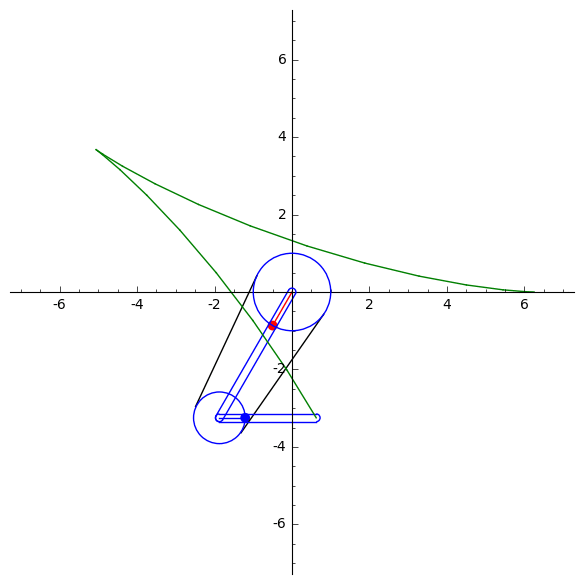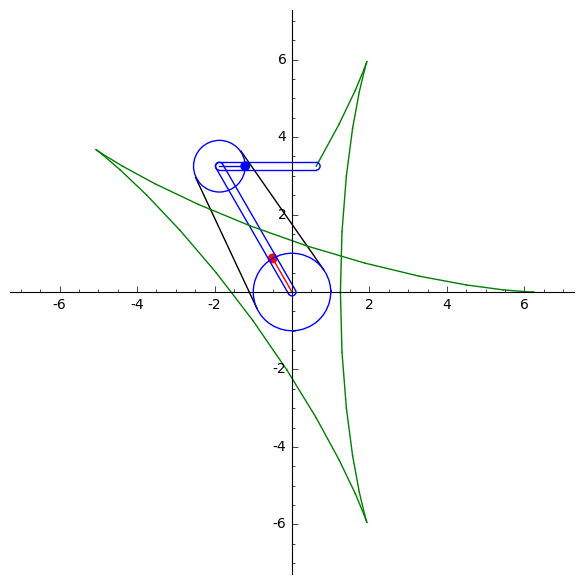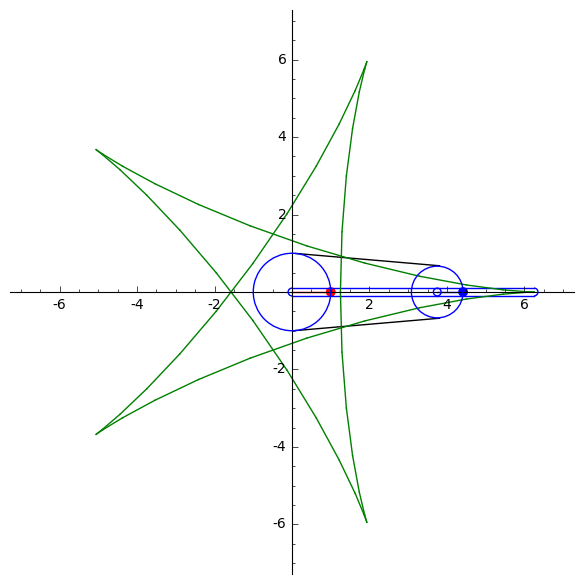
A. Kobel's animations of the parabola, self-intersecting cubic, smooth elliptic cubic and the trifolium curvesY. Liu's mechanical computation for drawing algebraic plane curvesM. Gallet et al. animations of linkages following a prescribed motionY. Liu's animations drawing trigonometric plane curves, the Butterfly mechanismLinkage that signs your nameLinkage that writes cursive Chinese
Linkages (mechanical)
algebraic curves
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane ...
has been named Kempe's universality theorem that any bounded subset of an algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane ...
may be traced out by the motion of one of the joints in a suitably chosen linkage. Kempe's proof was flawed and the first complete proof was provided in 2002 based on his ideas.
This theorem has been popularized by describing it as saying, "One can design a linkage which will sign your name!"/ref> Kempe recognized that his results demonstrate the existence of a drawing linkage but it would not be practical. He states
It is hardly necessary to add, that this method would not be practically useful on account of the complexity of the linkwork employed, a necessary consequence of the perfect generality of the demonstration.He then calls for the "mathematical artist" to find simpler ways to achieve this result:
The method has, however, an interest, as showing that there ''is'' a way of drawing any given case; and the variety of methods of expressing particular functions that have already been discovered renders it in the highest degree probable that in every case a simpler method can be found. There is still, however, a wide field open to the mathematical artist to discover the simplest linkworks that will describe particular curves.A series of animations demonstrating the linkwork that results from Kempe's universality theorem are available for the parabola, self-intersecting cubic, smooth elliptic cubic and the trifolium curves.A. Kobel, (2008
Automated Generation of Kempe Linkages for Algebraic Curves in a Dynamic Geometry System.
Saarland University, Saarbrucken, Germany, Faculty of Natural Sciences and Technology I, Department of Computer Science.
Simpler drawing linkages
Several approaches have been taken to simplify the drawing linkages that result from Kempe's universality theorem. Some of the complexity arises from the linkages Kempe used to perform addition and subtraction of two angles, the multiplication of an angle by a constant, and translation of the rotation of a link in one location to a rotation of a second link at another location. Kempe called these linkages additor, reversor, multiplicator and translator linkages, respectively. The drawing linkage can be simplified by using bevel gear differentials to add and subtract angles,gear train
A gear train is a mechanical system formed by mounting gears on a frame so the teeth of the gears engage.
Gear teeth are designed to ensure the pitch circles of engaging gears roll on each other without slipping, providing a smooth transmission ...
s to multiply angles and belt or cable drives to translate rotation angles.
Another source of complexity is the generality of Kempe's application to all algebraic curves. By focusing on parameterized algebraic curves, dual quaternion algebra can be used to factor the motion polynomial and obtain a drawing linkage.G.Hegedus, Z. Li, J. Schicho, H. P. Schrocker (2015), From the Fundamental Theorem of Algebra to Kempe’s Universality Theorem/ref> This has been extended to provide movement of the end-effector, but again for parameterized curves. M. Gallet, C. Koutschan, Z. Li, G. Regensburger, J. Schicho, and N. Villamiza (2017), Planar Linkages Following a Prescribed Motion
Mathematics of Computation, 86(303), pages 473-506. Specializing the curves to those defined by
trigonometric polynomial In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(''nx'') and cos(''nx'') with ''n'' taking on the values of one or more natural numbers. The c ...
s has provided another way to obtain simpler drawing linkages.Y. Liu and J. M. McCarthy (2017), Design of Mechanisms to Draw Trigonometric Plane CurvesJ of Mechanisms and Robotics, 9(2), 024503 Bezier curves can be written in the form of
trigonometric polynomial In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(''nx'') and cos(''nx'') with ''n'' taking on the values of one or more natural numbers. The c ...
s therefore a linkage system can be designed that draws any curve that is approximated by a sequence of Bezier curves.Y. Liu and J. M. McCarthy (2017), Design of a Linkage System to Write in CursiveJ of Computers and Information in Science and Engineering, 17(3)
Visualizations
Below is an example of a single-coupled serial chain mechanism, designed by Liu and McCarthy, used to draw th(left) and the hypocycloid curve (right). Usin
SageMath
their design was interpreted into these images. The source code can be found o
GitHub

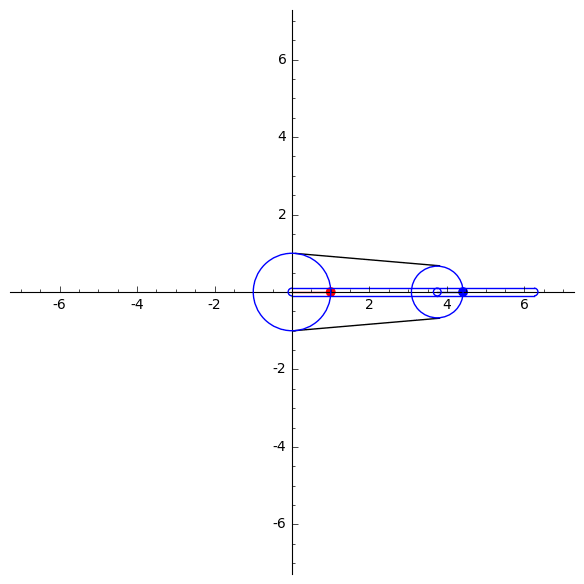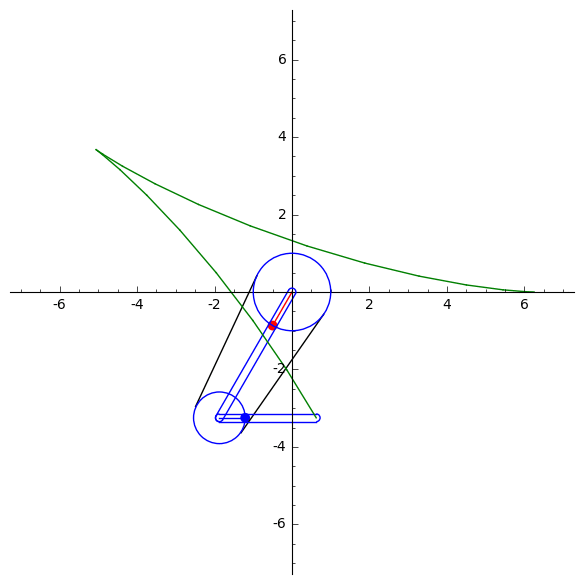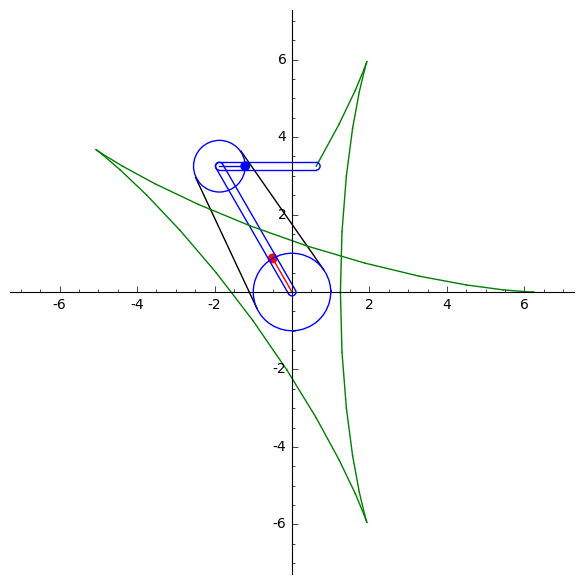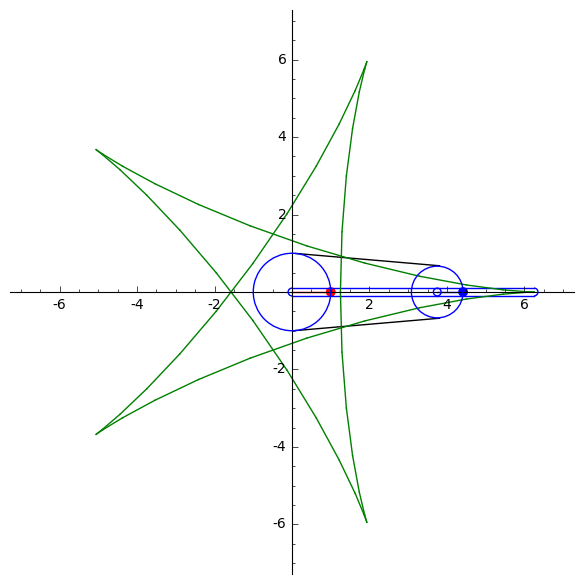
See also
*Structural rigidity
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.
Definitions
Rigidity is the property of a structu ...
References
{{reflistExternal links
A. Kobel's animations of the parabola, self-intersecting cubic, smooth elliptic cubic and the trifolium curves
Linkages (mechanical)