Joule–Thomson effect on:
[Wikipedia]
[Google]
[Amazon]
In
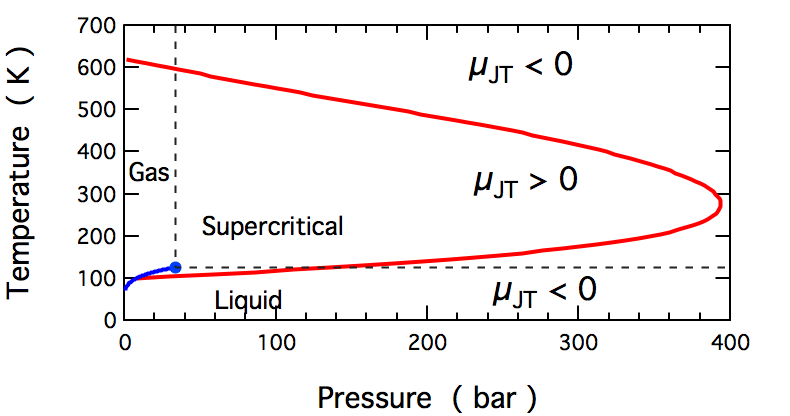 The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N2, are shown in the figure. Note that most conditions in the figure correspond to N2 being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N2) occurs as zero pressure is approached. For N2 gas at low pressures, is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N2 condenses to form a liquid and the coefficient again becomes negative. Thus, for N2 gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N2 forms.
The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N2, are shown in the figure. Note that most conditions in the figure correspond to N2 being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N2) occurs as zero pressure is approached. For N2 gas at low pressures, is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N2 condenses to form a liquid and the coefficient again becomes negative. Thus, for N2 gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N2 forms.
 The rate of change of temperature with respect to pressure in a Joule–Thomson process (that is, at constant enthalpy ) is the ''Joule–Thomson (Kelvin) coefficient'' . This coefficient can be expressed in terms of the gas's specific volume , its heat capacity at constant pressure , and its coefficient of thermal expansion as:
:
See the below for the proof of this relation. The value of is typically expressed in °C/ bar (SI units: K/ Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.
All real gases have an ''inversion point'' at which the value of changes sign. The temperature of this point, the ''Joule–Thomson inversion temperature'', depends on the pressure of the gas before expansion.
In a gas expansion the pressure decreases, so the sign of is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
The rate of change of temperature with respect to pressure in a Joule–Thomson process (that is, at constant enthalpy ) is the ''Joule–Thomson (Kelvin) coefficient'' . This coefficient can be expressed in terms of the gas's specific volume , its heat capacity at constant pressure , and its coefficient of thermal expansion as:
:
See the below for the proof of this relation. The value of is typically expressed in °C/ bar (SI units: K/ Pa) and depends on the type of gas and on the temperature and pressure of the gas before expansion. Its pressure dependence is usually only a few percent for pressures up to 100 bar.
All real gases have an ''inversion point'' at which the value of changes sign. The temperature of this point, the ''Joule–Thomson inversion temperature'', depends on the pressure of the gas before expansion.
In a gas expansion the pressure decreases, so the sign of is negative by definition. With that in mind, the following table explains when the Joule–Thomson effect cools or warms a real gas:
 For a Van der Waals gas, the coefficient iswith inversion temperature .
For the Dieterici gas, the reduced inversion temperature is , and the relation between reduced pressure and reduced inversion temperature is . This is plotted on the right. The critical point falls inside the region where the gas cools on expansion. The outside region is where the gas warms on expansion.
For a Van der Waals gas, the coefficient iswith inversion temperature .
For the Dieterici gas, the reduced inversion temperature is , and the relation between reduced pressure and reduced inversion temperature is . This is plotted on the right. The critical point falls inside the region where the gas cools on expansion. The outside region is where the gas warms on expansion.
 A convenient way to get a quantitative understanding of the throttling process is by using diagrams such as ''h''-''T'' diagrams, ''h''-''P'' diagrams, and others. Commonly used are the so-called ''T''-''s'' diagrams. Figure 2 shows the ''T''-''s'' diagram of nitrogen as an example. Various points are indicated as follows:
As shown before, throttling keeps ''h'' constant. E.g. throttling from 200 bar and 300K (point a in fig. 2) follows the isenthalpic (line of constant specific enthalpy) of 430kJ/kg. At 1 bar it results in point b which has a temperature of 270K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2K. Since the enthalpy is an extensive parameter the enthalpy in d (''h''d) is equal to the enthalpy in e (''h''e) multiplied with the mass fraction of the liquid in d (''x''d) plus the enthalpy in f (''h''f) multiplied with the mass fraction of the gas in d (1 − ''x''d). So
:
With numbers: 150 = ''x''d 28 + (1 − ''x''d) 230 so ''x''d is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.
A convenient way to get a quantitative understanding of the throttling process is by using diagrams such as ''h''-''T'' diagrams, ''h''-''P'' diagrams, and others. Commonly used are the so-called ''T''-''s'' diagrams. Figure 2 shows the ''T''-''s'' diagram of nitrogen as an example. Various points are indicated as follows:
As shown before, throttling keeps ''h'' constant. E.g. throttling from 200 bar and 300K (point a in fig. 2) follows the isenthalpic (line of constant specific enthalpy) of 430kJ/kg. At 1 bar it results in point b which has a temperature of 270K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2K. Since the enthalpy is an extensive parameter the enthalpy in d (''h''d) is equal to the enthalpy in e (''h''e) multiplied with the mass fraction of the liquid in d (''x''d) plus the enthalpy in f (''h''f) multiplied with the mass fraction of the gas in d (1 − ''x''d). So
:
With numbers: 150 = ''x''d 28 + (1 − ''x''d) 230 so ''x''d is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.
Joule–Thomson effect module
University of Notre Dame {{DEFAULTSORT:Joule-Thomson effect Thermodynamics Cryogenics Engineering thermodynamics Gases Heating, ventilation, and air conditioning Thomson effect William Thomson, 1st Baron Kelvin
thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
, the Joule–Thomson effect (also known as the Joule–Kelvin effect or Kelvin–Joule effect) describes the temperature change of a ''real'' gas or liquid
Liquid is a state of matter with a definite volume but no fixed shape. Liquids adapt to the shape of their container and are nearly incompressible, maintaining their volume even under pressure. The density of a liquid is usually close to th ...
(as differentiated from an ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
) when it is expanding; typically caused by the pressure loss from flow through a valve
A valve is a device or natural object that regulates, directs or controls the flow of a fluid (gases, liquids, fluidized solids, or Slurry, slurries) by opening, closing, or partially obstructing various passageways. Valves are technically Pip ...
or porous plug while keeping it insulated so that no heat is exchanged with the environment.
This procedure is called a ''throttling process'' or ''Joule–Thomson process''. The effect is purely due to deviation from ideality, as any ideal gas has no JT effect.
At room temperature, all gases except hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
, helium
Helium (from ) is a chemical element; it has chemical symbol, symbol He and atomic number 2. It is a colorless, odorless, non-toxic, inert gas, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling point is ...
, and neon
Neon is a chemical element; it has symbol Ne and atomic number 10. It is the second noble gas in the periodic table. Neon is a colorless, odorless, inert monatomic gas under standard conditions, with approximately two-thirds the density of ...
cool upon expansion by the Joule–Thomson process when being throttle
A throttle is a mechanism by which fluid flow is managed by construction or obstruction.
An engine's power can be increased or decreased by the restriction of inlet gases (by the use of a throttle), but usually decreased. The term ''throttle'' ha ...
d through an orifice; these three gases rise in temperature when forced through a porous plug at room temperature, but lowers in temperature when already at lower temperatures. Most liquids such as hydraulic
Hydraulics () is a technology and applied science using engineering, chemistry, and other sciences involving the mechanical properties and use of liquids. At a very basic level, hydraulics is the liquid counterpart of pneumatics, which concer ...
oils will be warmed by the Joule–Thomson throttling process. The temperature at which the JT effect switches sign is the inversion temperature.
The gas-cooling throttling process is commonly exploited in refrigeration processes such as liquefiers in air separation industrial process. In hydraulics, the warming effect from Joule–Thomson throttling can be used to find internally leaking valves as these will produce heat which can be detected by thermocouple
A thermocouple, also known as a "thermoelectrical thermometer", is an electrical device consisting of two dissimilar electrical conductors forming an electrical junction. A thermocouple produces a temperature-dependent voltage as a result of the ...
or thermal-imaging camera. Throttling is a fundamentally irreversible process
In thermodynamics, an irreversible process is a thermodynamic processes, process that cannot be undone. All complex natural processes are irreversible, although a phase transition at the coexistence temperature (e.g. melting of ice cubes in wate ...
. The throttling due to the flow resistance in supply lines, heat exchangers, regenerators, and other components of (thermal) machines is a source of losses that limits their performance.
Since it is a constant-enthalpy process, it can be used to experimentally measure the lines of constant enthalpy (isenthalps) on the diagram of a gas. Combined with the specific heat capacity ''at constant pressure'' it allows the complete measurement of the thermodynamic potential
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
for the gas.
History
The effect is named after James Prescott Joule andWilliam Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin (26 June 182417 December 1907), was a British mathematician, Mathematical physics, mathematical physicist and engineer. Born in Belfast, he was the Professor of Natural Philosophy (Glasgow), professor of Natur ...
, who discovered it in 1852. It followed upon earlier work by Joule on Joule expansion, in which a gas undergoes free expansion in a vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
and the temperature is unchanged, if the gas is ideal.
Description
The '' adiabatic'' (no heat exchanged) expansion of a gas may be carried out in a number of ways. The change in temperature experienced by the gas during expansion depends not only on the initial and final pressure, but also on the manner in which the expansion is carried out. *If the expansion process is reversible, meaning that the gas is inthermodynamic equilibrium
Thermodynamic equilibrium is a notion of thermodynamics with axiomatic status referring to an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable ...
at all times, it is called an ''isentropic
An isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in eng ...
'' expansion. In this scenario, the gas does positive work
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an ani ...
during the expansion, and its temperature decreases.
*In a free expansion, on the other hand, the gas does no work and absorbs no heat, so the internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
is conserved. Expanded in this manner, the temperature of an ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
would remain constant, but the temperature of a real gas decreases, except at very high temperature.
*The method of expansion discussed in this article, in which a gas or liquid at pressure ''P''1 flows into a region of lower pressure ''P''2 without significant change in kinetic energy, is called the Joule–Thomson expansion. The expansion is inherently irreversible. During this expansion, enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant extern ...
remains unchanged (see proof
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
below). Unlike a free expansion, work is done, causing a change in internal energy. Whether the internal energy increases or decreases is determined by whether work is done on or by the fluid; that is determined by the initial and final states of the expansion and the properties of the fluid.
 The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N2, are shown in the figure. Note that most conditions in the figure correspond to N2 being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N2) occurs as zero pressure is approached. For N2 gas at low pressures, is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N2 condenses to form a liquid and the coefficient again becomes negative. Thus, for N2 gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N2 forms.
The temperature change produced during a Joule–Thomson expansion is quantified by the Joule–Thomson coefficient, . This coefficient may be either positive (corresponding to cooling) or negative (heating); the regions where each occurs for molecular nitrogen, N2, are shown in the figure. Note that most conditions in the figure correspond to N2 being a supercritical fluid, where it has some properties of a gas and some of a liquid, but can not be really described as being either. The coefficient is negative at both very high and very low temperatures; at very high pressure it is negative at all temperatures. The maximum inversion temperature (621 K for N2) occurs as zero pressure is approached. For N2 gas at low pressures, is negative at high temperatures and positive at low temperatures. At temperatures below the gas-liquid coexistence curve, N2 condenses to form a liquid and the coefficient again becomes negative. Thus, for N2 gas below 621 K, a Joule–Thomson expansion can be used to cool the gas until liquid N2 forms.
Physical mechanism
There are two factors that can change the temperature of a fluid during an adiabatic expansion: a change in internal energy or the conversion between potential and kinetic internal energy.Temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
is the measure of thermal kinetic energy (energy associated with molecular motion); so a change in temperature indicates a change in thermal kinetic energy. The internal energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accoun ...
is the sum of thermal kinetic energy and thermal potential energy. Thus, even if the internal energy does not change, the temperature can change due to conversion between kinetic and potential energy; this is what happens in a free expansion and typically produces a decrease in temperature as the fluid expands.Pippard, A. B. (1957). "Elements of Classical Thermodynamics", p. 73. Cambridge University Press, Cambridge, U.K. If work is done on or by the fluid as it expands, then the total internal energy changes. This is what happens in a Joule–Thomson expansion and can produce larger heating or cooling than observed in a free expansion.
In a Joule–Thomson expansion the enthalpy remains constant. The enthalpy, , is defined as
:
where is internal energy, is pressure, and is volume. Under the conditions of a Joule–Thomson expansion, the change in represents the work done by the fluid (see the proof
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
below). If increases, with constant, then must decrease as a result of the fluid doing work on its surroundings. This produces a decrease in temperature and results in a positive Joule–Thomson coefficient. Conversely, a decrease in means that work is done on the fluid and the internal energy increases. If the increase in kinetic energy exceeds the increase in potential energy, there will be an increase in the temperature of the fluid and the Joule–Thomson coefficient will be negative.
For an ideal gas, does not change during a Joule–Thomson expansion. As a result, there is no change in internal energy; since there is also no change in thermal potential energy, there can be no change in thermal kinetic energy and, therefore, no change in temperature. In real gases, does change.
The ratio of the value of to that expected for an ideal gas at the same temperature is called the compressibility factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas ...
, . For a gas, this is typically less than unity at low temperature and greater than unity at high temperature (see the discussion in compressibility factor
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas ...
). At low pressure, the value of always moves towards unity as a gas expands.Atkins, Peter (1997). ''Physical Chemistry'' (6th ed.). New York: W.H. Freeman and Co. pp. 31–32. . Thus at low temperature, and will increase as the gas expands, resulting in a positive Joule–Thomson coefficient. At high temperature, and decrease as the gas expands; if the decrease is large enough, the Joule–Thomson coefficient will be negative.
For liquids, and for supercritical fluids under high pressure, increases as pressure increases. This is due to molecules being forced together, so that the volume can barely decrease due to higher pressure. Under such conditions, the Joule–Thomson coefficient is negative, as seen in the figure above.
The physical mechanism associated with the Joule–Thomson effect is closely related to that of a shock wave
In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a me ...
, although a shock wave differs in that the change in bulk kinetic energy of the gas flow is not negligible.
The Joule–Thomson (Kelvin) coefficient
Helium
Helium (from ) is a chemical element; it has chemical symbol, symbol He and atomic number 2. It is a colorless, odorless, non-toxic, inert gas, inert, monatomic gas and the first in the noble gas group in the periodic table. Its boiling point is ...
and hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
are two gases whose Joule–Thomson inversion temperatures at a pressure of one atmosphere
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
are very low (e.g., about 40 K, −233 °C for helium). Thus, helium and hydrogen warm when expanded at constant enthalpy at typical room temperatures. On the other hand, nitrogen
Nitrogen is a chemical element; it has Symbol (chemistry), symbol N and atomic number 7. Nitrogen is a Nonmetal (chemistry), nonmetal and the lightest member of pnictogen, group 15 of the periodic table, often called the Pnictogen, pnictogens. ...
and oxygen
Oxygen is a chemical element; it has chemical symbol, symbol O and atomic number 8. It is a member of the chalcogen group (periodic table), group in the periodic table, a highly reactivity (chemistry), reactive nonmetal (chemistry), non ...
, the two most abundant gases in air, have inversion temperatures of 621 K (348 °C) and 764 K (491 °C) respectively: these gases can be cooled from room temperature by the Joule–Thomson effect.
For an ideal gas, is always equal to zero: ideal gases neither warm nor cool upon being expanded at constant enthalpy.
Theoretical models
 For a Van der Waals gas, the coefficient iswith inversion temperature .
For the Dieterici gas, the reduced inversion temperature is , and the relation between reduced pressure and reduced inversion temperature is . This is plotted on the right. The critical point falls inside the region where the gas cools on expansion. The outside region is where the gas warms on expansion.
For a Van der Waals gas, the coefficient iswith inversion temperature .
For the Dieterici gas, the reduced inversion temperature is , and the relation between reduced pressure and reduced inversion temperature is . This is plotted on the right. The critical point falls inside the region where the gas cools on expansion. The outside region is where the gas warms on expansion.
Applications
In practice, the Joule–Thomson effect is achieved by allowing the gas to expand through a throttling device (usually avalve
A valve is a device or natural object that regulates, directs or controls the flow of a fluid (gases, liquids, fluidized solids, or Slurry, slurries) by opening, closing, or partially obstructing various passageways. Valves are technically Pip ...
) which must be very well insulated to prevent any heat transfer to or from the gas. No external work is extracted from the gas during the expansion (the gas must not be expanded through a turbine
A turbine ( or ) (from the Greek , ''tyrbē'', or Latin ''turbo'', meaning vortex) is a rotary mechanical device that extracts energy from a fluid flow and converts it into useful work. The work produced can be used for generating electrical ...
, for example).
The cooling produced in the Joule–Thomson expansion makes it a valuable tool in refrigeration
Refrigeration is any of various types of cooling of a space, substance, or system to lower and/or maintain its temperature below the ambient one (while the removed heat is ejected to a place of higher temperature).IIR International Dictionary of ...
. The effect is applied in the Linde technique as a standard process in the petrochemical industry
file:Jampilen Petrochemical Co. 02.jpg, 300px, Jampilen Petrochemical co., Asaluyeh, Iran
The petrochemical industry is concerned with the production and trade of petrochemicals. A major part is constituted by the plastics industry, plastics (poly ...
, where the cooling effect is used to liquefy gases, and in many cryogenic
In physics, cryogenics is the production and behaviour of materials at very low temperatures.
The 13th International Institute of Refrigeration's (IIR) International Congress of Refrigeration (held in Washington, DC in 1971) endorsed a univers ...
applications (e.g. for the production of liquid oxygen, nitrogen, and argon
Argon is a chemical element; it has symbol Ar and atomic number 18. It is in group 18 of the periodic table and is a noble gas. Argon is the third most abundant gas in Earth's atmosphere, at 0.934% (9340 ppmv). It is more than twice as abu ...
). A gas must be below its inversion temperature to be liquefied by the Linde cycle. For this reason, simple Linde cycle liquefiers, starting from ambient temperature, cannot be used to liquefy helium, hydrogen, or neon
Neon is a chemical element; it has symbol Ne and atomic number 10. It is the second noble gas in the periodic table. Neon is a colorless, odorless, inert monatomic gas under standard conditions, with approximately two-thirds the density of ...
. They must first be cooled to their inversion temperatures, which are −233 °C (helium), −71 °C (hydrogen), and −42 °C (neon).
Proof that the specific enthalpy remains constant
In thermodynamics so-called "specific" quantities are quantities per unit mass (kg) and are denoted by lower-case characters. So ''h'', ''u'', and ''v'' are the specific enthalpy, specific internal energy, and specific volume (volume per unit mass, or reciprocal density), respectively. In a Joule–Thomson process the specificenthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant extern ...
''h'' remains constant. To prove this, the first step is to compute the net work done when a mass ''m'' of the gas moves through the plug. This amount of gas has a volume of ''V''1 = ''m'' ''v''1 in the region at pressure ''P''1 (region 1) and a volume ''V''2 = ''m'' ''v''2 when in the region at pressure ''P''2 (region 2). Then in region 1, the "flow work" done ''on'' the amount of gas by the rest of the gas is: W1 = ''m'' ''P''1''v''1. In region 2, the work done ''by'' the amount of gas on the rest of the gas is: W2 = ''m'' ''P''2''v''2. So, the total work done ''on'' the mass ''m'' of gas is
:
The change in internal energy minus the total work done ''on'' the amount of gas is, by the first law of thermodynamics
The first law of thermodynamics is a formulation of the law of conservation of energy in the context of thermodynamic processes. For a thermodynamic process affecting a thermodynamic system without transfer of matter, the law distinguishes two ...
, the total heat supplied to the amount of gas.
:
In the Joule–Thomson process, the gas is insulated, so no heat is absorbed. This means that
:
where ''u''1 and ''u''2 denote the specific internal energies of the gas in regions 1 and 2, respectively. Using the definition of the specific enthalpy ''h = u + Pv'', the above equation implies that
:
where h1 and ''h''2 denote the specific enthalpies of the amount of gas in regions 1 and 2, respectively.
Throttling in the ''T''-''s'' diagram
 A convenient way to get a quantitative understanding of the throttling process is by using diagrams such as ''h''-''T'' diagrams, ''h''-''P'' diagrams, and others. Commonly used are the so-called ''T''-''s'' diagrams. Figure 2 shows the ''T''-''s'' diagram of nitrogen as an example. Various points are indicated as follows:
As shown before, throttling keeps ''h'' constant. E.g. throttling from 200 bar and 300K (point a in fig. 2) follows the isenthalpic (line of constant specific enthalpy) of 430kJ/kg. At 1 bar it results in point b which has a temperature of 270K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2K. Since the enthalpy is an extensive parameter the enthalpy in d (''h''d) is equal to the enthalpy in e (''h''e) multiplied with the mass fraction of the liquid in d (''x''d) plus the enthalpy in f (''h''f) multiplied with the mass fraction of the gas in d (1 − ''x''d). So
:
With numbers: 150 = ''x''d 28 + (1 − ''x''d) 230 so ''x''d is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.
A convenient way to get a quantitative understanding of the throttling process is by using diagrams such as ''h''-''T'' diagrams, ''h''-''P'' diagrams, and others. Commonly used are the so-called ''T''-''s'' diagrams. Figure 2 shows the ''T''-''s'' diagram of nitrogen as an example. Various points are indicated as follows:
As shown before, throttling keeps ''h'' constant. E.g. throttling from 200 bar and 300K (point a in fig. 2) follows the isenthalpic (line of constant specific enthalpy) of 430kJ/kg. At 1 bar it results in point b which has a temperature of 270K. So throttling from 200 bar to 1 bar gives a cooling from room temperature to below the freezing point of water. Throttling from 200 bar and an initial temperature of 133K (point c in fig. 2) to 1 bar results in point d, which is in the two-phase region of nitrogen at a temperature of 77.2K. Since the enthalpy is an extensive parameter the enthalpy in d (''h''d) is equal to the enthalpy in e (''h''e) multiplied with the mass fraction of the liquid in d (''x''d) plus the enthalpy in f (''h''f) multiplied with the mass fraction of the gas in d (1 − ''x''d). So
:
With numbers: 150 = ''x''d 28 + (1 − ''x''d) 230 so ''x''d is about 0.40. This means that the mass fraction of the liquid in the liquid–gas mixture leaving the throttling valve is 40%.
Derivation of the Joule–Thomson coefficient
It is difficult to think physically about what the Joule–Thomson coefficient, , represents. Also, modern determinations of do not use the original method used by Joule and Thomson, but instead measure a different, closely related quantity. Thus, it is useful to derive relationships between and other, more conveniently measured quantities, as described below. The first step in obtaining these results is to note that the Joule–Thomson coefficient involves the three variables ''T'', ''P'', and ''H''. A useful result is immediately obtained by applying the cyclic rule; in terms of these three variables that rule may be written : Each of the three partial derivatives in this expression has a specific meaning. The first is , the second is the constant pressureheat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
, , defined by
:
and the third is the inverse of the ''isothermal Joule–Thomson coefficient'', , defined by
:.
This last quantity is more easily measured than . Thus, the expression from the cyclic rule becomes
:
This equation can be used to obtain Joule–Thomson coefficients from the more easily measured isothermal Joule–Thomson coefficient. It is used in the following to obtain a mathematical expression for the Joule–Thomson coefficient in terms of the volumetric properties of a fluid.
To proceed further, the starting point is the fundamental equation of thermodynamics in terms of enthalpy; this is
:
Now "dividing through" by d''P'', while holding temperature constant, yields
:
The partial derivative on the left is the isothermal Joule–Thomson coefficient, , and the one on the right can be expressed in terms of the coefficient of thermal expansion via a Maxwell relation. The appropriate relation is
:
where ''α'' is the cubic coefficient of thermal expansion. Replacing these two partial derivatives yields
:
This expression can now replace in the earlier equation for to obtain:
:
This provides an expression for the Joule–Thomson coefficient in terms of the commonly available properties heat capacity, molar volume, and thermal expansion coefficient. It shows that the Joule–Thomson inversion temperature, at which is zero, occurs when the coefficient of thermal expansion is equal to the inverse of the temperature. Since this is true at all temperatures for ideal gases (see expansion in gases), the Joule–Thomson coefficient of an ideal gas is zero at all temperatures.
Joule's second law
It is easy to verify that for anideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
defined by suitable microscopic postulates that ''αT'' = 1, so the temperature change of such an ideal gas at a Joule–Thomson expansion is zero.
For such an ideal gas, this theoretical result implies that:
:''The internal energy of a fixed mass of an ideal gas depends only on its temperature (not pressure or volume).''
This rule was originally found by Joule experimentally for real gases and is known as Joule's second law. More refined experiments found important deviations from it.Bailyn, M. (1994). ''A Survey of Thermodynamics'', American Institute of Physics Press, New York, , p. 81.
See also
*Critical point (thermodynamics)
In thermodynamics, a critical point (or critical state) is the end point of a phase Equilibrium (thermodynamics), equilibrium curve. One example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designat ...
*Enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant extern ...
and Isenthalpic process
An isenthalpic process or isoenthalpic process is a process that proceeds without any change in enthalpy, ''H''; or specific enthalpy, ''h''.
Overview
If a steady-state, steady-flow process is analysed using a control volume, everything outside ...
*Ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
* Liquefaction of gases
* MIRI (Mid-Infrared Instrument), a J–T loop is used on one of the instruments of the James Webb Space Telescope
The James Webb Space Telescope (JWST) is a space telescope designed to conduct infrared astronomy. As the largest telescope in space, it is equipped with high-resolution and high-sensitivity instruments, allowing it to view objects too old, Lis ...
*Refrigeration
Refrigeration is any of various types of cooling of a space, substance, or system to lower and/or maintain its temperature below the ambient one (while the removed heat is ejected to a place of higher temperature).IIR International Dictionary of ...
*Reversible process (thermodynamics)
In thermodynamics, a reversible process is a process, involving a system and its surroundings, whose direction can be reversed by infinitesimal changes in some properties of the surroundings, such as pressure or temperature.
Throughout an enti ...
References
Bibliography
* * *External links
* * *Joule–Thomson effect module
University of Notre Dame {{DEFAULTSORT:Joule-Thomson effect Thermodynamics Cryogenics Engineering thermodynamics Gases Heating, ventilation, and air conditioning Thomson effect William Thomson, 1st Baron Kelvin