Image rectification on:
[Wikipedia]
[Google]
[Amazon]
Image rectification is a transformation process used to project images onto a common image plane. This process has several degrees of freedom and there are many strategies for transforming images to the common plane. Image rectification is used in computer stereo vision to simplify the problem of finding matching points between images (i.e. the 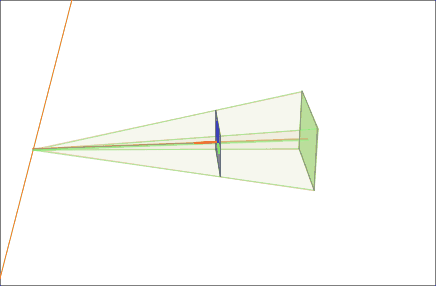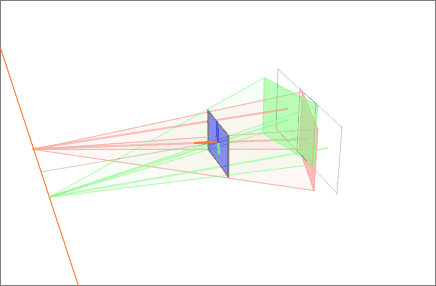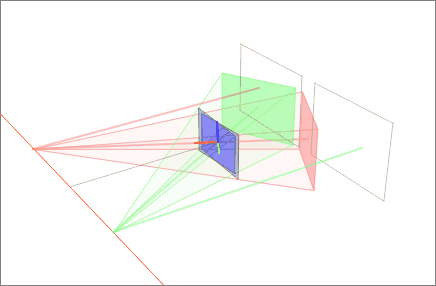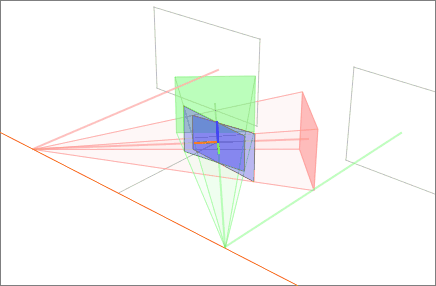
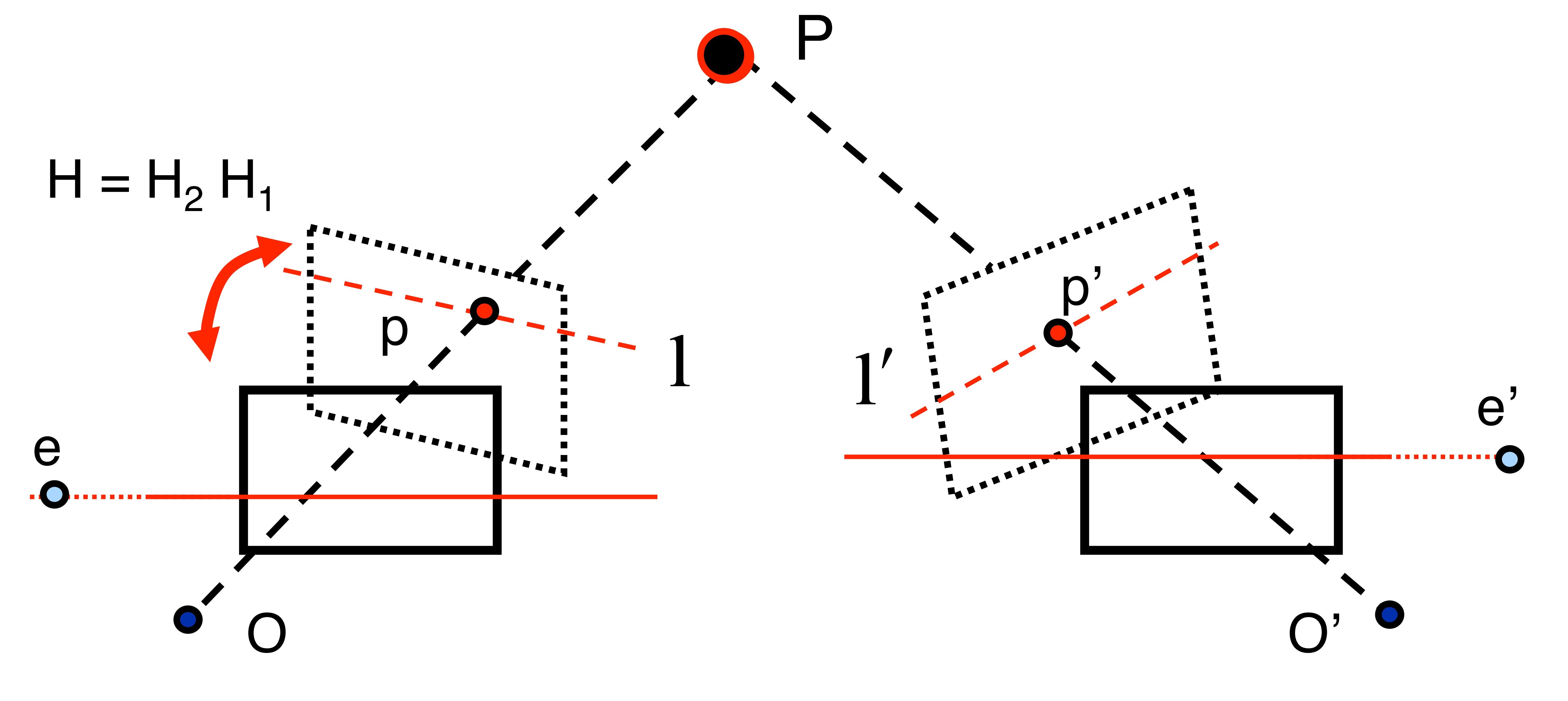
 Our model for this example is based on a pair of images that observe a 3D point ''P'', which corresponds to ''p'' and ''p' '' in the pixel coordinates of each image. ''O'' and ''O' '' represent the optical centers of each camera, with known camera matrices
Our model for this example is based on a pair of images that observe a 3D point ''P'', which corresponds to ''p'' and ''p' '' in the pixel coordinates of each image. ''O'' and ''O' '' represent the optical centers of each camera, with known camera matrices
correspondence problem
The correspondence problem refers to the problem of ascertaining which parts of one image correspond to which parts of another image, where differences are due to movement of the camera, the elapse of time, and/or movement of objects in the photo ...
), and in geographic information system
A geographic information system (GIS) is a type of database containing geographic data (that is, descriptions of phenomena for which location is relevant), combined with software tools for managing, analyzing, and visualizing those data. In a ...
s to merge images taken from multiple perspectives into a common map coordinate system.

In computer vision
Computer stereo vision takes two or more images with known relative camera positions that show an object from different viewpoints. For each pixel it then determines the corresponding scene point's depth (i.e. distance from the camera) by first finding matching pixels (i.e. pixels showing the same scene point) in the other image(s) and then applyingtriangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points.
Applications
In surveying
Specifically in surveying, triangulation involves only angle ...
to the found matches to determine their depth.
Finding matches in stereo vision is restricted by epipolar geometry
Epipolar geometry is the geometry of stereo vision. When two cameras view a 3D scene from two distinct positions, there are a number of geometric relations between the 3D points and their projections onto the 2D images that lead to constraints ...
: Each pixel's match in another image can only be found on a line called the epipolar line.
If two images are coplanar, i.e. they were taken such that the right camera is only offset horizontally compared to the left camera (not being moved towards the object or rotated), then each pixel's epipolar line is horizontal and at the same vertical position as that pixel. However, in general settings (the camera does move towards the object or rotate) the epipolar lines are slanted. Image rectification warps both images such that they appear as if they have been taken with only a horizontal displacement and as a consequence all epipolar lines are horizontal, which slightly simplifies the stereo matching process. Note however, that rectification does not fundamentally change the stereo matching process: It searches on lines, slanted ones before and horizontal ones after rectification.
Image rectification is also an equivalent (and more often used) alternative to perfect camera coplanarity. Even with high-precision equipment, image rectification is usually performed because it may be impractical to maintain perfect coplanarity between cameras.
Image rectification can only be performed with two images at a time and simultaneous rectification of more than two images is generally impossible.
Transformation
If the images to be rectified are taken from camera pairs without geometricdistortion
In signal processing, distortion is the alteration of the original shape (or other characteristic) of a signal. In communications and electronics it means the alteration of the waveform of an information-bearing signal, such as an audio s ...
, this calculation can easily be made with a linear transformation
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that pr ...
. X & Y rotation puts the images on the same plane, scaling makes the image frames be the same size and Z rotation & skew adjustments make the image pixel rows directly line up. The rigid alignment of the cameras needs to be known (by calibration) and the calibration coefficients are used by the transform.
In performing the transform, if the cameras themselves are calibrated for internal parameters, an essential matrix provides the relationship between the cameras. The more general case (without camera calibration) is represented by the fundamental matrix. If the fundamental matrix is not known, it is necessary to find preliminary point correspondences between stereo images to facilitate its extraction.
Algorithms
There are three main categories for image rectification algorithms: planar rectification, cylindrical rectification and polar rectification.Implementation details
All rectified images satisfy the following two properties: * All epipolar lines are parallel to the horizontal axis. * Corresponding points have identical vertical coordinates. In order to transform the original image pair into a rectified image pair, it is necessary to find aprojective transformation
In projective geometry, a homography is an isomorphism of projective spaces, induced by an isomorphism of the vector spaces from which the projective spaces derive. It is a bijection that maps lines to lines, and thus a collineation. In genera ...
''H''. Constraints are placed on ''H'' to satisfy the two properties above. For example, constraining the epipolar lines to be parallel with the horizontal axis means that epipoles must be mapped to the infinite point '' ,0,0sup>T'' in homogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. ...
. Even with these constraints, ''H'' still has four degrees of freedom. It is also necessary to find a matching ''H' '' to rectify the second image of an image pair. Poor choices of ''H'' and ''H' '' can result in rectified images that are dramatically changed in scale or severely distorted.
There are many different strategies for choosing a projective transform ''H'' for each image from all possible solutions. One advanced method is minimizing the disparity or least-square difference of corresponding points on the horizontal axis of the rectified image pair. Another method is separating ''H'' into a specialized projective transform, similarity transform, and shearing transform to minimize image distortion. One simple method is to rotate both images to look perpendicular to the line joining their collective optical centers, twist the optical axes so the horizontal axis of each image points in the direction of the other image's optical center, and finally scale the smaller image to match for line-to-line correspondence. This process is demonstrated in the following example.
Example

 Our model for this example is based on a pair of images that observe a 3D point ''P'', which corresponds to ''p'' and ''p' '' in the pixel coordinates of each image. ''O'' and ''O' '' represent the optical centers of each camera, with known camera matrices
Our model for this example is based on a pair of images that observe a 3D point ''P'', which corresponds to ''p'' and ''p' '' in the pixel coordinates of each image. ''O'' and ''O' '' represent the optical centers of each camera, with known camera matrices