Hénon map

In mathematics, the Hénon map, sometimes called Hénon–Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point in the plane and maps it to a new point

:$\beginx_ = 1 - a x_n^2 + y_n\\y_ = b x_n.\end$

The map depends on two parameters, and , which for the classical Hénon map have values of and . For the classical values the Hénon map is chaotic. For other values of and the map may be chaotic, intermittent, or converge to a periodic orbit. An overview of the type of behavior of the map at different parameter values may be obtained from its orbit diagram.

The map was introduced by Michel Hénon as a simplified model of the Poincaré section of the Lorenz model. For the classical map, an initial point of the plane will either approach a set of points known as the Hénon strange attractor, or diverge to infinity. The Hénon attractor is a fractal, smooth in one direction and a Cantor set in another. Numerical estimates yield a correlation dimension of 1.21 ± 0.01 or 1.25 ± 0.02 (depending on the dimension of the embedding space) and a Box Counting dimension of 1.261 ± 0.003 for the attractor of the classical map.

Attractor

The Hénon map maps two points into themselves: these are the invariant points. For the classical values of ''a'' and ''b'' of the Hénon map, one of these points is on the attractor:

: $x = \frac \approx 0.631354477,$
: $y = \frac \approx 0.189406343.$

This point is unstable. Points close to this fixed point and along the slope 1.924 will approach the fixed point and points along the slope -0.156 will move away from the fixed point. These slopes arise from the linearizations of the stable manifold and unstable manifold of the fixed point. The unstable manifold of the fixed point in the attractor is contained in the strange attractor of the Hénon map.

The Hénon map does not have a strange attractor for all values of the parameters ''a'' and ''b''. For example, by keeping ''b'' fixed at 0.3 the bifurcation diagram shows that for ''a'' = 1.25 the Hénon map has a stable periodic orbit as an attractor.

Cvitanović et al. have shown how the structure of the Hénon strange attractor can be understood in terms of unstable periodic orbits within the attractor.

Relationship to bifurcation diagram

If multiple Hénon maps are plotted, for each map varying the value of ''b'', then stacking all maps together, a Bifurcation diagram is produced. A Bifurcation diagram that is folded like a taco. Hence its boomerang shape when viewed in 2D from the top.

Decomposition

The Hénon map may be decomposed into the composition of three functions acting on the domain one after the other.

1) an area-preserving bend:
: $(x_1, y_1) = (x, 1 - ax^2 + y)\,$,

2) a contraction in the ''x'' direction:
: $(x_2, y_2) = (bx_1, y_1)\,$,

3) a reflection in the line ''y'' = ''x'':
: $(x_3, y_3) = (y_2, x_2)\,$.

One-dimensional decomposition

The Hénon map may also be deconstructed into a one-dimensional map, defined similarly to the Fibonacci Sequence.
:$x_ = 1-a x_n^2 + b x_$

Four-dimensional extension

Although the Hénon map can be plotted on the ''x''- and ''y''-axes, by varying ''a'' and ''b'', we obtain two additional dimensions for plotting. The Hénon map therefore, can be plotted in four-dimensional space. We can visualize such a plot by viewing one hyperplane (i.e. one cube of space) at a time representing three axes, then moving along the fourth axis as time passes.

In the video example to the right, the three axes for each image in the video are ''x'', ''y'', and ''b''. As time passes, it is the ''a'' axis that is moved through.

Special cases and low-period orbits

If one solves the one-dimensional Hénon map for the special case:
: $X = x_ = x_n = x_$
One arrives at the simple quadradic:
: $X = 1-a X^2 + b X$
Or
: $0 = -a X^2 + (b-1) X + 1$

The quadratic formula yields:
: $X =$

In the special case b=1, this is simplified to
: $X =$

If, in addition, a is in the form $$ the formula is further simplified to
: $X = \pm c^$

In practice the starting point (X,X) will follow a 4-point loop in two dimensions passing through all quadrants.

: $(X,X) = (X,-X)$
: $(X,-X) = (-X,-X)$
: $(-X,-X) = (-X,X)$
: $(-X,X) = (X,X)$

History

In 1976 France, the Lorenz attractor is analyzed by the physicist Yves Pomeau who performs a series of numerical calculations with J.L. Ibanez. The analysis produces a kind of complement to the work of Ruelle (and Lanford) presented in 1975. It is the Lorenz attractor, that is to say, the one corresponding to the original differential equations, and its geometric structure that interest them. Pomeau and Ibanez combine their numerical calculations with the results of mathematical analysis, based on the use of Poincaré sections. Stretching, folding, sensitivity to initial conditions are naturally brought in this context in connection with the Lorenz attractor. If the analysis is ultimately very mathematical, Pomeau and Ibanez follow, in a sense, a physicist approach, experimenting with the Lorenz system numerically.

Two openings are brought specifically by these experiences. They make it possible to highlight a singular behavior of the Lorenz system: there is a transition, characterized by a critical value of the parameters of the system, for which the system switches from a strange attractor position to a configuration in a limit cycle. The importance will be revealed by Pomeau himself (and a collaborator, Paul Manneville) through the "scenario" of Intermittency, proposed in 1979.

The second path suggested by Pomeau and Ibanez is the idea of realizing dynamical systems even simpler than that of Lorenz, but having similar characteristics, and which would make it possible to prove more clearly "evidences" brought to light by numerical calculations. Since the reasoning is based on Poincaré's section, he proposes to produce an application of the plane in itself, rather than a differential equation, imitating the behavior of Lorenz and its strange attractor. He builds one in an ad hoc manner which allows him to better base his reasoning.

In January 1976, Pomeau presented his work during a seminar given at the Côte d'Azur Observatory, attended by Michel Hénon. Michel Hénon uses Pomeau’s suggestion to obtain a simple system with a strange attractor.

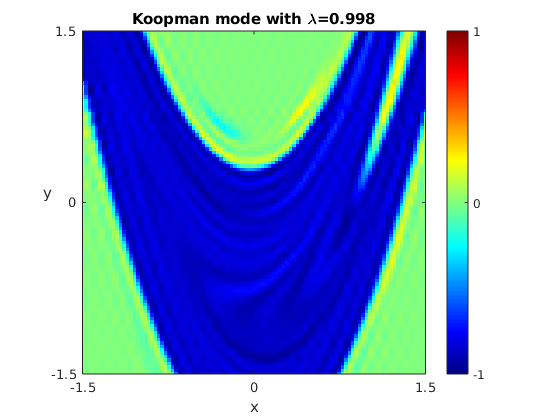
Koopman modes

In dynamical system, the Koopman operator is a natural linear operator on the space of scalar fields. For general nonlinear systems, the eigenfunctions of this operator cannot be expressed in any nice form. Instead one must compute them numerically. These modes can give insight into the symbolic dynamics of chaotic maps like the Hénon map. In the mode provided, the stable manifold of the strange attractor can be clearly seen.

Generalizations

A 3-D generalization for the Hénon map was proposed by Hitz and Zele. It is given by

$\mathbf(n+1)= \begin s_1(n+1) \\ s_2(n+1) \\ s_3(n+1) \end = \begin -\alpha s_1^2(n)+s_3(n)+1\\ -\beta s_1(n)\\ \beta s_1(n) + s_2(n) \end$.

For $\alpha=1.07$ and $\beta=0.3$ it can be shown that almost all initial conditions inside the unit sphere generate chaotic signals with largest Lyapunov exponent $0.23$.

Many other generalizations have been proposed in the literature. One can generate, for example, band-limited chaotic signals using digital filters in the feedback loop of the system.

See also

* Horseshoe map
* Takens' theorem

Notes

References

*
*
*
*
* . Reprinted in: Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 69–71, 1998
*

External links

Interactive Henon map
an

i



by A. Luhn

Orbit Diagram of the Hénon Map
by C. Pellicer-Lostao and R. Lopez-Ruiz after work by Ed Pegg Jr, The Wolfram Demonstrations Project.

Matlab code for the Hénon Map
by M.Suzen


of Hénon map in javascript (experiences.math.cnrs.fr) by Marc Monticelli.

{{DEFAULTSORT:Henon Map
Chaotic maps