gnomonic projection

A gnomonic projection, also known as a central projection or rectilinear projection, is a perspective projection of a sphere, with center of projection at the sphere's center, onto any plane not passing through the center, most commonly a tangent plane. Under gnomonic projection every great circle on the sphere is projected to a straight line in the plane (a great circle is a geodesic on the sphere, the shortest path between any two points, analogous to a straight line on the plane). More generally, a gnomonic projection can be taken of any -dimensional hypersphere onto a hyperplane.

The projection is the -dimensional generalization of the trigonometric tangent which maps from the circle to a straight line, and as with the tangent, every pair of antipodal points on the sphere projects to a single point in the plane, while the points on the plane through the sphere's center and parallel to the image plane project to points at infinity; often the projection is considered as a one-to-one correspondence between points in the hemisphere and points in the plane, in which case any finite part of the image plane represents a portion of the hemisphere.

The gnomonic projection is azimuthal (radially symmetric). No shape distortion occurs at the center of the projected image, but distortion increases rapidly away from it.

The gnomonic projection originated in astronomy for constructing sundials and charting the celestial sphere. It is commonly used as a geographic map projection, and can be convenient in navigation because great-circle courses are plotted as straight lines. Rectilinear photographic lenses make a perspective projection of the world onto an image plane; this can be thought of as a gnomonic projection of the image sphere (an abstract sphere indicating the direction of each ray passing through a camera modeled as a pinhole). The gnomonic projection is used in crystallography for analyzing the orientations of lines and planes of crystal structures. It is used in structural geology for analyzing the orientations of fault planes. In computer graphics and computer representation of spherical data, cube mapping is the gnomonic projection of the image sphere onto six faces of a cube.

In mathematics, the space of orientations of undirected lines in 3-dimensional space is called the real projective plane, and is typically pictured either by the "projective sphere" or by its gnomonic projection. When the angle between lines is imposed as a measure of distance, this space is called the elliptic plane. The gnomonic projection of the 3-sphere of unit quaternions, points of which represent 3-dimensional rotations, results in Rodrigues vectors. The gnomonic projection of the hyperboloid of two sheets, treated as a model for the hyperbolic plane, is called the Beltrami–Klein model.

History

The gnomonic projection is said to be the oldest map projection, speculatively attributed to Thales who may have used it for star maps in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map.

Properties

The gnomonic projection is from the centre of a sphere to a plane tangent to the sphere (Fig 1 below). The sphere and the plane touch at the tangent point. Great circles transform to straight lines via the gnomonic projection. Since meridians (lines of longitude) and the equator are great circles, they are always shown as straight lines on a gnomonic map. Since the projection is from the centre of the sphere, a gnomonic map can represent less than half of the area of the sphere. Distortion of the scale of the map increases from the centre (tangent point) to the periphery.

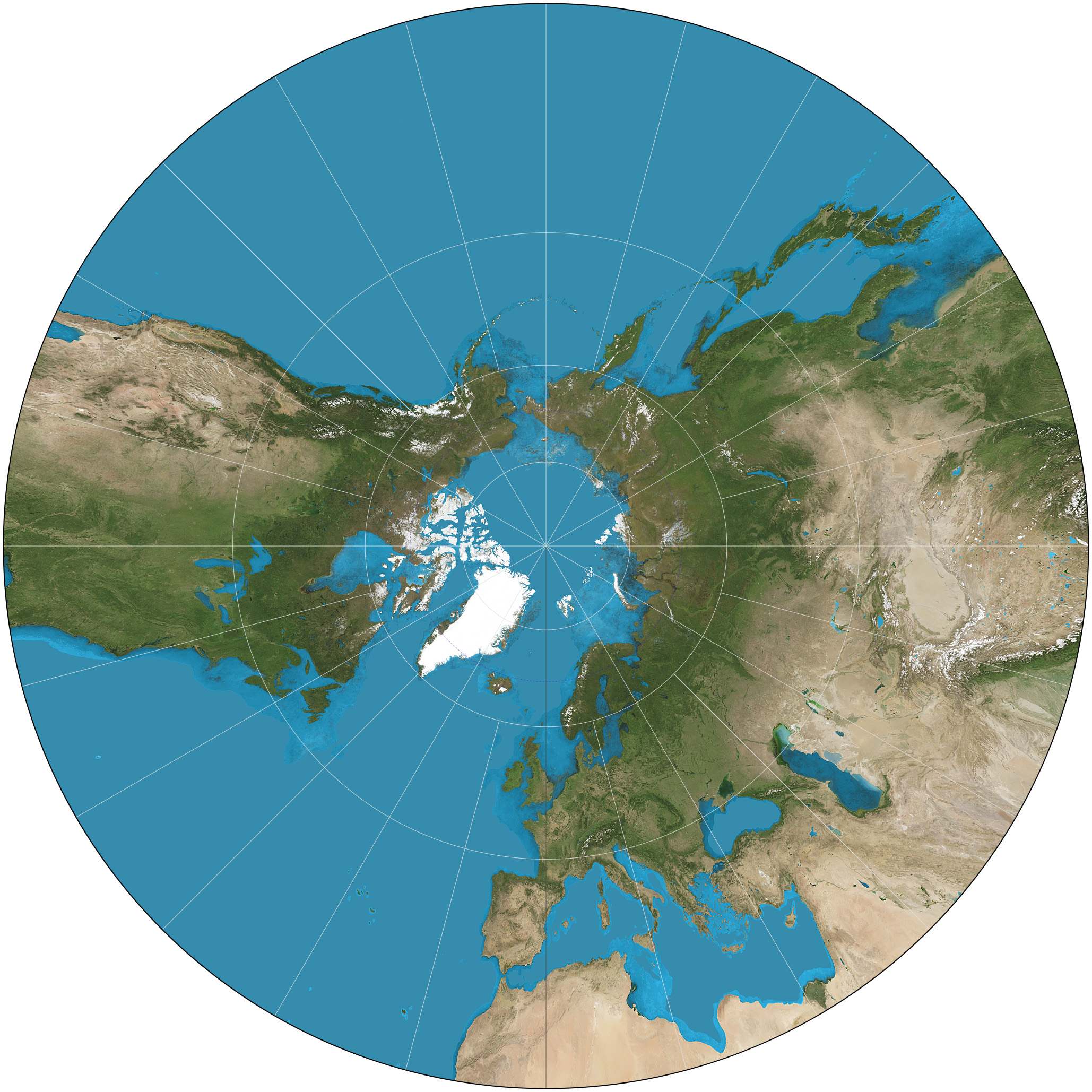
*If the tangent point is one of the poles then the meridians are radial and equally spaced (Fig 2 below). The equator cannot be shown as it is at infinity in all directions. Other parallels (lines of latitude) are depicted as concentric circles.

*If the tangent point is on the equator then the meridians are parallel but not equally spaced (Fig 3 below). The equator is a straight line perpendicular to the meridians. Other parallels are depicted as hyperbolae.

*If the tangent point is not on a pole or the equator, then the meridians are radially outward straight lines from a pole, but not equally spaced (Fig 4 below). The equator is a straight line that is perpendicular to only one meridian, indicating that the projection is not conformal. Other parallels are depicted as conic sections.

As with all azimuthal projections, angles from the tangent point are preserved. The map distance from that point is a function ''r''(''d'') of the true distance ''d'', given by

:$r(d) = R\,\tan \frac d R$

where ''R'' is the radius of the Earth. The radial scale is

:$r'(d) = \frac$

and the transverse scale

: $\frac$

so the transverse scale increases outwardly, and the radial scale even more.

Use

Gnomonic projections are used in seismic work because seismic waves tend to travel along great circles. They are also used by navies in plotting direction finding bearings, since radio signals travel along great circles. Meteors also travel along great circles, with the Gnomonic Atlas Brno 2000.0 being the IMO's recommended set of star charts for visual meteor observations. Aircraft and ship navigators use the projection to find the shortest route between start and destination. The track is first drawn on the gnomonic chart, then transferred to a Mercator chart for navigation.

The gnomonic projection is used extensively in photography, where it is called '' rectilinear projection'', as it naturally arises from the pinhole camera model where the screen is a plane. Because they are equivalent, the same viewer used for photographic panoramas can be used to render gnomonic maps .

The gnomonic projection is used in astronomy where the tangent point is centered on the object of interest. The sphere being projected in this case is the celestial sphere, ''R'' = 1, and not the surface of the Earth.

In astronomy, gnomic projection star charts of the celestial sphere can be used by observers to accurately plot the straight line path of a meteor trail.

See also

* Local tangent plane
* List of map projections
* Beltrami–Klein model, the analogous mapping of the hyperbolic plane

References

Further reading

*
*
*
*
*
*
*
*
*
*
*
*

External links

Gnomonic Projection

{{Map projections

Map projections
Navigation
Projective geometry