Geometric notation on:
[Wikipedia]
[Google]
[Amazon]
Geometry (; ) is a branch of
 The earliest recorded beginnings of geometry can be traced to ancient
The earliest recorded beginnings of geometry can be traced to ancient  Indian mathematicians also made many important contributions in geometry. The ''
Indian mathematicians also made many important contributions in geometry. The ''

 A
A
 A
A

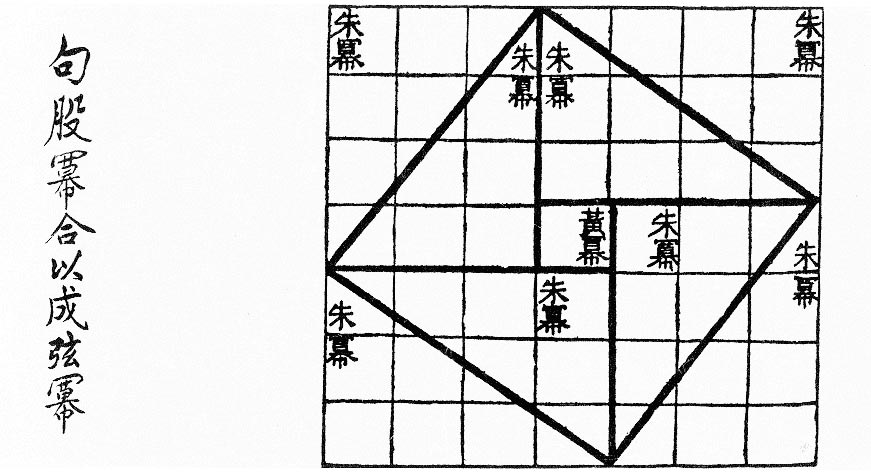 The concept of length or distance can be generalized, leading to the idea of
The concept of length or distance can be generalized, leading to the idea of
 Traditional geometry allowed dimensions 1 (a line or curve), 2 (a Plane (mathematics), plane or surface), and 3 (our ambient world conceived of as three-dimensional space). Furthermore, mathematicians and physicists have used higher dimensions for nearly two centuries. One example of a mathematical use for higher dimensions is the configuration space (physics), configuration space of a physical system, which has a dimension equal to the system's degrees of freedom. For instance, the configuration of a screw can be described by five coordinates.
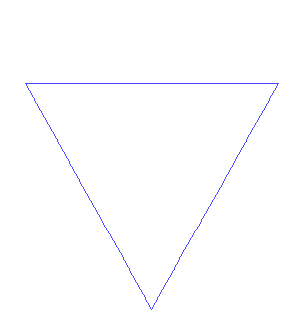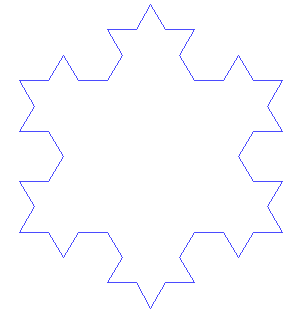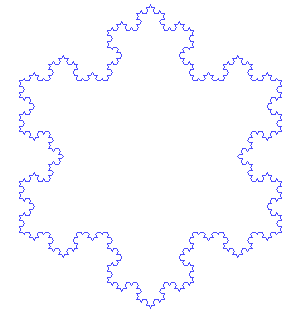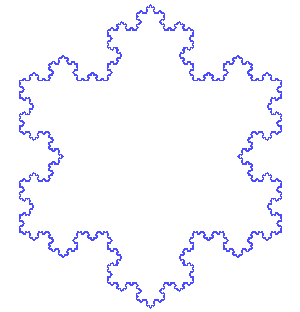
In general topology, the concept of dimension has been extended from natural numbers, to infinite dimension (Hilbert spaces, for example) and positive real numbers (in fractal geometry). In
Traditional geometry allowed dimensions 1 (a line or curve), 2 (a Plane (mathematics), plane or surface), and 3 (our ambient world conceived of as three-dimensional space). Furthermore, mathematicians and physicists have used higher dimensions for nearly two centuries. One example of a mathematical use for higher dimensions is the configuration space (physics), configuration space of a physical system, which has a dimension equal to the system's degrees of freedom. For instance, the configuration of a screw can be described by five coordinates.
In general topology, the concept of dimension has been extended from natural numbers, to infinite dimension (Hilbert spaces, for example) and positive real numbers (in fractal geometry). In
 The theme of
The theme of
 Differential geometry uses techniques of
Differential geometry uses techniques of
 Topology is the field concerned with the properties of continuous mappings, and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as connectedness and compact (topology), compactness.
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are
Topology is the field concerned with the properties of continuous mappings, and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as connectedness and compact (topology), compactness.
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are
 Algebraic geometry is fundamentally the study by means of algebraic methods of some geometrical shapes, called algebraic sets, and defined as common zero of a function, zeros of multivariate polynomials. Algebraic geometry became an autonomous subfield of geometry , with a theorem called Hilbert's Nullstellensatz that establishes a strong correspondence between algebraic sets and ideal (ring theory), ideals of polynomial rings. This led to a parallel development of algebraic geometry, and its algebraic counterpart, called commutative algebra. From the late 1950s through the mid-1970s algebraic geometry had undergone major foundational development, with the introduction by Alexander Grothendieck of scheme theory, which allows using algebraic topology, topological methods, including cohomology theory, cohomology theories in a purely algebraic context. Scheme theory allowed to solve many difficult problems not only in geometry, but also in number theory. Wiles' proof of Fermat's Last Theorem is a famous example of a long-standing problem of number theory whose solution uses scheme theory and its extensions such as stack (mathematics), stack theory. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.
Algebraic geometry has applications in many areas, including cryptography and
Algebraic geometry is fundamentally the study by means of algebraic methods of some geometrical shapes, called algebraic sets, and defined as common zero of a function, zeros of multivariate polynomials. Algebraic geometry became an autonomous subfield of geometry , with a theorem called Hilbert's Nullstellensatz that establishes a strong correspondence between algebraic sets and ideal (ring theory), ideals of polynomial rings. This led to a parallel development of algebraic geometry, and its algebraic counterpart, called commutative algebra. From the late 1950s through the mid-1970s algebraic geometry had undergone major foundational development, with the introduction by Alexander Grothendieck of scheme theory, which allows using algebraic topology, topological methods, including cohomology theory, cohomology theories in a purely algebraic context. Scheme theory allowed to solve many difficult problems not only in geometry, but also in number theory. Wiles' proof of Fermat's Last Theorem is a famous example of a long-standing problem of number theory whose solution uses scheme theory and its extensions such as stack (mathematics), stack theory. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.
Algebraic geometry has applications in many areas, including cryptography and
 Discrete geometry is a subject that has close connections with convex geometry. It is concerned mainly with questions of relative position of simple geometric objects, such as points, lines and circles. Examples include the study of sphere packings, triangulation (geometry), triangulations, the Kneser-Poulsen conjecture, etc. It shares many methods and principles with combinatorics.
Discrete geometry is a subject that has close connections with convex geometry. It is concerned mainly with questions of relative position of simple geometric objects, such as points, lines and circles. Examples include the study of sphere packings, triangulation (geometry), triangulations, the Kneser-Poulsen conjecture, etc. It shares many methods and principles with combinatorics.
 Mathematics and art are related in a variety of ways. For instance, the theory of perspective (graphical), perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of
Mathematics and art are related in a variety of ways. For instance, the theory of perspective (graphical), perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of
 Calculus was strongly influenced by geometry. For instance, the introduction of coordinates by
Calculus was strongly influenced by geometry. For instance, the introduction of coordinates by
''Unusual Geometry Problems''
''The Math Forum'' – Geometry
*
*
*
Nature Precedings – ''Pegs and Ropes Geometry at Stonehenge''
* [https://web.archive.org/web/20071004174210/http://www.gresham.ac.uk/event.asp?PageId=45&EventId=618 "4000 Years of Geometry"], lecture by Robin Wilson given at Gresham College, 3 October 2007 (available for MP3 and MP4 download as well as a text file) *
Finitism in Geometry
at the Stanford Encyclopedia of Philosophy
Interactive geometry reference with hundreds of applets
Geometry classes
at Khan Academy {{Authority control Geometry,
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, which includes the notions of point, line, plane, distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
, angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
, surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
, and curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
, as fundamental concepts.
Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and construction, constructi ...
, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive number, positive integers , , and satisfy the equation for any integer value of greater than . The cases ...
, a problem that was stated in terms of elementary arithmetic
Elementary arithmetic is a branch of mathematics involving addition, subtraction, multiplication, and Division (mathematics), division. Due to its low level of abstraction, broad range of application, and position as the foundation of all mathema ...
, and remained unsolved for several centuries.
During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
's ("remarkable theorem") that asserts roughly that the Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
of a surface is independent from any specific embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup.
When some object X is said to be embedded in another object Y ...
in a Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
s and Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as manifold, smooth manifolds with a ''Riemannian metric'' (an inner product on the tangent space at each point that varies smooth function, smo ...
. Later in the 19th century, it appeared that geometries without the parallel postulate
In geometry, the parallel postulate is the fifth postulate in Euclid's ''Elements'' and a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior ...
(non-Euclidean geometries
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
) can be developed without introducing any contradiction. The geometry that underlies general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
is a famous application of non-Euclidean geometry.
Since the late 19th century, the scope of geometry has been greatly expanded, and the field has been split in many subfields that depend on the underlying methods—differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
, algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, computational geometry, algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
, discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geom ...
(also known as ''combinatorial geometry''), etc.—or on the properties of Euclidean spaces that are disregarded—projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
that consider only alignment of points but not distance and parallelism, affine geometry
In mathematics, affine geometry is what remains of Euclidean geometry when ignoring (mathematicians often say "forgetting") the metric notions of distance and angle.
As the notion of '' parallel lines'' is one of the main properties that is i ...
that omits the concept of angle and distance, finite geometry
A finite geometry is any geometry, geometric system that has only a finite set, finite number of point (geometry), points.
The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based ...
that omits continuity, and others. This enlargement of the scope of geometry led to a change of meaning of the word "space", which originally referred to the three-dimensional space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
of the physical world and its model
A model is an informative representation of an object, person, or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin , .
Models can be divided in ...
provided by Euclidean geometry; presently a geometric space, or simply a ''space'' is a mathematical structure
In mathematics, a structure on a set (or on some sets) refers to providing or endowing it (or them) with certain additional features (e.g. an operation, relation, metric, or topology). Τhe additional features are attached or related to the ...
on which some geometry is defined.
History
 The earliest recorded beginnings of geometry can be traced to ancient
The earliest recorded beginnings of geometry can be traced to ancient Mesopotamia
Mesopotamia is a historical region of West Asia situated within the Tigris–Euphrates river system, in the northern part of the Fertile Crescent. Today, Mesopotamia is known as present-day Iraq and forms the eastern geographic boundary of ...
and Egypt
Egypt ( , ), officially the Arab Republic of Egypt, is a country spanning the Northeast Africa, northeast corner of Africa and Western Asia, southwest corner of Asia via the Sinai Peninsula. It is bordered by the Mediterranean Sea to northe ...
in the 2nd millennium BC. Early geometry was a collection of empirically discovered principles concerning lengths, angles, areas, and volumes, which were developed to meet some practical need in surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
, construction
Construction are processes involved in delivering buildings, infrastructure, industrial facilities, and associated activities through to the end of their life. It typically starts with planning, financing, and design that continues until the a ...
, astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, and various crafts. The earliest known texts on geometry are the Egyptian
''Egyptian'' describes something of, from, or related to Egypt.
Egyptian or Egyptians may refer to:
Nations and ethnic groups
* Egyptians, a national group in North Africa
** Egyptian culture, a complex and stable culture with thousands of year ...
Rhind Papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057, pBM 10058, and Brooklyn Museum 37.1784Ea-b) is one of the best known examples of ancient Egyptian mathematics.
It is one of two well-known mathematical papyr ...
(2000–1800 BC) and Moscow Papyrus (), and the Babylonian clay tablets, such as Plimpton 322
Plimpton 322 is a Babylonian clay tablet, believed to have been written around 1800 BC, that contains a mathematical table written in cuneiform script. Each row of the table relates to a Pythagorean triple, that is, a triple of integers (s ...
(1900 BC). For example, the Moscow Papyrus gives a formula for calculating the volume of a truncated pyramid, or frustum
In geometry, a ; (: frusta or frustums) is the portion of a polyhedron, solid (normally a pyramid (geometry), pyramid or a cone (geometry), cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces a ...
. Later clay tablets (350–50 BC) demonstrate that Babylonian astronomers implemented trapezoid
In geometry, a trapezoid () in North American English, or trapezium () in British English, is a quadrilateral that has at least one pair of parallel sides.
The parallel sides are called the ''bases'' of the trapezoid. The other two sides are ...
procedures for computing Jupiter's position and motion
In physics, motion is when an object changes its position with respect to a reference point in a given time. Motion is mathematically described in terms of displacement, distance, velocity, acceleration, speed, and frame of reference to an o ...
within time-velocity space. These geometric procedures anticipated the Oxford Calculators
The Oxford Calculators were a group of 14th-century thinkers, almost all associated with Merton College, Oxford; for this reason they were dubbed "The Merton School". Their work incorporated a logical and mathematical approach to philosophical p ...
, including the mean speed theorem, by 14 centuries. South of Egypt the ancient Nubians established a system of geometry including early versions of sun clocks.
In the 7th century BC, the Greek
Greek may refer to:
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group
*Greek language, a branch of the Indo-European language family
**Proto-Greek language, the assumed last common ancestor of all kno ...
mathematician Thales of Miletus
Thales of Miletus ( ; ; ) was an Ancient Greek pre-Socratic philosopher from Miletus in Ionia, Asia Minor. Thales was one of the Seven Sages, founding figures of Ancient Greece.
Beginning in eighteenth-century historiography, many came to ...
used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem
In geometry, Thales's theorem states that if , , and are distinct points on a circle where the line is a diameter, the angle is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as pa ...
. Pythagoras
Pythagoras of Samos (; BC) was an ancient Ionian Greek philosopher, polymath, and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of P ...
established the Pythagorean School
Pythagorean, meaning of or pertaining to the ancient Ionian mathematician, philosopher, and music theorist Pythagoras, may refer to:
Philosophy
* Pythagoreanism, the esoteric and metaphysical beliefs purported to have been held by Pythagoras
* N ...
, which is credited with the first proof of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, though the statement of the theorem has a long history. Eudoxus (408–) developed the method of exhaustion
The method of exhaustion () is a method of finding the area of a shape by inscribing inside it a sequence of polygons (one at a time) whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the differ ...
, which allowed the calculation of areas and volumes of curvilinear figures, as well as a theory of ratios that avoided the problem of incommensurable magnitudes, which enabled subsequent geometers to make significant advances. Around 300 BC, geometry was revolutionized by Euclid, whose '' Elements'', widely considered the most successful and influential textbook of all time, introduced mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as mat ...
through the axiomatic method
In mathematics and logic, an axiomatic system is a set of formal statements (i.e. axioms) used to logically derive other statements such as lemmas or theorems. A proof within an axiom system is a sequence of deductive steps that establis ...
and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the ''Elements'' were already known, Euclid arranged them into a single, coherent logical framework. The ''Elements'' was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today. Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
() of Syracuse, Italy
Syracuse ( ; ; ) is a historic city on the Italy, Italian island of Sicily, the capital of the Italian province of Syracuse. The city is notable for its rich Greek and Roman history, Greek culture, culture, amphitheatres, architecture, an ...
used the method of exhaustion to calculate the area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
under the arc of a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
with the summation of an infinite series, and gave remarkably accurate approximations of pi. He also studied the spiral
In mathematics, a spiral is a curve which emanates from a point, moving further away as it revolves around the point. It is a subtype of whorled patterns, a broad group that also includes concentric objects.
Two-dimensional
A two-dimension ...
bearing his name and obtained formulas for the volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
s of surfaces of revolution.
 Indian mathematicians also made many important contributions in geometry. The ''
Indian mathematicians also made many important contributions in geometry. The ''Shatapatha Brahmana
The Shatapatha Brahmana (, , abbreviated to 'SB') is a commentary on the Yajurveda, Śukla Yajurveda. It is attributed to the Vedic sage Yajnavalkya. Described as the most complete, systematic, and important of the Brahmanas (commentaries on the ...
'' (3rd century BC) contains rules for ritual geometric constructions that are similar to the ''Sulba Sutras
The ''Shulva Sutras'' or ''Śulbasūtras'' (Sanskrit: शुल्बसूत्र; ': "string, cord, rope") are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.
Purpose and origins
Th ...
''.
According to , the ''Śulba Sūtras'' contain "the earliest extant verbal expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians. They contain lists of Pythagorean triples, which are particular cases of Diophantine equations ''Diophantine'' means pertaining to the ancient Greek mathematician Diophantus. A number of concepts bear this name:
*Diophantine approximation
In number theory, the study of Diophantine approximation deals with the approximation of real n ...
.: "The arithmetic content of the ''Śulva Sūtras'' consists of rules for finding Pythagorean triples such as (3, 4, 5), (5, 12, 13), (8, 15, 17), and (12, 35, 37). It is not certain what practical use these arithmetic rules had. The best conjecture is that they were part of religious ritual. A Hindu home was required to have three fires burning at three different altars. The three altars were to be of different shapes, but all three were to have the same area. These conditions led to certain "Diophantine" problems, a particular case of which is the generation of Pythagorean triples, so as to make one square integer equal to the sum of two others."
In the Bakhshali manuscript, there are a handful of geometric problems (including problems about volumes of irregular solids). The Bakhshali manuscript also "employs a decimal place value system with a dot for zero." Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was the first of the major mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy. His works include the '' Āryabhaṭīya'' (which mentions that in 3600 ' ...
's ''Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Indian astronomy, Sanskrit astronomical treatise, is the ''Masterpiece, magnum opus'' and only known surviving work of the 5th century Indian mathematics, Indian mathematician Aryabhata. Philos ...
'' (499) includes the computation of areas and volumes.
Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
wrote his astronomical work '' '' in 628. Chapter 12, containing 66 Sanskrit
Sanskrit (; stem form ; nominal singular , ,) is a classical language belonging to the Indo-Aryan languages, Indo-Aryan branch of the Indo-European languages. It arose in northwest South Asia after its predecessor languages had Trans-cultural ...
verses, was divided into two sections: "basic operations" (including cube roots, fractions, ratio and proportion, and barter) and "practical mathematics" (including mixture, mathematical series, plane figures, stacking bricks, sawing of timber, and piling of grain). In the latter section, he stated his famous theorem on the diagonals of a cyclic quadrilateral
In geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral (four-sided polygon) whose vertex (geometry), vertices all lie on a single circle, making the sides Chord (geometry), chords of the circle. This circle is called ...
. Chapter 12 also included a formula for the area of a cyclic quadrilateral (a generalization of Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths Letting be the semiperimeter of the triangle, s = \tfrac12(a + b + c), the area is
A = \sqrt.
It is named after first-century ...
), as well as a complete description of rational triangle
An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational numbers; any rational triangle can be rescaled by the lowest common denominator of the s ...
s (''i.e.'' triangles with rational sides and rational areas).
In the Middle Ages
In the history of Europe, the Middle Ages or medieval period lasted approximately from the 5th to the late 15th centuries, similarly to the post-classical period of global history. It began with the fall of the Western Roman Empire and ...
, mathematics in medieval Islam
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built upon syntheses of Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important developments o ...
contributed to the development of geometry, especially algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
. Al-Mahani (b. 853) conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. Thābit ibn Qurra
Thābit ibn Qurra (full name: , , ; 826 or 836 – February 19, 901), was a scholar known for his work in mathematics, medicine, astronomy, and translation. He lived in Baghdad in the second half of the ninth century during the time of the Abba ...
(known as Thebit in Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
) (836–901) dealt with arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
operations applied to ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s of geometrical quantities, and contributed to the development of analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
. Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīshābūrī (18 May 1048 – 4 December 1131) (Persian language, Persian: غیاث الدین ابوالفتح عمر بن ابراهیم خیام نیشابورﻯ), commonly known as Omar ...
(1048–1131) found geometric solutions to cubic equation
In algebra, a cubic equation in one variable is an equation of the form
ax^3+bx^2+cx+d=0
in which is not zero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of th ...
s. The theorems of Ibn al-Haytham
Ḥasan Ibn al-Haytham (Latinization of names, Latinized as Alhazen; ; full name ; ) was a medieval Mathematics in medieval Islam, mathematician, Astronomy in the medieval Islamic world, astronomer, and Physics in the medieval Islamic world, p ...
(Alhazen), Omar Khayyam and Nasir al-Din al-Tusi
Muḥammad ibn Muḥammad ibn al-Ḥasan al-Ṭūsī (1201 – 1274), also known as Naṣīr al-Dīn al-Ṭūsī (; ) or simply as (al-)Tusi, was a Persians, Persian polymath, architect, Early Islamic philosophy, philosopher, Islamic medicine, phy ...
on quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
s, including the Lambert quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest s ...
and Saccheri quadrilateral, were part of a line of research on the parallel postulate
In geometry, the parallel postulate is the fifth postulate in Euclid's ''Elements'' and a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior ...
continued by later European geometers, including Vitello (), Gersonides
Levi ben Gershon (1288 – 20 April 1344), better known by his Graecized name as Gersonides, or by his Latinized name Magister Leo Hebraeus, or in Hebrew by the abbreviation of first letters as ''RaLBaG'', was a medieval French Jewish philosoph ...
(1288–1344), Alfonso, John Wallis
John Wallis (; ; ) was an English clergyman and mathematician, who is given partial credit for the development of infinitesimal calculus.
Between 1643 and 1689 Wallis served as chief cryptographer for Parliament and, later, the royal court. ...
, and Giovanni Girolamo Saccheri
Giovanni Girolamo Saccheri (; 5 September 1667 – 25 October 1733) was an Italian Jesuit priest, scholastic philosopher, and mathematician. He is considered the forerunner of non-Euclidean geometry.
Biography
The son of a lawyer, Saccheri w ...
, that by the 19th century led to the discovery of hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
.
In the early 17th century, there were two important developments in geometry. The first was the creation of analytic geometry, or geometry with coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the Position (geometry), position of the Point (geometry), points or other geometric elements on a manifold such as ...
and equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
s, by René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
(1596–1650) and Pierre de Fermat
Pierre de Fermat (; ; 17 August 1601 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he is recognized for his d ...
(1601–1665). This was a necessary precursor to the development of calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
and a precise quantitative science of physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
. The second geometric development of this period was the systematic study of projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
by Girard Desargues
Girard Desargues (; 21 February 1591September 1661) was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are named i ...
(1591–1661). Projective geometry studies properties of shapes which are unchanged under projections and sections
Section, Sectioning, or Sectioned may refer to:
Arts, entertainment and media
* Section (music), a complete, but not independent, musical idea
* Section (typography), a subdivision, especially of a chapter, in books and documents
** Section sig ...
, especially as they relate to artistic perspective.
Two developments in geometry in the 19th century changed the way it had been studied previously. These were the discovery of non-Euclidean geometries
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
by Nikolai Ivanovich Lobachevsky, János Bolyai and Carl Friedrich Gauss and of the formulation of symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
as the central consideration in the Erlangen programme of Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
(which generalized the Euclidean and non-Euclidean geometries). Two of the master geometers of the time were Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
(1826–1866), working primarily with tools from mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
, and introducing the Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed vers ...
, and Henri Poincaré
Jules Henri Poincaré (, ; ; 29 April 185417 July 1912) was a French mathematician, Theoretical physics, theoretical physicist, engineer, and philosophy of science, philosopher of science. He is often described as a polymath, and in mathemati ...
, the founder of algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
and the geometric theory of dynamical system
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
s. As a consequence of these major changes in the conception of geometry, the concept of "space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
" became something rich and varied, and the natural background for theories as different as complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
and classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
.
Main concepts
The following are some of the most important concepts in geometry.Axioms
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
took an abstract approach to geometry in his Elements, one of the most influential books ever written. Euclid introduced certain axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
s, or postulate
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
s, expressing primary or self-evident properties of points, lines, and planes. He proceeded to rigorously deduce other properties by mathematical reasoning. The characteristic feature of Euclid's approach to geometry was its rigor, and it has come to be known as ''axiomatic'' or ''synthetic
Synthetic may refer to:
Science
* Synthetic biology
* Synthetic chemical or compound, produced by the process of chemical synthesis
* Synthetic elements, chemical elements that are not naturally found on Earth and therefore have to be created in ...
'' geometry. At the start of the 19th century, the discovery of non-Euclidean geometries
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
by Nikolai Ivanovich Lobachevsky (1792–1856), János Bolyai (1802–1860), Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
(1777–1855) and others led to a revival of interest in this discipline, and in the 20th century, David Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician and philosopher of mathematics and one of the most influential mathematicians of his time.
Hilbert discovered and developed a broad range of fundamental idea ...
(1862–1943) employed axiomatic reasoning in an attempt to provide a modern foundation of geometry.
Spaces and subspaces
Points
Points are generally considered fundamental objects for building geometry. They may be defined by the properties that they must have, as in Euclid's definition as "that which has no part",''Euclid's Elements – All thirteen books in one volume'', Based on Heath's translation, Green Lion Press . or insynthetic geometry
Synthetic geometry (sometimes referred to as axiomatic geometry or even pure geometry) is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulates ...
. In modern mathematics, they are generally defined as elements of a set
Set, The Set, SET or SETS may refer to:
Science, technology, and mathematics Mathematics
*Set (mathematics), a collection of elements
*Category of sets, the category whose objects and morphisms are sets and total functions, respectively
Electro ...
called space
Space is a three-dimensional continuum containing positions and directions. In classical physics, physical space is often conceived in three linear dimensions. Modern physicists usually consider it, with time, to be part of a boundless ...
, which is itself axiomatically defined.
With these modern definitions, every geometric shape is defined as a set of points; this is not the case in synthetic geometry, where a line is another fundamental object that is not viewed as the set of the points through which it passes.
However, there are modern geometries in which points are not primitive objects, or even without points. One of the oldest such geometries is Whitehead's point-free geometry
In mathematics, point-free geometry is a geometry whose primitive ontology, ontological notion is ''region (mathematics), region'' rather than point (geometry), point. Two axiomatic systems are set out below, one grounded in mereology, the other in ...
, formulated by Alfred North Whitehead
Alfred North Whitehead (15 February 1861 – 30 December 1947) was an English mathematician and philosopher. He created the philosophical school known as process philosophy, which has been applied in a wide variety of disciplines, inclu ...
in 1919–1920.
Lines
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
described a line as "breadthless length" which "lies equally with respect to the points on itself". In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coeffici ...
, but in a more abstract setting, such as incidence geometry
In mathematics, incidence geometry is the study of incidence structures. A geometric structure such as the Euclidean plane is a complicated object that involves concepts such as length, angles, continuity, betweenness, and incidence. An ''incide ...
, a line may be an independent object, distinct from the set of points which lie on it. In differential geometry, a geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
is a generalization of the notion of a line to curved spaces.
Planes
In Euclidean geometry a plane is a flat, two-dimensional surface that extends infinitely; the definitions for other types of geometries are generalizations of that. Planes are used in many areas of geometry. For instance, planes can be studied as a topological surface without reference to distances or angles; it can be studied as anaffine space
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties relat ...
, where collinearity and ratios can be studied but not distances; it can be studied as the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
using techniques of complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
; and so on.
Curves
Acurve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
is a 1-dimensional object that may be straight (like a line) or not; curves in 2-dimensional space are called plane curve
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane c ...
s and those in 3-dimensional space are called space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
s.
In topology, a curve is defined by a function from an interval of the real numbers to another space. In differential geometry, the same definition is used, but the defining function is required to be differentiable. Algebraic geometry studies algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
s, which are defined as algebraic varieties
Algebraic varieties are the central objects of study in algebraic geometry, a sub-field of mathematics. Classically, an algebraic variety is defined as the set of solutions of a system of polynomial equations over the real or complex numbers. ...
of dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
one.
Surfaces
surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
is a two-dimensional object, such as a sphere or paraboloid. In differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
and topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, surfaces are described by two-dimensional 'patches' (or neighborhoods
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neighbourh ...
) that are assembled by diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Definit ...
s or homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function ...
s, respectively. In algebraic geometry, surfaces are described by polynomial equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form P = 0, where ''P'' is a polynomial with coefficients in some field (mathematics), field, often the field of the rational numbers.
For example, x^5-3x+1=0 is a ...
s.
Solids
 A
A solid
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the ...
is a three-dimensional object bounded by a closed surface; for example, a ball
A ball is a round object (usually spherical, but sometimes ovoid) with several uses. It is used in ball games, where the play of the game follows the state of the ball as it is hit, kicked or thrown by players. Balls can also be used for s ...
is the volume bounded by a sphere.
Manifolds
Amanifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
is a generalization of the concepts of curve and surface. In topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, a manifold is a topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
where every point has a neighborhood
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neigh ...
that is homeomorphic
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function betw ...
to Euclidean space. In differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
, a differentiable manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One ...
is a space where each neighborhood is diffeomorphic
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.
Defini ...
to Euclidean space.
Manifolds are used extensively in physics, including in general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
and string theory
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and intera ...
.
Angles
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
defines a plane angle as the inclination to each other, in a plane, of two lines which meet each other, and do not lie straight with respect to each other. In modern terms, an angle is the figure formed by two rays, called the ''sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
The size of an angle is formalized as an angular measure
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing ...
.
In Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
, angles are used to study polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
s and triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
s, as well as forming an object of study in their own right. The study of the angles of a triangle or of angles in a unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
forms the basis of trigonometry
Trigonometry () is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle with ratios of its side lengths. The fiel ...
.
In differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
and calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, the angles between plane curve
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane c ...
s or space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
s or surfaces
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space.
Surface or surfaces may also refer to:
Mathematics
*Surface (mathematics), a generalization of a plane which needs not be flat
* Sur ...
can be calculated using the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
. Stewart, James (2012). ''Calculus: Early Transcendentals'', 7th ed., Brooks Cole Cengage Learning.
Measures: length, area, and volume
Length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, ...
, area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-di ...
, and volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
describe the size or extent of an object in one dimension, two dimension, and three dimensions respectively.
In Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
and analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
, the length of a line segment can often be calculated by the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
.
Area and volume can be defined as fundamental quantities separate from length, or they can be described and calculated in terms of lengths in a plane or 3-dimensional space. Mathematicians have found many explicit formulas for area and formulas for volume of various geometric objects. In calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, area and volume can be defined in terms of integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
s, such as the Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of Gö ...
or the Lebesgue integral
In mathematics, the integral of a non-negative Function (mathematics), function of a single variable can be regarded, in the simplest case, as the area between the Graph of a function, graph of that function and the axis. The Lebesgue integral, ...
.
Other geometrical measures include the curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
and compactness
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space. The idea is that a compact space has no "punctures" or "missing endpoints", i.e., it ...
.
Metrics and measures
 The concept of length or distance can be generalized, leading to the idea of
The concept of length or distance can be generalized, leading to the idea of metrics
Metric or metrical may refer to:
Measuring
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
...
. For instance, the Euclidean metric
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is oc ...
measures the distance between points in the Euclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
, while the hyperbolic metric measures the distance in the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
. Other important examples of metrics include the Lorentz metric of special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory of the relationship between Spacetime, space and time. In Albert Einstein's 1905 paper, Annus Mirabilis papers#Special relativity,
"On the Ele ...
and the semi-Riemannian metrics of general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
.
In a different direction, the concepts of length, area and volume are extended by measure theory, which studies methods of assigning a size or ''measure'' to Set (mathematics), sets, where the measures follow rules similar to those of classical area and volume.
Congruence and similarity
Congruence (geometry), Congruence and Similarity (geometry), similarity are concepts that describe when two shapes have similar characteristics. In Euclidean geometry, similarity is used to describe objects that have the same shape, while congruence is used to describe objects that are the same in both size and shape. Hilbert, in his work on creating a more rigorous foundation for geometry, treated congruence as an undefined term whose properties are defined byaxiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or ...
s.
Congruence and similarity are generalized in transformation geometry, which studies the properties of geometric objects that are preserved by different kinds of transformations.
Compass and straightedge constructions
Classical geometers paid special attention to constructing geometric objects that had been described in some other way. Classically, the only instruments used in most geometric constructions are the Compass (drafting), compass and ruler, straightedge. Also, every construction had to be complete in a finite number of steps. However, some problems turned out to be difficult or impossible to solve by these means alone, and ingenious constructions using Neusis construction, neusis, parabolas and other curves, or mechanical devices, were found.Rotation and orientation
The geometrical concepts of rotation and orientation define part of the placement of objects embedded in the plane or in space.Dimension
 Traditional geometry allowed dimensions 1 (a line or curve), 2 (a Plane (mathematics), plane or surface), and 3 (our ambient world conceived of as three-dimensional space). Furthermore, mathematicians and physicists have used higher dimensions for nearly two centuries. One example of a mathematical use for higher dimensions is the configuration space (physics), configuration space of a physical system, which has a dimension equal to the system's degrees of freedom. For instance, the configuration of a screw can be described by five coordinates.
In general topology, the concept of dimension has been extended from natural numbers, to infinite dimension (Hilbert spaces, for example) and positive real numbers (in fractal geometry). In
Traditional geometry allowed dimensions 1 (a line or curve), 2 (a Plane (mathematics), plane or surface), and 3 (our ambient world conceived of as three-dimensional space). Furthermore, mathematicians and physicists have used higher dimensions for nearly two centuries. One example of a mathematical use for higher dimensions is the configuration space (physics), configuration space of a physical system, which has a dimension equal to the system's degrees of freedom. For instance, the configuration of a screw can be described by five coordinates.
In general topology, the concept of dimension has been extended from natural numbers, to infinite dimension (Hilbert spaces, for example) and positive real numbers (in fractal geometry). In algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
, the dimension of an algebraic variety has received a number of apparently different definitions, which are all equivalent in the most common cases.
Symmetry
 The theme of
The theme of symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
in geometry is nearly as old as the science of geometry itself. Symmetric shapes such as the circle, regular polygons and platonic solids held deep significance for many ancient philosophers and were investigated in detail before the time of Euclid. Symmetric patterns occur in nature and were artistically rendered in a multitude of forms, including the graphics of Leonardo da Vinci, M. C. Escher, and others. In the second half of the 19th century, the relationship between symmetry and geometry came under intense scrutiny. Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
's Erlangen program proclaimed that, in a very precise sense, symmetry, expressed via the notion of a transformation group (mathematics), group, determines what geometry ''is''. Symmetry in classical Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
is represented by Congruence (geometry), congruences and rigid motions, whereas in projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
an analogous role is played by collineations, geometric transformations that take straight lines into straight lines. However it was in the new geometries of Bolyai and Lobachevsky, Riemann, William Kingdon Clifford, Clifford and Klein, and Sophus Lie that Klein's idea to 'define a geometry via its symmetry group' found its inspiration. Both discrete and continuous symmetries play prominent roles in geometry, the former in topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
and geometric group theory, the latter in Lie theory and Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as manifold, smooth manifolds with a ''Riemannian metric'' (an inner product on the tangent space at each point that varies smooth function, smo ...
.
A different type of symmetry is the principle of Duality (projective geometry), duality in projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
, among other fields. This meta-phenomenon can roughly be described as follows: in any theorem, exchange ''point'' with ''plane'', ''join'' with ''meet'', ''lies in'' with ''contains'', and the result is an equally true theorem. A similar and closely related form of duality exists between a vector space and its dual space.
Contemporary geometry
Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
is geometry in its classical sense. As it models the space of the physical world, it is used in many scientific areas, such as mechanics, astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, crystallography, and many technical fields, such as engineering, architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and construction, constructi ...
, geodesy, aerodynamics, and navigation. The mandatory educational curriculum of the majority of nations includes the study of Euclidean concepts such as point (geometry), points, Line (geometry), lines, plane (mathematics), planes, angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s, triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
s, congruence (geometry), congruence, similarity (geometry), similarity, solid figures, circles, and analytic geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and als ...
.
Euclidean vectors
Euclidean vectors are used for a myriad of applications in physics and engineering, such as position (geometry), position, displacement (geometry), displacement, deformation (physics), deformation, velocity, acceleration, force, etc.Differential geometry
calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
and linear algebra to study problems in geometry. It has applications in physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, econometrics, and bioinformatics, among others.
In particular, differential geometry is of importance to mathematical physics due to Albert Einstein's general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
postulation that the universe is curvature, curved. Differential geometry can either be ''intrinsic'' (meaning that the spaces it considers are smooth manifolds whose geometric structure is governed by a Riemannian metric, which determines how distances are measured near each point) or ''extrinsic'' (where the object under study is a part of some ambient flat Euclidean space).
Non-Euclidean geometry
Topology
 Topology is the field concerned with the properties of continuous mappings, and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as connectedness and compact (topology), compactness.
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are
Topology is the field concerned with the properties of continuous mappings, and can be considered a generalization of Euclidean geometry. In practice, topology often means dealing with large-scale properties of spaces, such as connectedness and compact (topology), compactness.
The field of topology, which saw massive development in the 20th century, is in a technical sense a type of transformation geometry, in which transformations are homeomorphism
In mathematics and more specifically in topology, a homeomorphism ( from Greek roots meaning "similar shape", named by Henri Poincaré), also called topological isomorphism, or bicontinuous function, is a bijective and continuous function ...
s. This has often been expressed in the form of the saying 'topology is rubber-sheet geometry'. Subfields of topology include geometric topology, differential topology, algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
and general topology.
Algebraic geometry
 Algebraic geometry is fundamentally the study by means of algebraic methods of some geometrical shapes, called algebraic sets, and defined as common zero of a function, zeros of multivariate polynomials. Algebraic geometry became an autonomous subfield of geometry , with a theorem called Hilbert's Nullstellensatz that establishes a strong correspondence between algebraic sets and ideal (ring theory), ideals of polynomial rings. This led to a parallel development of algebraic geometry, and its algebraic counterpart, called commutative algebra. From the late 1950s through the mid-1970s algebraic geometry had undergone major foundational development, with the introduction by Alexander Grothendieck of scheme theory, which allows using algebraic topology, topological methods, including cohomology theory, cohomology theories in a purely algebraic context. Scheme theory allowed to solve many difficult problems not only in geometry, but also in number theory. Wiles' proof of Fermat's Last Theorem is a famous example of a long-standing problem of number theory whose solution uses scheme theory and its extensions such as stack (mathematics), stack theory. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.
Algebraic geometry has applications in many areas, including cryptography and
Algebraic geometry is fundamentally the study by means of algebraic methods of some geometrical shapes, called algebraic sets, and defined as common zero of a function, zeros of multivariate polynomials. Algebraic geometry became an autonomous subfield of geometry , with a theorem called Hilbert's Nullstellensatz that establishes a strong correspondence between algebraic sets and ideal (ring theory), ideals of polynomial rings. This led to a parallel development of algebraic geometry, and its algebraic counterpart, called commutative algebra. From the late 1950s through the mid-1970s algebraic geometry had undergone major foundational development, with the introduction by Alexander Grothendieck of scheme theory, which allows using algebraic topology, topological methods, including cohomology theory, cohomology theories in a purely algebraic context. Scheme theory allowed to solve many difficult problems not only in geometry, but also in number theory. Wiles' proof of Fermat's Last Theorem is a famous example of a long-standing problem of number theory whose solution uses scheme theory and its extensions such as stack (mathematics), stack theory. One of seven Millennium Prize problems, the Hodge conjecture, is a question in algebraic geometry.
Algebraic geometry has applications in many areas, including cryptography and string theory
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and intera ...
.
Complex geometry
Complex geometry studies the nature of geometric structures modelled on, or arising out of, thecomplex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
. Complex geometry lies at the intersection of differential geometry, algebraic geometry, and analysis of several complex variables, and has found applications to string theory
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and intera ...
and Mirror symmetry (string theory), mirror symmetry.
Complex geometry first appeared as a distinct area of study in the work of Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
in his study of Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed vers ...
s. Work in the spirit of Riemann was carried out by the Italian school of algebraic geometry in the early 1900s. Contemporary treatment of complex geometry began with the work of Jean-Pierre Serre, who introduced the concept of sheaf (mathematics), sheaves to the subject, and illuminated the relations between complex geometry and algebraic geometry.
The primary objects of study in complex geometry are complex manifolds, complex algebraic varieties, and complex analytic varieties, and holomorphic vector bundles and coherent sheaves over these spaces. Special examples of spaces studied in complex geometry include Riemann surfaces, and Calabi–Yau manifolds, and these spaces find uses in string theory. In particular, worldsheets of strings are modelled by Riemann surfaces, and superstring theory predicts that the extra 6 dimensions of 10 dimensional spacetime may be modelled by Calabi–Yau manifolds.
Discrete geometry
Computational geometry
Computational geometry deals with algorithms and their implementation (computer science), implementations for manipulating geometrical objects. Important problems historically have included the travelling salesman problem, minimum spanning trees, hidden-line removal, and linear programming. Although being a young area of geometry, it has many applications in computer vision, image processing, computer-aided design, medical imaging, etc.Geometric group theory
Groups have been understood as geometric objects since Erlangen program, Klein's Erlangen programme. Geometric group theory studies Group action, group actions on objects that are regarded as geometric (significantly, isometric actions on Metric space, metric spaces) to study finitely generated groups, often involving large-scale geometric techniques and borrowing from topology, geometry, dynamics and analysis. It had a significant impact on low-dimensional topology, a celebrated result being Agol's proof of the virtually Haken conjecture that combines Geometrization conjecture, Perelman geometrization with Cubical complex, cubulation techniques. Group actions on their Cayley graph, Cayley graphs are foundational examples of isometric group actions. Other major topics include quasi-isometry, quasi-isometries, Gromov-hyperbolic groups and their generalizations (Relatively hyperbolic group, relatively and Acylindrically hyperbolic group, acylindrically hyperbolic groups), Free group, free groups and Out(Fn), their automorphisms, Bass–Serre theory, groups acting on trees, various notions of nonpositive curvature for groups (CAT(0) group, CAT(0) groups, Dehn function, Dehn functions, Automatic group, automaticity...), right angled Artin groups, and topics close to combinatorial group theory such as small cancellation theory and algorithmic problems (e.g. the Word problem for groups, word, Conjugacy problem, conjugacy, and Group isomorphism problem, isomorphism problems). Other group-theoretic topics like Mapping class group of a surface, mapping class groups, Kazhdan's property (T), property (T), Solvable group, solvability, Amenable group, amenability and Lattice (discrete subgroup), lattices in Lie groups are sometimes regarded as strongly geometric as well.Convex geometry
Convex geometry investigates convex set, convex shapes in the Euclidean space and its more abstract analogues, often using techniques of real analysis and discrete mathematics. It has close connections to convex analysis, optimization and functional analysis and important applications in number theory. Convex geometry dates back to antiquity.Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
gave the first known precise definition of convexity. The isoperimetric problem, a recurring concept in convex geometry, was studied by the Greeks as well, including Zenodorus (mathematician), Zenodorus. Archimedes, Plato, Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely domina ...
, and later Kepler and Coxeter all studied convex polytopes and their properties. From the 19th century on, mathematicians have studied other areas of convex mathematics, including higher-dimensional polytopes, volume and surface area of convex bodies, Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a smooth Surface (topology), surface in three-dimensional space at a point is the product of the principal curvatures, and , at the given point:
K = \kappa_1 \kappa_2.
For ...
, algorithms, tiling (geometry), tilings and lattice (group), lattices.
Applications
Geometry has found applications in many fields, some of which are described below.Art
 Mathematics and art are related in a variety of ways. For instance, the theory of perspective (graphical), perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of
Mathematics and art are related in a variety of ways. For instance, the theory of perspective (graphical), perspective showed that there is more to geometry than just the metric properties of figures: perspective is the origin of projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
.
Artists have long used concepts of proportionality (mathematics), proportion in design. Vitruvius developed a complicated theory of ''ideal proportions'' for the human figure. These concepts have been used and adapted by artists from Michelangelo to modern comic book artists.
The golden ratio is a particular proportion that has had a controversial role in art. Often claimed to be the most aesthetically pleasing ratio of lengths, it is frequently stated to be incorporated into famous works of art, though the most reliable and unambiguous examples were made deliberately by artists aware of this legend.
Tiling (geometry), Tilings, or tessellations, have been used in art throughout history. Islamic art makes frequent use of tessellations, as did the art of M. C. Escher. Escher's work also made use of hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
.
Cézanne advanced the theory that all images can be built up from the sphere, the cone, and the cylinder. This is still used in art theory today, although the exact list of shapes varies from author to author.
Architecture
Geometry has many applications in architecture. In fact, it has been said that geometry lies at the core of architectural design. Applications of geometry to architecture include the use ofprojective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
to create forced perspective, the use of conic sections in constructing domes and similar objects, the use of tessellations, and the use of symmetry.
Physics
The field ofastronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, especially as it relates to mapping the positions of stars and planets on the celestial sphere and describing the relationship between movements of celestial bodies, have served as an important source of geometric problems throughout history.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as manifold, smooth manifolds with a ''Riemannian metric'' (an inner product on the tangent space at each point that varies smooth function, smo ...
and pseudo-Riemannian geometry are used in general relativity
General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the differential geometry, geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of grav ...
. String theory makes use of several variants of geometry, as does quantum information theory.
Other fields of mathematics
René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
and the concurrent developments of algebra marked a new stage for geometry, since geometric figures such as plane curve
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane c ...
s could now be represented analytic geometry, analytically in the form of functions and equations. This played a key role in the emergence of infinitesimal calculus in the 17th century. Analytic geometry continues to be a mainstay of pre-calculus and calculus curriculum.
Another important area of application is number theory. In ancient Greece the Pythagoreans considered the role of numbers in geometry. However, the discovery of incommensurable lengths contradicted their philosophical views. Since the 19th century, geometry has been used for solving problems in number theory, for example through the geometry of numbers or, more recently, scheme theory, which is used in Wiles's proof of Fermat's Last Theorem.
See also
;Lists * List of geometers ** :Algebraic geometers ** :Differential geometers ** :Geometers ** :Topologists * List of formulas in elementary geometry * List of geometry topics * List of important publications in mathematics#Geometry, List of important publications in geometry * Lists of mathematics topics ;Related topics * Descriptive geometry * ''Flatland'', a book written by Edwin Abbott Abbott about two- and three-dimensional space, to understand the concept of four dimensions * List of interactive geometry software ;Other applications * Molecular geometryNotes
References
Sources
* * * *Further reading
* * *External links
* * A v:Geometry, geometry course from v:, Wikiversity''Unusual Geometry Problems''
''The Math Forum'' – Geometry
*
*
*
Nature Precedings – ''Pegs and Ropes Geometry at Stonehenge''
* [https://web.archive.org/web/20071004174210/http://www.gresham.ac.uk/event.asp?PageId=45&EventId=618 "4000 Years of Geometry"], lecture by Robin Wilson given at Gresham College, 3 October 2007 (available for MP3 and MP4 download as well as a text file) *
Finitism in Geometry
at the Stanford Encyclopedia of Philosophy
Interactive geometry reference with hundreds of applets
Geometry classes
at Khan Academy {{Authority control Geometry,