geodetic precession

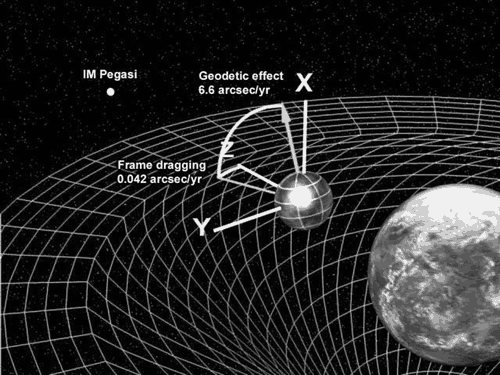The geodetic effect (also known as geodetic precession, de Sitter precession or de Sitter effect) represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body. For example, the vector could be the angular momentum of a gyroscope orbiting the Earth, as carried out by the Gravity Probe B experiment. The geodetic effect was first predicted by Willem de Sitter in 1916, who provided relativistic corrections to the Earth–Moon system's motion. De Sitter's work was extended in 1918 by Jan Schouten and in 1920 by Adriaan Fokker. It can also be applied to a particular secular precession of astronomical orbits, equivalent to the rotation of the Laplace–Runge–Lenz vector.

The term geodetic effect has two slightly different meanings as the moving body may be spinning or non-spinning. Non-spinning bodies move in geodesics, whereas spinning bodies move in slightly different orbits.

The difference between de Sitter precession and Lense–Thirring precession (frame dragging) is that the de Sitter effect is due simply to the presence of a central mass, whereas Lense–Thirring precession is due to the rotation of the central mass. The total precession is calculated by combining the de Sitter precession with the Lense–Thirring precession.

Experimental confirmation

The geodetic effect was verified to a precision of better than 0.5% percent by Gravity Probe B, an experiment which measures the tilting of the spin axis of gyroscopes in orbit about the Earth. The first results were announced on April 14, 2007, at the meeting of the American Physical Society.

Formulae

To derive the precession, assume the system is in a rotating Schwarzschild metric. The nonrotating metric is

:$ds^2 = dt^2 \left(1-\frac\right) - dr^2 \left(1 - \frac\right)^ - r^2 (d\theta^2 + \sin^2 \theta \, d\phi'^2) ,$

where ''c'' = ''G'' = 1.

We introduce a rotating coordinate system, with an angular velocity $\omega$, such that a satellite in a circular orbit in the θ = π/2 plane remains at rest. This gives us

:$d\phi = d\phi' - \omega \, dt.$

In this coordinate system, an observer at radial position ''r'' sees a vector positioned at ''r'' as rotating with angular frequency ω. This observer, however, sees a vector positioned at some other value of ''r'' as rotating at a different rate, due to relativistic time dilation. Transforming the Schwarzschild metric into the rotating frame, and assuming that $\theta$ is a constant, we find

:$\begin ds^2 & = \left(1-\frac-r^2 \beta\omega^2 \right)\left(dt-\frac \, d\phi\right)^2 - \\ & - dr^2 \left(1-\frac\right)^ - \frac \, d\phi^2, \end$

with $\beta = \sin^2(\theta)$. For a body orbiting in the θ = π/2 plane, we will have β = 1, and the body's world-line will maintain constant spatial coordinates for all time. Now, the metric is in the canonical form

:$ds^2 = e^\left(dt - w_i \, dx^i \right)^2 - k_ \, dx^i \, dx^j.$

From this canonical form, we can easily determine the rotational rate of a gyroscope in proper time

:
\begin
\Omega & = \frac e^\Phi ^k^(\omega_-\omega_)(\omega_ - \omega_) = \\
& = \frac = \sqrt\omega.
\end

where the last equality is true only for free falling observers for which
there is no acceleration, and thus $\Phi,_ = 0$. This leads to

:$\Phi,_i = \frac = 0.$

Solving this equation for ω yields

:$\omega^2 = \frac.$

This is essentially Kepler's law of periods, which happens to be relativistically exact when expressed in terms of the time coordinate ''t'' of this particular rotating coordinate system. In the rotating frame, the satellite remains at rest, but an observer aboard the satellite sees the gyroscope's angular momentum vector precessing at the rate ω. This observer also sees the distant stars as rotating, but they rotate at a slightly different rate due to time dilation. Let τ be the gyroscope's proper time. Then

:$\Delta \tau = \left(1-\frac - r^2 \beta\omega^2 \right)^ \, dt = \left(1-\frac\right)^ \, dt.$

The −2''m''/''r'' term is interpreted as the gravitational time dilation, while the additional −''m''/''r'' is due to the rotation of this frame of reference. Let α' be the accumulated precession in the rotating frame. Since $\alpha' = \Omega \Delta \tau$, the precession over the course of one orbit, relative to the distant stars, is given by:

:$\alpha = \alpha' + 2\pi = -2 \pi \sqrt\Bigg( \left(1-\frac \right)^ - 1 \Bigg).$

With a first-order Taylor series we find

:$\alpha \approx \frac\sqrt = \frac\sin(\theta).$

Thomas precession

One can attempt to break down the de Sitter precession into a kinematic effect called Thomas precession combined with a geometric effect caused by gravitationally curved spacetime. At least one author does describe it this way, but others state that "The Thomas precession comes into play for a gyroscope on the surface of the Earth ..., but not for a gyroscope in a freely moving satellite." An objection to the former interpretation is that the Thomas precession required has the wrong sign. The Fermi-Walker transport equationMisner, Thorne, and Wheeler, Gravitation, p. 165, pp. 175-176, pp. 1117-1121 gives both the geodetic effect and Thomas precession and describes the transport of the spin 4-vector for accelerated motion in curved spacetime. The spin 4-vector is orthogonal to the velocity 4-vector. Fermi-Walker transport preserves this relation. If there is no acceleration, Fermi-Walker transport is just parallel transport along a geodesic and gives the spin precession due to the geodetic effect. For the acceleration due to uniform circular motion in flat Minkowski spacetime, Fermi Walker transport gives the Thomas precession.

See also

* Frame-dragging
* Geodesics in general relativity
* Gravity well
* Timeline of gravitational physics and relativity

Notes

References

* Wolfgang Rindler (2006) Relativity: special, general, and cosmological (2nd Ed.), Oxford University Press,

External links

* Gravity Probe B websites a
NASA
an
Stanford University





{{Relativity

General relativity