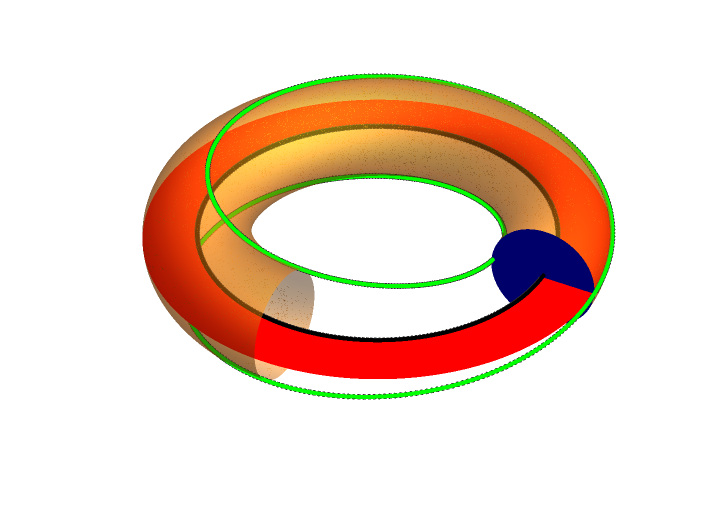In magnetic confinement fusion, a flux surface is a surface on which magnetic field lines lie. Since the

magnetic field A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and to ...

is divergence-free (and magnetic nulls are undesirable), the Poincare-Hopf theorem implies that such a surface must be either a torus, or a knot. In the tokamak and the stellarator flux surfaces have toroidal shapes, whereas the more exotic knotatron has a knotted flux surface. Flux surfaces are typically characterized the poloidal

magnetic flux In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted or . The SI unit of magnetic flux is the weber ( ...

or the toroidal magnetic flux. The poloidal flux is the magnetic flux passing through a ribbon going from the magnetic axis (the centre of the device) to the flux surface, and the toroidal flux is the magnetic flux passing through a circle which encloses the magnetic axis. The total flux passing through flux surface itself is zero, as magnetic field lines are everywhere tangent to the surface. Flux surfaces can either be rational or irrational, depending on the behavior of magnetic field lines on the flux surface. Rational surfaces have magnetic field lines are which are periodic; the magnetic field line closes back on itself. Conversely irrational surfaces have magnetic field lines which do not close back on themselves, and a magnetic field line traces out the entire flux surface (the magnetic field line comes arbitrarily close to each point on the flux surface). Rational magnetic surfaces are very sensitive to perturbations and can degenerate into magnetic islands. Flux surfaces are not guaranteed to exist; the magnetic field line can fill a volume chaotically. The theory of magnetic field lines in toroidal systems is closely related to the theory of 2-dimensional Hamiltonian systems.

References

{{Reflist Magnetic confinement fusion