Euclidean relation on:
[Wikipedia]
[Google]
[Amazon]
In
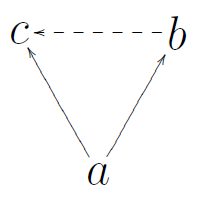 A
A
 # Due to the commutativity of ∧ in the definition's antecedent, ''aRb'' ∧ ''aRc'' even implies ''bRc'' ∧ ''cRb'' when ''R'' is right Euclidean. Similarly, ''bRa'' ∧ ''cRa'' implies ''bRc'' ∧ ''cRb'' when ''R'' is left Euclidean.
# The property of being Euclidean is different from transitivity. For example, ≤ is transitive, but not right Euclidean, while ''xRy'' defined by 0 ≤ ''x'' ≤ ''y'' + 1 ≤ 2 is not transitive, but right Euclidean on
# Due to the commutativity of ∧ in the definition's antecedent, ''aRb'' ∧ ''aRc'' even implies ''bRc'' ∧ ''cRb'' when ''R'' is right Euclidean. Similarly, ''bRa'' ∧ ''cRa'' implies ''bRc'' ∧ ''cRb'' when ''R'' is left Euclidean.
# The property of being Euclidean is different from transitivity. For example, ≤ is transitive, but not right Euclidean, while ''xRy'' defined by 0 ≤ ''x'' ≤ ''y'' + 1 ≤ 2 is not transitive, but right Euclidean on
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, Euclidean relations are a class of binary relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs ...
s that formalize " Axiom 1" in Euclid's ''Elements'': "Magnitudes which are equal to the same are equal to each other."
Definition
binary relation
In mathematics, a binary relation associates some elements of one Set (mathematics), set called the ''domain'' with some elements of another set called the ''codomain''. Precisely, a binary relation over sets X and Y is a set of ordered pairs ...
''R'' on a set
Set, The Set, SET or SETS may refer to:
Science, technology, and mathematics Mathematics
*Set (mathematics), a collection of elements
*Category of sets, the category whose objects and morphisms are sets and total functions, respectively
Electro ...
''X'' is Euclidean (sometimes called right Euclidean) if it satisfies the following: for every ''a'', ''b'', ''c'' in ''X'', if ''a'' is related to ''b'' and ''c'', then ''b'' is related to ''c''.. To write this in predicate logic
First-order logic, also called predicate logic, predicate calculus, or quantificational logic, is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables ove ...
:
:
Dually, a relation ''R'' on ''X'' is left Euclidean if for every ''a'', ''b'', ''c'' in ''X'', if ''b'' is related to ''a'' and ''c'' is related to ''a'', then ''b'' is related to ''c'':
:
Properties
natural number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ...
s.
# For symmetric relation
A symmetric relation is a type of binary relation. Formally, a binary relation ''R'' over a set ''X'' is symmetric if:
: \forall a, b \in X(a R b \Leftrightarrow b R a) ,
where the notation ''aRb'' means that .
An example is the relation "is equ ...
s, transitivity, right Euclideanness, and left Euclideanness all coincide. However, a non-symmetric relation can also be both transitive and right Euclidean, for example, ''xRy'' defined by ''y''=0.
# A relation that is both right Euclidean and reflexive is also symmetric and therefore an equivalence relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric, and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation. A simpler example is equ ...
. Similarly, each left Euclidean and reflexive relation is an equivalence.
# The range of a right Euclidean relation is always a subset of its domain. The restriction of a right Euclidean relation to its range is always reflexive, and therefore an equivalence. Similarly, the domain of a left Euclidean relation is a subset of its range, and the restriction of a left Euclidean relation to its domain is an equivalence. Therefore, a right Euclidean relation on ''X'' that is also right total (respectively a left Euclidean relation on ''X'' that is also left total) is an equivalence, since its range (respectively its domain) is ''X''..
# A relation ''R'' is both left and right Euclidean, if, and only if, the domain and the range set of ''R'' agree, and ''R'' is an equivalence relation on that set.
# A right Euclidean relation is always quasitransitive, as is a left Euclidean relation.
# A connected right Euclidean relation is always transitive; and so is a connected left Euclidean relation.
# If ''X'' has at least 3 elements, a connected right Euclidean relation ''R'' on ''X'' cannot be antisymmetric, and neither can a connected left Euclidean relation on ''X''. On the 2-element set ''X'' = , e.g. the relation ''xRy'' defined by ''y''=1 is connected, right Euclidean, and antisymmetric, and ''xRy'' defined by ''x''=1 is connected, left Euclidean, and antisymmetric.
# A relation ''R'' on a set ''X'' is right Euclidean if, and only if, the restriction ''R'' := ''R''ran(''R'') is an equivalence and for each ''x'' in ''X''\ran(''R''), all elements to which ''x'' is related under ''R'' are equivalent under ''R''. Similarly, ''R'' on ''X'' is left Euclidean if, and only if, ''R'' := ''R''dom(''R'') is an equivalence and for each ''x'' in ''X''\dom(''R''), all elements that are related to ''x'' under ''R'' are equivalent under ''R''.
# A left Euclidean relation is left-unique if, and only if, it is antisymmetric. Similarly, a right Euclidean relation is right unique if, and only if, it is anti-symmetric.
# A left Euclidean and left unique relation is vacuously transitive, and so is a right Euclidean and right unique relation.
# A left Euclidean relation is left quasi-reflexive. For left-unique relations, the converse also holds. Dually, each right Euclidean relation is right quasi-reflexive, and each right unique and right quasi-reflexive relation is right Euclidean. Lemma 44-46.
References
{{reflist Properties of binary relations Relation