eccentricity (orbit)

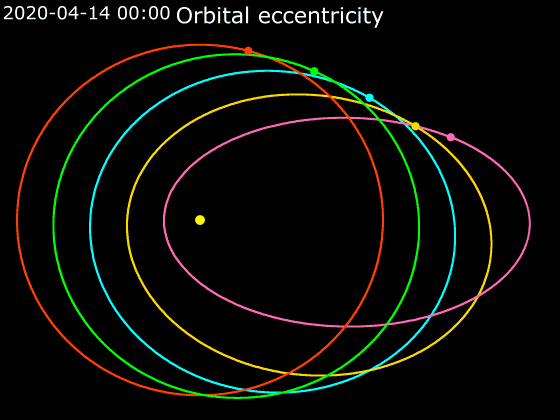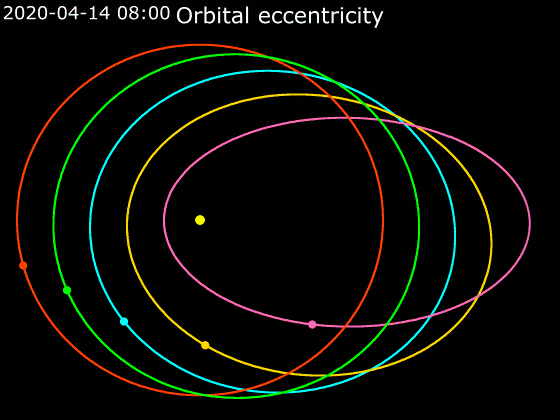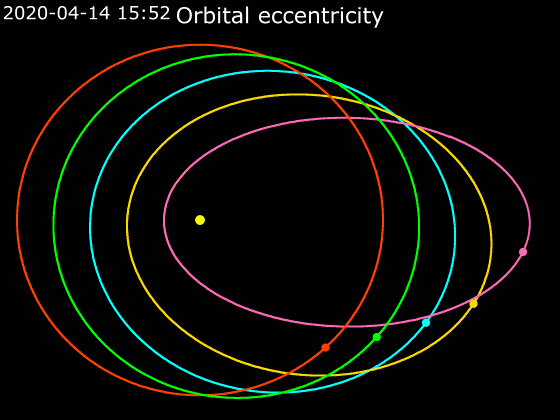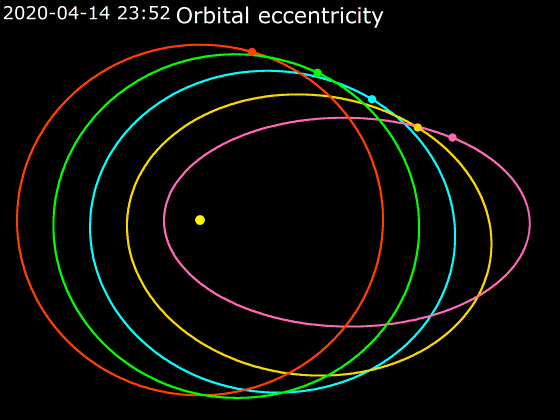In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy.

Definition

In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape.

The eccentricity may take the following values:
* Circular orbit:
* Elliptic orbit:
* Parabolic trajectory:
* Hyperbolic trajectory:

The eccentricity is given by

$e = \sqrt$

where is the total orbital energy, is the angular momentum, is the reduced mass, and $\alpha$ the coefficient of the inverse-square law central force such as in the theory of gravity or electrostatics in classical physics:
$F = \frac$
($\alpha$ is negative for an attractive force, positive for a repulsive one; related to the Kepler problem)

or in the case of a gravitational force:
$e = \sqrt$

where is the specific orbital energy (total energy divided by the reduced mass), the standard gravitational parameter based on the total mass, and the specific relative angular momentum (angular momentum divided by the reduced mass).

For values of from to just under the orbit's shape is an increasingly elongated (or flatter) ellipse; for values of just over to infinity the orbit is a hyperbola branch making a total turn of decreasing from 180 to 0 degrees. Here, the total turn is analogous to turning number, but for open curves (an angle covered by velocity vector). The limit case between an ellipse and a hyperbola, when equals , is parabola.

Radial trajectories are classified as elliptic, parabolic, or hyperbolic based on the energy of the orbit, not the eccentricity. Radial orbits have zero angular momentum and hence eccentricity equal to one. Keeping the energy constant and reducing the angular momentum, elliptic, parabolic, and hyperbolic orbits each tend to the corresponding type of radial trajectory while tends to (or in the parabolic case, remains ).

For a repulsive force only the hyperbolic trajectory, including the radial version, is applicable.

For elliptical orbits, a simple proof shows that $\ \arcsin(e)\$ gives the projection angle of a perfect circle to an ellipse of eccentricity . For example, to view the eccentricity of the planet Mercury (), one must simply calculate the inverse sine to find the projection angle of 11.86 degrees. Then, tilting any circular object by that angle, the apparent ellipse of that object projected to the viewer's eye will be of the same eccentricity.

Etymology

The word "eccentricity" comes from Medieval Latin ''eccentricus'', derived from Greek ''ekkentros'' "out of the center", from ''ek-'', "out of" + ''kentron'' "center". "Eccentric" first appeared in English in 1551, with the definition "...a circle in which the earth, sun. etc. deviates from its center". In 1556, five years later, an adjectival form of the word had developed.

Calculation

The eccentricity of an orbit can be calculated from the orbital state vectors as the magnitude of the eccentricity vector:
$e = \left , \mathbf \right ,$
where:
* is the eccentricity vector (''"Hamilton's vector"'').

For elliptical orbits it can also be calculated from the periapsis and apoapsis since $r_\text = a \, (1 - e )$ and $r_\text = a \, (1 + e )\,,$ where is the length of the semi-major axis.$\begin e &= \frac \\ \, \\ &= \frac \\ \, \\ &= 1 - \frac \end$
where:
* is the radius at apoapsis (also "apofocus", "aphelion", "apogee"), i.e., the farthest distance of the orbit to the center of mass of the system, which is a focus of the ellipse.
* is the radius at periapsis (or "perifocus" etc.), the closest distance.

The semi-major axis, a, is also the path-averaged distance to the centre of mass, while the time-averaged distance is a(1 + e e / 2


The eccentricity of an elliptical orbit can be used to obtain the ratio of the apoapsis radius to the periapsis radius:
$\frac = \frac = \frac$

For Earth, orbital eccentricity , apoapsis is aphelion and periapsis is perihelion, relative to the Sun.

For Earth's annual orbit path, the ratio of longest radius () / shortest radius () is $\frac = \frac \text$

Examples

The table lists the values for all planets and dwarf planets, and selected asteroids, comets, and moons. Mercury (planet), Mercury has the greatest orbital eccentricity of any planet in the Solar System (''e'' = ), followed by Mars of . Such eccentricity is sufficient for Mercury to receive twice as much solar irradiation at perihelion compared to aphelion. Before its demotion from planet status in 2006, Pluto was considered to be the planet with the most eccentric orbit (''e'' = ). Other Trans-Neptunian objects have significant eccentricity, notably the dwarf planet Eris (0.44). Even further out, Sedna has an extremely-high eccentricity of due to its estimated aphelion of 937 AU and perihelion of about 76 AU, possibly under influence of unknown object(s).

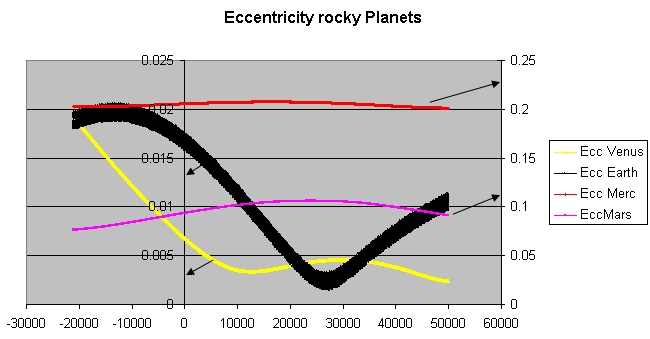
The eccentricity of Earth's orbit is currently about ; its orbit is nearly circular. Neptune's and Venus's have even lower eccentricities of and respectively, the latter being the least orbital eccentricity of any planet in the Solar System. Over hundreds of thousands of years, the eccentricity of the Earth's orbit varies from nearly to almost 0.058 as a result of gravitational attractions among the planets.

Luna's value is , the most eccentric of the large moons in the Solar System. The four Galilean moons ( Io, Europa, Ganymede and Callisto) have their eccentricities of less than 0.01. Neptune's largest moon Triton has an eccentricity of (), the smallest eccentricity of any known moon in the Solar System; its orbit is as close to a perfect circle as can be currently measured. Smaller moons, particularly irregular moons, can have significant eccentricities, such as Neptune's third largest moon, Nereid, of .

Most of the Solar System's asteroids have orbital eccentricities between 0 and 0.35 with an average value of 0.17. Their comparatively high eccentricities are probably due to under influence of Jupiter and to past collisions.

Comets have very different values of eccentricities. Periodic comets have eccentricities mostly between 0.2 and 0.7,
but some of them have highly eccentric elliptical orbits with eccentricities just below 1; for example, Halley's Comet has a value of 0.967. Non-periodic comets follow near- parabolic orbits and thus have eccentricities even closer to 1. Examples include Comet Hale–Bopp with a value of , Comet Ikeya-Seki with a value of and Comet McNaught (C/2006 P1) with a value of . As first two's values are less than 1, their orbit are elliptical and they will return.
McNaught has a hyperbolic orbit but within the influence of the inner planets, is still bound to the Sun with an orbital period of about 10⁵ years. Comet C/1980 E1 has the largest eccentricity of any known hyperbolic comet of solar origin with an eccentricity of 1.057, and will eventually leave the Solar System.

Oumuamua is the first interstellar object to be found passing through the Solar System. Its orbital eccentricity of 1.20 indicates that Oumuamua has never been gravitationally bound to the Sun. It was discovered 0.2 AU ( km;  mi) from Earth and is roughly 200 meters in diameter. It has an interstellar speed (velocity at infinity) of 26.33 km/s ( mph).

The exoplanet HD 20782 b has the most eccentric orbit known of 0.97 ± 0.01, followed by HD 80606 b of 0.93226 .

Mean average

The mean eccentricity of an object is the average eccentricity as a result of perturbations over a given time period. For example: Neptune currently has an instant (current epoch) eccentricity of , but from 1800 to 2050 has a mean eccentricity of .

Climatic effect

Orbital mechanics require that the duration of the seasons be proportional to the area of Earth's orbit swept between the solstices and equinoxes, so when the orbital eccentricity is extreme, the seasons that occur on the far side of the orbit ( aphelion) can be substantially longer in duration. Northern hemisphere autumn and winter occur at closest approach ( perihelion), when Earth is moving at its maximum velocity—while the opposite occurs in the southern hemisphere. As a result, in the northern hemisphere, autumn and winter are slightly shorter than spring and summer—but in global terms this is balanced with them being longer below the equator. In 2006, the northern hemisphere summer was 4.66 days longer than winter, and spring was 2.9 days longer than autumn due to orbital eccentricity.

Apsidal precession also slowly changes the place in Earth's orbit where the solstices and equinoxes occur. This is a slow change in the orbit of Earth, not the axis of rotation, which is referred to as axial precession. The climatic effects of this change are part of the Milankovitch cycles. Over the next years, the northern hemisphere winters will become gradually longer and summers will become shorter. Any cooling effect in one hemisphere is balanced by warming in the other, and any overall change will be counteracted by the fact that the eccentricity of Earth's orbit will be almost halved. This will reduce the mean orbital radius and raise temperatures in both hemispheres closer to the mid-interglacial peak.

Exoplanets

Of the many exoplanets discovered, most have a higher orbital eccentricity than planets in the Solar System. Exoplanets found with low orbital eccentricity (near-circular orbits) are very close to their star and are tidally-locked to the star. All eight planets in the Solar System have near-circular orbits. The exoplanets discovered show that the Solar System, with its unusually-low eccentricity, is rare and unique. One theory attributes this low eccentricity to the high number of planets in the Solar System; another suggests it arose because of its unique asteroid belts. A few other multiplanetary systems have been found, but none resemble the Solar System. The Solar System has unique planetesimal systems, which led the planets to have near-circular orbits. Solar planetesimal systems include the asteroid belt, Hilda family, Kuiper belt, Hills cloud, and the Oort cloud. The exoplanet systems discovered have either no planetesimal systems or a very large one. Low eccentricity is needed for habitability, especially advanced life. High multiplicity planet systems are much more likely to have habitable exoplanets. The grand tack hypothesis of the Solar System also helps understand its near-circular orbits and other unique features.

See also

* Equation of time

Footnotes

References

Further reading

*

External links

World of Physics: Eccentricity


includes (calculated) data from tp://ftp.ncdc.noaa.gov/pub/data/paleo/insolation/ Berger (1978), Berger and Loutre (1991)br>Laskar et al. (2004)
on Earth orbital variations, Includes eccentricity over the last 50 million years and for the coming 20 million years.

The orbital simulations by Varadi, Ghil and Runnegar (2003)
provides series for Earth orbital eccentricity and orbital inclination.

{{Use dmy dates, date=December 2022

Orbits