Earth's Figure on:
[Wikipedia]
[Google]
[Amazon]
In
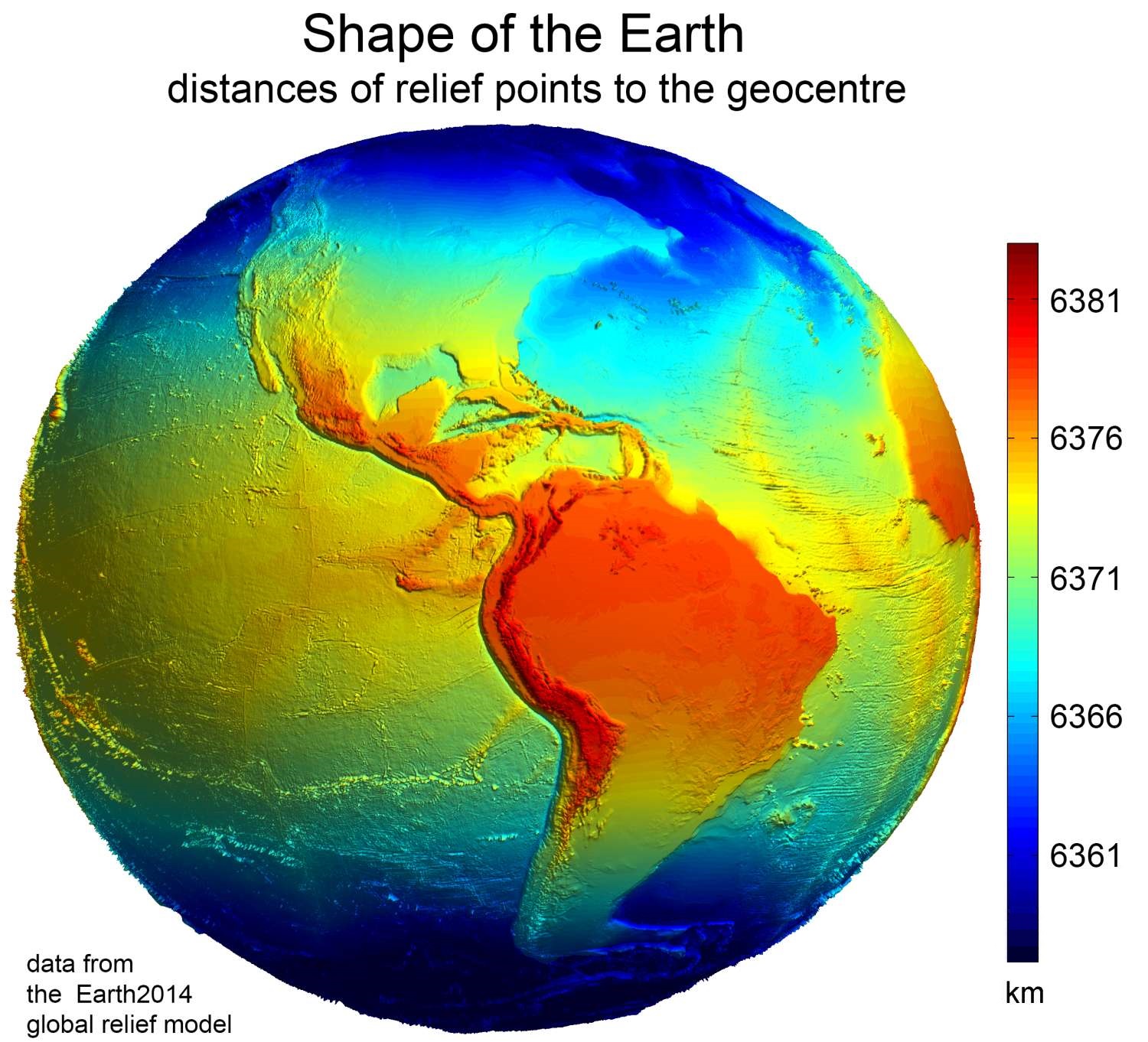 By the late 1600s, serious effort was devoted to modeling the Earth as an ellipsoid, beginning with French astronomer Jean Picard's measurement of a degree of arc along the Paris meridian. Improved maps and better measurement of distances and areas of national territories motivated these early attempts. Surveying instrumentation and techniques improved over the ensuing centuries. Models for the figure of the Earth improved in step.
In the mid- to late 20th century, research across the geosciences contributed to drastic improvements in the accuracy of the figure of the Earth. The primary utility of this improved accuracy was to provide geographical and gravitational data for the inertial guidance systems of ballistic missiles. This funding also drove the expansion of geoscientific disciplines, fostering the creation and growth of various geoscience departments at many universities. These developments benefited many civilian pursuits as well, such as weather and communication
By the late 1600s, serious effort was devoted to modeling the Earth as an ellipsoid, beginning with French astronomer Jean Picard's measurement of a degree of arc along the Paris meridian. Improved maps and better measurement of distances and areas of national territories motivated these early attempts. Surveying instrumentation and techniques improved over the ensuing centuries. Models for the figure of the Earth improved in step.
In the mid- to late 20th century, research across the geosciences contributed to drastic improvements in the accuracy of the figure of the Earth. The primary utility of this improved accuracy was to provide geographical and gravitational data for the inertial guidance systems of ballistic missiles. This funding also drove the expansion of geoscientific disciplines, fostering the creation and growth of various geoscience departments at many universities. These developments benefited many civilian pursuits as well, such as weather and communication

 As theorized by
As theorized by
 Modern geodesy tends to retain the ellipsoid of revolution as a reference ellipsoid and treat triaxiality and pear shape as a part of the geoid figure: they are represented by the spherical harmonic coefficients and , respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.
It was stated earlier that measurements are made on the apparent or topographic surface of the Earth and it has just been explained that computations are performed on an ellipsoid. One other surface is involved in geodetic measurement: the geoid. In geodetic surveying, the computation of the geodetic coordinates of points is commonly performed on a reference ellipsoid closely approximating the size and shape of the Earth in the area of the survey. The actual measurements made on the surface of the Earth with certain instruments are however referred to the geoid. The ellipsoid is a mathematically defined regular surface with specific dimensions. The geoid, on the other hand, coincides with that surface to which the oceans would conform over the entire Earth if free to adjust to the combined effect of the Earth's mass attraction (
Modern geodesy tends to retain the ellipsoid of revolution as a reference ellipsoid and treat triaxiality and pear shape as a part of the geoid figure: they are represented by the spherical harmonic coefficients and , respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.
It was stated earlier that measurements are made on the apparent or topographic surface of the Earth and it has just been explained that computations are performed on an ellipsoid. One other surface is involved in geodetic measurement: the geoid. In geodetic surveying, the computation of the geodetic coordinates of points is commonly performed on a reference ellipsoid closely approximating the size and shape of the Earth in the area of the survey. The actual measurements made on the surface of the Earth with certain instruments are however referred to the geoid. The ellipsoid is a mathematically defined regular surface with specific dimensions. The geoid, on the other hand, coincides with that surface to which the oceans would conform over the entire Earth if free to adjust to the combined effect of the Earth's mass attraction (
 The local tangent plane is appropriate for analysis across small distances.
The local tangent plane is appropriate for analysis across small distances.
 The best local spherical approximation to the ellipsoid in the vicinity of a given point is the ''Earth's osculating sphere''. Its radius equals Earth's Gaussian radius of curvature, and its radial direction coincides with the geodetic normal direction. The center of the osculating sphere is offset from the center of the ellipsoid, but is at the center of curvature for the given point on the ellipsoid surface. This concept aids the interpretation of terrestrial and planetary radio occultation
The best local spherical approximation to the ellipsoid in the vicinity of a given point is the ''Earth's osculating sphere''. Its radius equals Earth's Gaussian radius of curvature, and its radial direction coincides with the geodetic normal direction. The center of the osculating sphere is offset from the center of the ellipsoid, but is at the center of curvature for the given point on the ellipsoid surface. This concept aids the interpretation of terrestrial and planetary radio occultation
Reference Ellipsoids (PCI Geomatics)Reference Ellipsoids (ScanEx)
Jos Leys "The shape of Planet Earth"
{{Authority control Earth Geodesy Geophysics
geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
, the figure of the Earth is the size and shape used to model planet Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
. The kind of figure depends on application, including the precision needed for the model. A spherical Earth
Spherical Earth or Earth's curvature refers to the approximation of the figure of the Earth as a sphere. The earliest documented mention of the concept dates from around the 5th century BC, when it appears in the writings of Ancient Greek philos ...
is a well-known historical approximation that is satisfactory for geography
Geography (from Ancient Greek ; combining 'Earth' and 'write', literally 'Earth writing') is the study of the lands, features, inhabitants, and phenomena of Earth. Geography is an all-encompassing discipline that seeks an understanding o ...
, astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
and many other purposes. Several models with greater accuracy (including ellipsoid) have been developed so that coordinate systems can serve the precise needs of navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navig ...
, surveying
Surveying or land surveying is the technique, profession, art, and science of determining the land, terrestrial Plane (mathematics), two-dimensional or Three-dimensional space#In Euclidean geometry, three-dimensional positions of Point (geom ...
, cadastre
A cadastre or cadaster ( ) is a comprehensive recording of the real estate or real property's metes-and-bounds of a country.Jo Henssen, ''Basic Principles of the Main Cadastral Systems in the World,'/ref>
Often it is represented graphically in ...
, land use, and various other concerns.
Motivation
Earth's topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, hydrographers, and geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely complicated. The Pythagorean concept of aspherical Earth
Spherical Earth or Earth's curvature refers to the approximation of the figure of the Earth as a sphere. The earliest documented mention of the concept dates from around the 5th century BC, when it appears in the writings of Ancient Greek philos ...
offers a simple surface that is easy to deal with mathematically. Many astronomical and navigational computations use a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
to model the Earth as a close approximation. However, a more accurate figure is needed for measuring distances and areas on the scale beyond the purely local. Better approximations can be made by modeling the entire surface as an oblate spheroid, using spherical harmonics to approximate the geoid, or modeling a region with a best-fit reference ellipsoid.
For surveys of small areas, a planar (flat) model of Earth's surface suffices because the local topography overwhelms the curvature. Plane-table surveys are made for relatively small areas without considering the size and shape of the entire Earth. A survey of a city, for example, might be conducted this way.
 By the late 1600s, serious effort was devoted to modeling the Earth as an ellipsoid, beginning with French astronomer Jean Picard's measurement of a degree of arc along the Paris meridian. Improved maps and better measurement of distances and areas of national territories motivated these early attempts. Surveying instrumentation and techniques improved over the ensuing centuries. Models for the figure of the Earth improved in step.
In the mid- to late 20th century, research across the geosciences contributed to drastic improvements in the accuracy of the figure of the Earth. The primary utility of this improved accuracy was to provide geographical and gravitational data for the inertial guidance systems of ballistic missiles. This funding also drove the expansion of geoscientific disciplines, fostering the creation and growth of various geoscience departments at many universities. These developments benefited many civilian pursuits as well, such as weather and communication
By the late 1600s, serious effort was devoted to modeling the Earth as an ellipsoid, beginning with French astronomer Jean Picard's measurement of a degree of arc along the Paris meridian. Improved maps and better measurement of distances and areas of national territories motivated these early attempts. Surveying instrumentation and techniques improved over the ensuing centuries. Models for the figure of the Earth improved in step.
In the mid- to late 20th century, research across the geosciences contributed to drastic improvements in the accuracy of the figure of the Earth. The primary utility of this improved accuracy was to provide geographical and gravitational data for the inertial guidance systems of ballistic missiles. This funding also drove the expansion of geoscientific disciplines, fostering the creation and growth of various geoscience departments at many universities. These developments benefited many civilian pursuits as well, such as weather and communication satellite
A satellite or an artificial satellite is an object, typically a spacecraft, placed into orbit around a celestial body. They have a variety of uses, including communication relay, weather forecasting, navigation ( GPS), broadcasting, scient ...
control and GPS location-finding, which would be impossible without highly accurate models for the figure of the Earth.
Models
The models for the figure of the Earth vary in the way they are used, in their complexity, and in the accuracy with which they represent the size and shape of the Earth.Sphere
The simplest model for the shape of the entire Earth is a sphere. The Earth'sradius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
is the distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
from Earth's center to its surface, about . While "radius" normally is a characteristic of perfect spheres, the Earth deviates from spherical by only a third of a percent, sufficiently close to treat it as a sphere in many contexts and justifying the term "the radius of the Earth".
The concept of a spherical Earth dates back to around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC
The 3rd century BC started the first day of 300 BC and ended the last day of 201 BC. It is considered part of the Classical antiquity, Classical Era, Epoch (reference date), epoch, or historical period.
In the Mediterranean Basin, the first fe ...
. The first scientific estimation of the radius of the Earth was given by Eratosthenes about 240 BC, with estimates of the accuracy of Eratosthenes's measurement ranging from −1% to 15%.
The Earth is only approximately spherical, so no single value serves as its natural radius. Distances from points on the surface to the center range from to . Several different ways of modeling the Earth as a sphere each yield a mean radius of . Regardless of the model, any radius falls between the polar minimum of about and the equatorial maximum of about . The difference correspond to the polar radius being approximately 0.3% shorter than the equatorial radius.
Ellipsoid of revolution
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
and Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
, the Earth is flattened at the poles and bulged at the equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
. Thus, geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
represents the figure of the Earth as an oblate spheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with t ...
. The oblate spheroid, or oblate ellipsoid, is an ellipsoid of revolution obtained by rotating an ellipse about its shorter axis. It is the regular geometric shape that most nearly approximates the shape of the Earth. A spheroid describing the figure of the Earth or other celestial body
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists within the observable universe. In astronomy, the terms ''object'' and ''body'' are of ...
is called a reference ellipsoid. The reference ellipsoid for Earth is called an ''Earth ellipsoid''.
An ellipsoid of revolution is uniquely defined by two quantities. Several conventions for expressing the two quantities are used in geodesy, but they are all equivalent to and convertible with each other:
* Equatorial radius (called ''semimajor axis''), and polar radius (called ''semiminor axis'');
* and eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
;
* and flattening .
Eccentricity and flattening are different ways of expressing how squashed the ellipsoid is. When flattening appears as one of the defining quantities in geodesy, generally it is expressed by its reciprocal. For example, in the WGS 84 spheroid used by today's GPS systems, the reciprocal of the flattening is set to be exactly .
The difference between a sphere and a reference ellipsoid for Earth is small, only about one part in 300. Historically, flattening was computed from grade measurements. Nowadays, geodetic networks and satellite geodesy are used. In practice, many reference ellipsoids have been developed over the centuries from different surveys. The flattening value varies slightly from one reference ellipsoid to another, reflecting local conditions and whether the reference ellipsoid is intended to model the entire Earth or only some portion of it.
A sphere has a single radius of curvature, which is simply the radius of the sphere. More complex surfaces have radii of curvature that vary over the surface. The radius of curvature describes the radius of the sphere that best approximates the surface at that point. Oblate ellipsoids have a constant radius of curvature east to west along parallels, if a graticule is drawn on the surface, but varying curvature in any other direction. For an oblate ellipsoid, the polar radius of curvature is larger than the equatorial
:
because the pole is flattened: the flatter the surface, the larger the sphere must be to approximate it. Conversely, the ellipsoid's north–south radius of curvature at the equator is smaller than the polar
:
where is the distance from the center of the ellipsoid to the equator (semi-major axis), and is the distance from the center to the pole. (semi-minor axis)
Non-spheroidal deviations
Triaxiality (equatorial eccentricity)
The possibility that the Earth's equator is better characterized as an ellipse rather than a circle and therefore that the ellipsoid is triaxial has been a matter of scientific inquiry for many years. Modern technological developments have furnished new and rapid methods for data collection and, since the launch of Sputnik 1, orbital data have been used to investigate the theory of ellipticity. More recent results indicate a 70 m difference between the two equatorial major and minor axes of inertia, with the larger semidiameter pointing to 15° W longitude (and also 180-degree away).Egg or pear shape
Following work by Picard, Italian polymathGiovanni Domenico Cassini
Giovanni Domenico Cassini (8 June 1625 – 14 September 1712) was an Italian-French mathematician, astronomer, astrologer and engineer. Cassini was born in Perinaldo, near Imperia, at that time in the County of Nice, part of the Savoyard sta ...
found that the length of a degree was apparently shorter north of Paris than to the south, implying the Earth to be egg-shaped. In 1498, Christopher Columbus dubiously suggested that the Earth was pear-shaped based on his disparate mobile readings of the angle of the North Star, which he incorrectly interpreted as having varying diurnal motion.
The theory of a slightly pear-shaped Earth arose when data was received from the U.S.'s artificial satellite Vanguard 1 in 1958. It was found to vary in its long periodic orbit, with the Southern Hemisphere exhibiting higher gravitational attraction than the Northern Hemisphere. This indicated a flattening at the South Pole
The South Pole, also known as the Geographic South Pole or Terrestrial South Pole, is the point in the Southern Hemisphere where the Earth's rotation, Earth's axis of rotation meets its surface. It is called the True South Pole to distinguish ...
and a bulge of the same degree at the North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's rotation, Earth's axis of rotation meets its surface. It is called the True North Pole to distingu ...
, with the sea level
Mean sea level (MSL, often shortened to sea level) is an mean, average surface level of one or more among Earth's coastal Body of water, bodies of water from which heights such as elevation may be measured. The global MSL is a type of vertical ...
increased about at the latter. This theory implies the northern middle latitudes to be slightly flattened and the southern middle latitudes correspondingly bulged. Potential factors involved in this aberration include tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the Moon (and to a much lesser extent, the Sun) and are also caused by the Earth and Moon orbiting one another.
Tide tables ...
s and subcrustal motion (e.g. plate tectonics
Plate tectonics (, ) is the scientific theory that the Earth's lithosphere comprises a number of large tectonic plates, which have been slowly moving since 3–4 billion years ago. The model builds on the concept of , an idea developed durin ...
).
John A. O'Keefe and co-authors are credited with the discovery that the Earth had a significant third degree zonal spherical harmonic in its gravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
using Vanguard 1 satellite data. Based on further satellite geodesy data, Desmond King-Hele refined the estimate to a difference between north and south polar radii, owing to a "stem" rising in the North Pole and a depression in the South Pole. The polar asymmetry is about a thousand times smaller than the Earth's flattening and even smaller than its geoidal undulation in some regions.
Geoid
 Modern geodesy tends to retain the ellipsoid of revolution as a reference ellipsoid and treat triaxiality and pear shape as a part of the geoid figure: they are represented by the spherical harmonic coefficients and , respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.
It was stated earlier that measurements are made on the apparent or topographic surface of the Earth and it has just been explained that computations are performed on an ellipsoid. One other surface is involved in geodetic measurement: the geoid. In geodetic surveying, the computation of the geodetic coordinates of points is commonly performed on a reference ellipsoid closely approximating the size and shape of the Earth in the area of the survey. The actual measurements made on the surface of the Earth with certain instruments are however referred to the geoid. The ellipsoid is a mathematically defined regular surface with specific dimensions. The geoid, on the other hand, coincides with that surface to which the oceans would conform over the entire Earth if free to adjust to the combined effect of the Earth's mass attraction (
Modern geodesy tends to retain the ellipsoid of revolution as a reference ellipsoid and treat triaxiality and pear shape as a part of the geoid figure: they are represented by the spherical harmonic coefficients and , respectively, corresponding to degree and order numbers 2.2 for the triaxiality and 3.0 for the pear shape.
It was stated earlier that measurements are made on the apparent or topographic surface of the Earth and it has just been explained that computations are performed on an ellipsoid. One other surface is involved in geodetic measurement: the geoid. In geodetic surveying, the computation of the geodetic coordinates of points is commonly performed on a reference ellipsoid closely approximating the size and shape of the Earth in the area of the survey. The actual measurements made on the surface of the Earth with certain instruments are however referred to the geoid. The ellipsoid is a mathematically defined regular surface with specific dimensions. The geoid, on the other hand, coincides with that surface to which the oceans would conform over the entire Earth if free to adjust to the combined effect of the Earth's mass attraction (gravitation
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
) and the centrifugal force of the Earth's rotation
Earth's rotation or Earth's spin is the rotation of planet Earth around its own Rotation around a fixed axis, axis, as well as changes in the orientation (geometry), orientation of the rotation axis in space. Earth rotates eastward, in progra ...
. As a result of the uneven distribution of the Earth's mass, the geoidal surface is irregular and, since the ellipsoid is a regular surface, the separations between the two, referred to as geoid undulations, geoid heights, or geoid separations, will be irregular as well.
The geoid is a surface along which the gravity potential is equal everywhere and to which the direction of gravity is always perpendicular. The latter is particularly important because optical instruments containing gravity-reference leveling devices are commonly used to make geodetic measurements. When properly adjusted, the vertical axis of the instrument coincides with the direction of gravity and is, therefore, perpendicular to the geoid. The angle between the plumb line which is perpendicular to the geoid (sometimes called "the vertical") and the perpendicular to the ellipsoid (sometimes called "the ellipsoidal normal") is defined as the deflection of the vertical. It has two components: an east–west and a north–south component.
Local approximations
Simpler local approximations are possible.Local tangent plane
Osculating sphere
refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
measurements and in some navigation and surveillance applications.
Earth rotation and Earth's interior
Determining the exact figure of the Earth is not only a geometric task of geodesy, but also has geophysical considerations. According to theoretical arguments by Newton,Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
, and others, a body having a uniform density of 5,515 kg/m that rotates like the Earth should have a flattening of 1:229. This can be concluded without any information about the composition of Earth's interior.
However, the measured flattening is 1:298.25, which is closer to a sphere and a strong argument that Earth's core is extremely compact. Therefore, the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
must be a function of the depth, ranging from 2,600 kg/m at the surface (rock density of granite
Granite ( ) is a coarse-grained (phanerite, phaneritic) intrusive rock, intrusive igneous rock composed mostly of quartz, alkali feldspar, and plagioclase. It forms from magma with a high content of silica and alkali metal oxides that slowly coo ...
, etc.), up to 13,000 kg/m within the inner core.
Global and regional gravity field
Also with implications for the physical exploration of the Earth's interior is thegravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
, which is the net effect of gravitation (due to mass attraction) and centrifugal force (due to rotation). It can be measured very accurately at the surface and remotely by satellites. True vertical generally does not correspond to theoretical vertical ( deflection ranges up to 50") because topography
Topography is the study of the forms and features of land surfaces. The topography of an area may refer to the landforms and features themselves, or a description or depiction in maps.
Topography is a field of geoscience and planetary sci ...
and all ''geological masses'' disturb the gravitational field. Therefore, the gross structure of the Earth's crust
Earth's crust is its thick outer shell of rock, referring to less than one percent of the planet's radius and volume. It is the top component of the lithosphere, a solidified division of Earth's layers that includes the crust and the upper ...
and mantle can be determined by geodetic-geophysical models of the subsurface.
See also
* Clairaut's theorem * EGM96 * Gravity formula * *Meridian arc
In geodesy and navigation, a meridian arc is the curve (geometry), curve between two points near the Earth's surface having the same longitude. The term may refer either to a arc (geometry), segment of the meridian (geography), meridian, or to its ...
; History:
* Pierre Bouguer
* Earth's circumference#History
* Earth's radius#History
* Flat Earth
* Friedrich Robert Helmert
* History of geodesy
* History of the metre
* Meridian arc#History
* Seconds pendulum
References
;AttributionFurther reading
* Guy Bomford, ''Geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
'', Oxford 1952 and 1980.
* Guy Bomford, ''Determination of the European geoid by means of vertical deflections''. Rpt of Comm. 14, IUGG 10th Gen. Ass., Rome 1954.
* Karl Ledersteger and Gottfried Gerstbach, ''Die horizontale Isostasie / Das isostatische Geoid 31. Ordnung''. Geowissenschaftliche Mitteilungen Band 5, TU Wien 1975.
* Helmut Moritz and Bernhard Hofmann, ''Physical Geodesy''. Springer
Springer or springers may refer to:
Publishers
* Springer Science+Business Media, aka Springer International Publishing, a worldwide publishing group founded in 1842 in Germany formerly known as Springer-Verlag.
** Springer Nature, a multinationa ...
, Wien & New York 2005.
* ''Geodesy for the Layman'', Defense Mapping Agency, St. Louis, 1983.
External links
Reference Ellipsoids (PCI Geomatics)
Jos Leys "The shape of Planet Earth"
{{Authority control Earth Geodesy Geophysics