Dulong–Petit Law on:
[Wikipedia]
[Google]
[Amazon]
 The Dulong–Petit law, a thermodynamic law proposed by French physicists
The Dulong–Petit law, a thermodynamic law proposed by French physicists
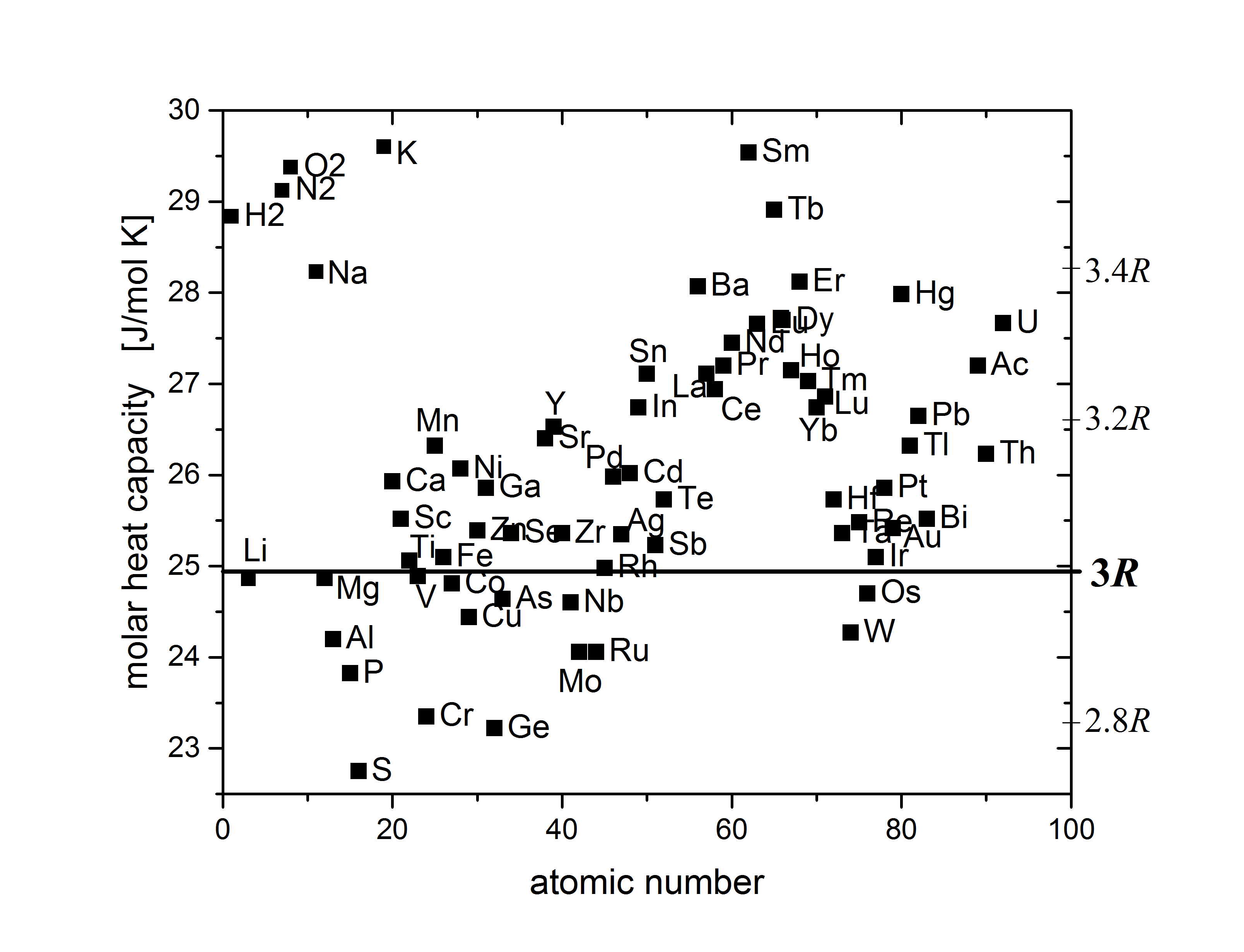
 Despite its simplicity, Dulong–Petit law offers a fairly good prediction for the heat capacity of many elementary solids with relatively simple crystal structure at high
Despite its simplicity, Dulong–Petit law offers a fairly good prediction for the heat capacity of many elementary solids with relatively simple crystal structure at high
 The Dulong–Petit law, a thermodynamic law proposed by French physicists
The Dulong–Petit law, a thermodynamic law proposed by French physicists Pierre Louis Dulong
Pierre Louis Dulong FRS FRSE (; ; 12 February 1785 – 19 July 1838) was a French physicist and chemist. He is remembered today largely for the law of Dulong and Petit, although he was much-lauded by his contemporaries for his studies into ...
and Alexis Thérèse Petit
Alexis Thérèse Petit (; 2 October 1791 – 21 June 1820) was a French physicist.
Petit is known for his work on the efficiencies of air- and steam-engines, published in 1818 (''Mémoire sur l’emploi du principe des forces vives dans le calcu ...
, states that the classical expression for the molar specific heat capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat ...
of certain chemical elements is constant for temperatures far from the absolute zero
Absolute zero is the lowest possible temperature, a state at which a system's internal energy, and in ideal cases entropy, reach their minimum values. The absolute zero is defined as 0 K on the Kelvin scale, equivalent to −273.15 ° ...
.
In modern terms, Dulong and Petit found that the heat capacity of a mole of many solid elements is about 3''R'', where ''R'' is the universal gas constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment p ...
. The modern theory of the heat capacity of solids states that it is due to lattice vibration
A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. In the context of optically trapped objects, the quantized vibration mode can be defined ...
s in the solid.
History
ExperimentallyPierre Louis Dulong
Pierre Louis Dulong FRS FRSE (; ; 12 February 1785 – 19 July 1838) was a French physicist and chemist. He is remembered today largely for the law of Dulong and Petit, although he was much-lauded by his contemporaries for his studies into ...
and Alexis Thérèse Petit
Alexis Thérèse Petit (; 2 October 1791 – 21 June 1820) was a French physicist.
Petit is known for his work on the efficiencies of air- and steam-engines, published in 1818 (''Mémoire sur l’emploi du principe des forces vives dans le calcu ...
had found in 1819 that the heat capacity per weight (the mass-specific heat capacity) for 13 measured elements was close to a constant value, after it had been multiplied by a number representing the presumed relative atomic weight of the element. These atomic weight
Relative atomic mass (symbol: ''A''; sometimes abbreviated RAM or r.a.m.), also known by the deprecated synonym atomic weight, is a dimensionless physical quantity defined as the ratio of the average mass of atoms of a chemical element in a giv ...
s had shortly before been suggested by John Dalton
John Dalton (; 5 or 6 September 1766 – 27 July 1844) was an English chemist, physicist and meteorologist. He introduced the atomic theory into chemistry. He also researched Color blindness, colour blindness; as a result, the umbrella term ...
and modified by Jacob Berzelius.
Dulong and Petit were unaware of the relationship with ''R'', since this constant had not yet been defined from the later kinetic theory of gases. The value of 3''R'' is about 25 joule
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work d ...
s per kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
, and Dulong and Petit essentially found that this was the heat capacity of certain solid elements per mole of atoms they contained.
The Kopp's law
Kopp's law can refer to either of two relationships discovered by the German chemist Hermann Franz Moritz Kopp (1817–1892).
#Kopp found "that the molecular heat capacity of a solid compound is the sum of the atomic heat capacities of the elemen ...
developed in 1865 by Hermann Franz Moritz Kopp extended the Dulong–Petit law to chemical compounds from further experimental data.
Amedeo Avogadro
Lorenzo Romano Amedeo Carlo Avogadro, Count of Quaregna and Cerreto (, also , ; 9 August 17769 July 1856) was an Italian scientist, most noted for his contribution to molecular theory now known as Avogadro's law, which states that equal volu ...
remarked in 1833 that the law did not fit the experimental data of carbon samples. In 1876, Heinrich Friedrich Weber
Heinrich Friedrich Weber (; ; 7 November 1843 – 24 May 1912) was a physicist born in the town of Magdala, near Weimar.
Biography
Around 1861 he entered the University of Jena, where Ernst Abbe became the first of two physicists who decisi ...
, noticed that the specific heat of diamond was sensible to temperature.
In 1877, Ludwig Boltzmann
Ludwig Eduard Boltzmann ( ; ; 20 February 1844 – 5 September 1906) was an Austrian mathematician and Theoretical physics, theoretical physicist. His greatest achievements were the development of statistical mechanics and the statistical ex ...
showed that the constant value of Dulong–Petit law could be explained in terms of independent classical harmonic oscillators. With the advent of quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
, this assumption was refined by Weber's student, Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
in 1907, employing quantum harmonic oscillators to explain the experimentally observed decrease of the heat capacity at low temperatures in diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of e ...
.
Peter Debye
Peter Joseph William Debye ( ; born Petrus Josephus Wilhelmus Debije, ; March 24, 1884 – November 2, 1966) was a Dutch-American physicist and physical chemist, and Nobel laureate in Chemistry.
Biography
Early life
Born in Maastricht, Neth ...
followed in 1912 with a new model based on Max Planck
Max Karl Ernst Ludwig Planck (; ; 23 April 1858 – 4 October 1947) was a German Theoretical physics, theoretical physicist whose discovery of energy quantum, quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial con ...
's photon gas In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon – including pressure, temperature, and entropy. The most common example of a photon gas in equilibrium ...
, where the vibrations are not to individual oscillators but as vibrational modes of the ionic lattice. Debye's model allowed to predict the behavior of the ionic heat capacity at temperature close to 0 kelvin
The kelvin (symbol: K) is the base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By de ...
, and as the Einstein solid
The Einstein solid is a model of a crystalline solid that contains a large number of independent three-dimensional quantum harmonic oscillators of the same frequency. The independence assumption is relaxed in the Debye model.
While the model pro ...
, both recover the Dulong–Petit law at high temperature.
The electronic heat capacity was overestimated by the 1900 Drude-Lorentz model to be half of the value predicted by Dulong–Petit. With the development of the quantum mechanical free electron model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quan ...
in 1927 by Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld (; 5 December 1868 – 26 April 1951) was a German Theoretical physics, theoretical physicist who pioneered developments in Atomic physics, atomic and Quantum mechanics, quantum physics, and also educated and ...
the electronic contribution was found to be orders of magnitude smaller. This model explained why conductors and insulators have roughly the same heat capacity at large temperatures as it depends mostly on the lattice and not on the electronic properties.
Equivalent forms of statement of the law
An equivalent statement of the Dulong–Petit law in modern terms is that, regardless of the nature of the substance, thespecific heat capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. It is also referred to as massic heat ...
''c'' of a solid element (measured in joule per kelvin per kilogram) is equal to 3''R''/''M'', where ''R'' is the gas constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment p ...
(measured in joule per kelvin per mole) and ''M'' is the molar mass
In chemistry, the molar mass () (sometimes called molecular weight or formula weight, but see related quantities for usage) of a chemical substance ( element or compound) is defined as the ratio between the mass () and the amount of substance ...
(measured in kilogram per mole). Thus, the heat capacity per mole of many elements is 3''R''.
The initial form of the Dulong–Petit law was:
:
where ''K'' is a constant which we know today is about 3''R''.
In modern terms the mass ''m'' of the sample divided by molar mass ''M'' gives the number of moles ''n''.
:
Therefore, using uppercase ''C'' for the full heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
(in joule per kelvin), we have:
:
or
:.
Therefore, the heat capacity of most solid crystalline substances is 3''R'' per mole of substance.
Dulong and Petit did not state their law in terms of the gas constant ''R'' (which was not then known). Instead, they measured the values of heat capacities (per weight) of substances and found them smaller for substances of greater atomic weight as inferred by Dalton and other early atomists. Dulong and Petit then found that when multiplied by these atomic weights, the value for the heat capacity per mole was nearly constant, and equal to a value which was later recognized to be 3''R''.
In other modern terminology, the dimensionless heat capacity ''C''/(n''R'') is equal to 3.
The law can also be written as a function of the total number of atoms ''N'' in the sample:
:,
where ''k''B is Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
.
Application limits
 Despite its simplicity, Dulong–Petit law offers a fairly good prediction for the heat capacity of many elementary solids with relatively simple crystal structure at high
Despite its simplicity, Dulong–Petit law offers a fairly good prediction for the heat capacity of many elementary solids with relatively simple crystal structure at high temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
s. This agreement is because in the classical statistical theory of Ludwig Boltzmann
Ludwig Eduard Boltzmann ( ; ; 20 February 1844 – 5 September 1906) was an Austrian mathematician and Theoretical physics, theoretical physicist. His greatest achievements were the development of statistical mechanics and the statistical ex ...
, the heat capacity of solids approaches a maximum of 3''R'' per mole of atoms because full vibrational-mode degrees of freedom amount to 3 degrees of freedom per atom, each corresponding to a quadratic kinetic energy term and a quadratic potential energy term. By the equipartition theorem
In classical physics, classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energy, energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, ...
, the average of each quadratic term is ''k''B''T'', or ''RT'' per mole (see derivation below). Multiplied by 3 degrees of freedom and the two terms per degree of freedom, this amounts to 3''R'' per mole heat capacity.
The Dulong–Petit law fails at room temperatures for light atoms bonded strongly to each other, such as in metallic beryllium and in carbon as diamond. Here, it predicts higher heat capacities than are actually found, with the difference due to higher-energy vibrational modes not being populated at room temperatures in these substances.
In the very low (cryogenic) temperature region, where the quantum mechanical nature of energy storage in all solids manifests itself with larger and larger effect, the law fails for all substances. For crystals under such conditions, the Debye model
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat ( heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) a ...
, an extension of the Einstein theory that accounts for statistical distributions in atomic vibration when there are lower amounts of energy to distribute, works well.
Derivation for an Einstein solid
A system of vibrations in a crystalline solid lattice can be modeled as an Einstein solid, i.e. by considering ''N''quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, ...
potentials along each degree of freedom. Then, the free energy of the system can be written as
:
where the index ''α'' sums over all the degrees of freedom. In the 1907 Einstein model (as opposed to the later Debye model
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat ( heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) a ...
) we consider only the high-energy limit:
:
Then
:
and we have
:
Define ''geometric mean frequency'' by
:
where ''g'' measures the total number of spatial degrees of freedom of the system.
Thus we have
:
Using energy
:
we have
:
This gives heat capacity at constant volume
:
which is independent of the temperature.
For another more precise derivation, see Debye model
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat ( heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) a ...
.
See also
*Heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity is a ...
* Kopp–Neumann law
References
{{DEFAULTSORT:Dulong-Petit law Condensed matter physics Laws of thermodynamics Statistical mechanics Analytical chemistry