discriminant analysis on:
[Wikipedia]
[Google]
[Amazon]
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in
"Discriminant correspondence analysis."
In: N.J. Salkind (Ed.): ''Encyclopedia of Measurement and Statistic''. Thousand Oaks (CA): Sage. pp. 270–275. Discriminant analysis is used when groups are known a priori (unlike in
Discriminant function analysis: Concept and application
Egitim Arastirmalari - Eurasian Journal of Educational Research, 33, 73-92. In simple terms, discriminant function analysis is classification - the act of distributing things into groups, classes or categories of the same type.
Applied Multivariate Statistical Analysis
'. Springer Berlin Heidelberg. pp. 289-303. *Bayes Discriminant Rule: Assigns to the group that maximizes , where ''πi'' represents the
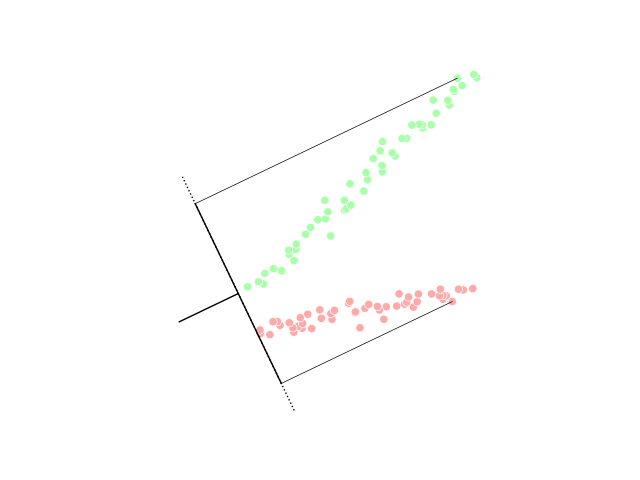 Be sure to note that the vector is the normal to the discriminant
Be sure to note that the vector is the normal to the discriminant

 In the case where there are more than two classes, the analysis used in the derivation of the Fisher discriminant can be extended to find a subspace which appears to contain all of the class variability.Garson, G. D. (2008). Discriminant function analysis. . This generalization is due to C. R. Rao. Suppose that each of C classes has a mean and the same covariance . Then the scatter between class variability may be defined by the sample covariance of the class means
:
where is the mean of the class means. The class separation in a direction in this case will be given by
:
This means that when is an
In the case where there are more than two classes, the analysis used in the derivation of the Fisher discriminant can be extended to find a subspace which appears to contain all of the class variability.Garson, G. D. (2008). Discriminant function analysis. . This generalization is due to C. R. Rao. Suppose that each of C classes has a mean and the same covariance . Then the scatter between class variability may be defined by the sample covariance of the class means
:
where is the mean of the class means. The class separation in a direction in this case will be given by
:
This means that when is an
Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures
Geom. Funct. Anal. 21 (5), 1043–1068.) and for product measures on a multidimensional cube (this is proven using Talagrand's concentration inequality for product probability spaces). Data separability by classical linear discriminants simplifies the problem of error correction for
Discriminant Correlation Analysis (DCA) of the Haghighat article (see above)
ALGLIB
contains open-source LDA implementation in C# / C++ / Pascal / VBA.
LDA in Python
LDA implementation in Python
*
* ttp://people.revoledu.com/kardi/tutorial/LDA/ Discriminant analysis tutorial in Microsoft Excel by Kardi Teknomo
Course notes, Discriminant function analysis by David W. Stockburger, Missouri State University
Discriminant function analysis (DA) by John Poulsen and Aaron French, San Francisco State University
{{DEFAULTSORT:Linear Discriminant Analysis Classification algorithms Market research Market segmentation Statistical classification
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
and other fields, to find a linear combination
In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' a ...
of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier
In machine learning, a linear classifier makes a classification decision for each object based on a linear combination of its features. Such classifiers work well for practical problems such as document classification, and more generally for prob ...
, or, more commonly, for dimensionality reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally ...
before later classification
Classification is the activity of assigning objects to some pre-existing classes or categories. This is distinct from the task of establishing the classes themselves (for example through cluster analysis). Examples include diagnostic tests, identif ...
.
LDA is closely related to analysis of variance
Analysis of variance (ANOVA) is a family of statistical methods used to compare the Mean, means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variati ...
(ANOVA) and regression analysis, which also attempt to express one dependent variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical functio ...
as a linear combination of other features or measurements.
However, ANOVA uses categorical independent variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function ...
and a continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
dependent variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical functio ...
, whereas discriminant analysis has continuous independent variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function ...
and a categorical dependent variable (''i.e.'' the class label). Logistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
and probit regression
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to e ...
are more similar to LDA than ANOVA is, as they also explain a categorical variable by the values of continuous independent variables. These other methods are preferable in applications where it is not reasonable to assume that the independent variables are normally distributed, which is a fundamental assumption of the LDA method.
LDA is also closely related to principal component analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
The data is linearly transformed onto a new coordinate system such that th ...
(PCA) and factor analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observe ...
in that they both look for linear combinations of variables which best explain the data. LDA explicitly attempts to model the difference between the classes of data. PCA, in contrast, does not take into account any difference in class, and factor analysis builds the feature combinations based on differences rather than similarities. Discriminant analysis is also different from factor analysis in that it is not an interdependence technique: a distinction between independent variables and dependent variables (also called criterion variables) must be made.
LDA works when the measurements made on independent variables for each observation are continuous quantities. When dealing with categorical independent variables, the equivalent technique is discriminant correspondence analysis.Abdi, H. (2007"Discriminant correspondence analysis."
In: N.J. Salkind (Ed.): ''Encyclopedia of Measurement and Statistic''. Thousand Oaks (CA): Sage. pp. 270–275. Discriminant analysis is used when groups are known a priori (unlike in
cluster analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the ...
). Each case must have a score on one or more quantitative predictor measures, and a score on a group measure.Büyüköztürk, Ş. & Çokluk-Bökeoğlu, Ö. (2008)Discriminant function analysis: Concept and application
Egitim Arastirmalari - Eurasian Journal of Educational Research, 33, 73-92. In simple terms, discriminant function analysis is classification - the act of distributing things into groups, classes or categories of the same type.
History
The originaldichotomous
A dichotomy () is a partition of a set, partition of a whole (or a set) into two parts (subsets). In other words, this couple of parts must be
* jointly exhaustive: everything must belong to one part or the other, and
* mutually exclusive: nothi ...
discriminant analysis was developed by Sir Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who a ...
in 1936.Cohen et al. Applied Multiple Regression/Correlation Analysis for the Behavioural Sciences 3rd ed. (2003). Taylor & Francis Group. It is different from an ANOVA
Analysis of variance (ANOVA) is a family of statistical methods used to compare the means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''w ...
or MANOVA
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests ...
, which is used to predict one (ANOVA) or multiple (MANOVA) continuous dependent variables by one or more independent categorical variables. Discriminant function analysis is useful in determining whether a set of variables is effective in predicting category membership.
LDA for two classes
Consider a set of observations (also called features, attributes, variables or measurements) for each sample of an object or event with known class . This set of samples is called thetraining set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from ...
in a supervised learning
In machine learning, supervised learning (SL) is a paradigm where a Statistical model, model is trained using input objects (e.g. a vector of predictor variables) and desired output values (also known as a ''supervisory signal''), which are often ...
context. The classification problem is then to find a good predictor for the class of any sample of the same distribution (not necessarily from the training set) given only an observation .
LDA approaches the problem by assuming that the conditional probability density function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
s and are both the normal distribution
''The'' is a grammatical article in English, denoting nouns that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The ...
with mean and covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.
The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one ...
parameters and , respectively. Under this assumption, the Bayes-optimal solution is to predict points as being from the second class if the log of the likelihood ratios is bigger than some threshold T, so that:
:
Without any further assumptions, the resulting classifier is referred to as quadratic discriminant analysis (QDA).
LDA instead makes the additional simplifying homoscedasticity assumption (''i.e.'' that the class covariances are identical, so ) and that the covariances have full rank.
In this case, several terms cancel:
:
: because is Hermitian {{Short description, none
Numerous things are named after the French mathematician Charles Hermite (1822–1901):
Hermite
* Cubic Hermite spline, a type of third-degree spline
* Gauss–Hermite quadrature, an extension of Gaussian quadrature me ...
and the above decision criterion
becomes a threshold on the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
:
for some threshold constant ''c'', where
:
:
This means that the criterion of an input being in a class is purely a function of this linear combination of the known observations.
It is often useful to see this conclusion in geometrical terms: the criterion of an input being in a class is purely a function of projection of multidimensional-space point onto vector (thus, we only consider its direction). In other words, the observation belongs to if corresponding is located on a certain side of a hyperplane perpendicular to . The location of the plane is defined by the threshold .
Assumptions
The assumptions of discriminant analysis are the same as those for MANOVA. The analysis is quite sensitive to outliers and the size of the smallest group must be larger than the number of predictor variables. * Multivariate normality: Independent variables are normal for each level of the grouping variable. *Homogeneity of variance/covariance (homoscedasticity
In statistics, a sequence of random variables is homoscedastic () if all its random variables have the same finite variance; this is also known as homogeneity of variance. The complementary notion is called heteroscedasticity, also known as hete ...
): Variances among group variables are the same across levels of predictors. Can be tested with Box's M statistic. It has been suggested, however, that linear discriminant analysis be used when covariances are equal, and that quadratic discriminant analysis may be used when covariances are not equal.
*Independence
Independence is a condition of a nation, country, or state, in which residents and population, or some portion thereof, exercise self-government, and usually sovereignty, over its territory. The opposite of independence is the status of ...
: Participants are assumed to be randomly sampled, and a participant's score on one variable is assumed to be independent of scores on that variable for all other participants.
It has been suggested that discriminant analysis is relatively robust to slight violations of these assumptions, and it has also been shown that discriminant analysis may still be reliable when using dichotomous variables (where multivariate normality is often violated).
Discriminant functions
Discriminant analysis works by creating one or more linear combinations of predictors, creating a newlatent variable
In statistics, latent variables (from Latin: present participle of ) are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or measured. Such '' latent va ...
for each function. These functions are called discriminant functions. The number of functions possible is either where = number of groups, or (the number of predictors), whichever is smaller. The first function created maximizes the differences between groups on that function. The second function maximizes differences on that function, but also must not be correlated with the previous function. This continues with subsequent functions with the requirement that the new function not be correlated with any of the previous functions.
Given group , with sets of sample space, there is a discriminant rule such that if , then . Discriminant analysis then, finds “good” regions of to minimize classification error, therefore leading to a high percent correct classified in the classification table.
Each function is given a discriminant score to determine how well it predicts group placement.
*Structure Correlation Coefficients: The correlation between each predictor and the discriminant score of each function. This is a zero-order correlation (i.e., not corrected for the other predictors).
*Standardized Coefficients: Each predictor's weight in the linear combination that is the discriminant function. Like in a regression equation, these coefficients are partial (i.e., corrected for the other predictors). Indicates the unique contribution of each predictor in predicting group assignment.
*Functions at Group Centroids: Mean discriminant scores for each grouping variable are given for each function. The farther apart the means are, the less error there will be in classification.
Discrimination rules
*Maximum likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
: Assigns to the group that maximizes population (group) density.Hardle, W., Simar, L. (2007). Applied Multivariate Statistical Analysis
'. Springer Berlin Heidelberg. pp. 289-303. *Bayes Discriminant Rule: Assigns to the group that maximizes , where ''πi'' represents the
prior probability
A prior probability distribution of an uncertain quantity, simply called the prior, is its assumed probability distribution before some evidence is taken into account. For example, the prior could be the probability distribution representing the ...
of that classification, and represents the population density.
* Fisher's linear discriminant rule: Maximizes the ratio between ''SS''between and ''SS''within, and finds a linear combination of the predictors to predict group.
Eigenvalues
Aneigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
in discriminant analysis is the characteristic root of each function. It is an indication of how well that function differentiates the groups, where the larger the eigenvalue, the better the function differentiates. This however, should be interpreted with caution, as eigenvalues have no upper limit.
The eigenvalue can be viewed as a ratio of ''SS''between and ''SS''within as in ANOVA when the dependent variable is the discriminant function, and the groups are the levels of the IV. This means that the largest eigenvalue is associated with the first function, the second largest with the second, etc..
Effect size
Some suggest the use of eigenvalues aseffect size
In statistics, an effect size is a value measuring the strength of the relationship between two variables in a population, or a sample-based estimate of that quantity. It can refer to the value of a statistic calculated from a sample of data, the ...
measures, however, this is generally not supported. Instead, the canonical correlation
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X'n'') and ''Y'' ...
is the preferred measure of effect size. It is similar to the eigenvalue, but is the square root of the ratio of ''SS''between and ''SS''total. It is the correlation between groups and the function.
Another popular measure of effect size is the percent of variance for each function. This is calculated by: (''λx/Σλi'') X 100 where ''λx'' is the eigenvalue for the function and Σ''λi'' is the sum of all eigenvalues. This tells us how strong the prediction is for that particular function compared to the others.
Percent correctly classified can also be analyzed as an effect size. The kappa value can describe this while correcting for chance agreement.
Canonical discriminant analysis for ''k'' classes
Canonical discriminant analysis (CDA) finds axes (''k'' − 1canonical coordinates
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of cla ...
, ''k'' being the number of classes) that best separate the categories. These linear functions are uncorrelated and define, in effect, an optimal ''k'' − 1 space through the ''n''-dimensional cloud of data that best separates (the projections in that space of) the ''k'' groups. See “ Multiclass LDA” for details below.
Because LDA uses canonical variates, it was initially often referred as the "method of canonical variates" or canonical variates analysis (CVA).
Fisher's linear discriminant
The terms ''Fisher's linear discriminant'' and ''LDA'' are often used interchangeably, although Fisher's original article actually describes a slightly different discriminant, which does not make some of the assumptions of LDA such asnormally distributed
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real number, real-valued random variable. The general form of its probability density function is
f(x ...
classes or equal class covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.
The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one ...
s.
Suppose two classes of observations have mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
s and covariances . Then the linear combination of features will have mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
s and variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
s for . Fisher defined the separation between these two distributions to be the ratio of the variance between the classes to the variance within the classes:
:
This measure is, in some sense, a measure of the signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to noise power, often expressed in deci ...
for the class labelling. It can be shown that the maximum separation occurs when
:
When the assumptions of LDA are satisfied, the above equation is equivalent to LDA.
 Be sure to note that the vector is the normal to the discriminant
Be sure to note that the vector is the normal to the discriminant hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
. As an example, in a two dimensional problem, the line that best divides the two groups is perpendicular to .
Generally, the data points to be discriminated are projected onto ; then the threshold that best separates the data is chosen from analysis of the one-dimensional distribution. There is no general rule for the threshold. However, if projections of points from both classes exhibit approximately the same distributions, a good choice would be the hyperplane between projections of the two means, and . In this case the parameter c in threshold condition can be found explicitly:
:.
Otsu's method is related to Fisher's linear discriminant, and was created to binarize the histogram of pixels in a grayscale image
In digital photography, computer-generated imagery, and colorimetry, a greyscale (more common in Commonwealth English) or grayscale (more common in American English) image is one in which the value of each pixel is a single sample (signal), s ...
by optimally picking the black/white threshold that minimizes intra-class variance and maximizes inter-class variance within/between grayscales assigned to black and white pixel classes.
Multiclass LDA

 In the case where there are more than two classes, the analysis used in the derivation of the Fisher discriminant can be extended to find a subspace which appears to contain all of the class variability.Garson, G. D. (2008). Discriminant function analysis. . This generalization is due to C. R. Rao. Suppose that each of C classes has a mean and the same covariance . Then the scatter between class variability may be defined by the sample covariance of the class means
:
where is the mean of the class means. The class separation in a direction in this case will be given by
:
This means that when is an
In the case where there are more than two classes, the analysis used in the derivation of the Fisher discriminant can be extended to find a subspace which appears to contain all of the class variability.Garson, G. D. (2008). Discriminant function analysis. . This generalization is due to C. R. Rao. Suppose that each of C classes has a mean and the same covariance . Then the scatter between class variability may be defined by the sample covariance of the class means
:
where is the mean of the class means. The class separation in a direction in this case will be given by
:
This means that when is an eigenvector
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by ...
of the separation will be equal to the corresponding eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
.
If is diagonalizable, the variability between features will be contained in the subspace spanned by the eigenvectors corresponding to the ''C'' − 1 largest eigenvalues (since is of rank ''C'' − 1 at most). These eigenvectors are primarily used in feature reduction, as in PCA. The eigenvectors corresponding to the smaller eigenvalues will tend to be very sensitive to the exact choice of training data, and it is often necessary to use regularisation as described in the next section.
If classification is required, instead of dimension reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally ...
, there are a number of alternative techniques available. For instance, the classes may be partitioned, and a standard Fisher discriminant or LDA used to classify each partition. A common example of this is "one against the rest" where the points from one class are put in one group, and everything else in the other, and then LDA applied. This will result in C classifiers, whose results are combined. Another common
method is pairwise classification, where a new classifier is created for each pair of classes (giving ''C''(''C'' − 1)/2 classifiers in total), with the individual classifiers combined to produce a final classification.
Incremental LDA
The typical implementation of the LDA technique requires that all the samples are available in advance. However, there are situations where the entire data set is not available and the input data are observed as a stream. In this case, it is desirable for the LDA feature extraction to have the ability to update the computed LDA features by observing the new samples without running the algorithm on the whole data set. For example, in many real-time applications such as mobile robotics or on-line face recognition, it is important to update the extracted LDA features as soon as new observations are available. An LDA feature extraction technique that can update the LDA features by simply observing new samples is an ''incremental LDA algorithm'', and this idea has been extensively studied over the last two decades. Chatterjee and Roychowdhury proposed an incremental self-organized LDA algorithm for updating the LDA features. In other work, Demir and Ozmehmet proposed online local learning algorithms for updating LDA features incrementally using error-correcting and the Hebbian learning rules. Later, Aliyari et al. derived fast incremental algorithms to update the LDA features by observing the new samples.Practical use
In practice, the class means and covariances are not known. They can, however, be estimated from the training set. Either themaximum likelihood estimate
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
or the maximum a posteriori
An estimation procedure that is often claimed to be part of Bayesian statistics is the maximum a posteriori (MAP) estimate of an unknown quantity, that equals the mode of the posterior density with respect to some reference measure, typically ...
estimate may be used in place of the exact value in the above equations. Although the estimates of the covariance may be considered optimal in some sense, this does not mean that the resulting discriminant obtained by substituting these values is optimal in any sense, even if the assumption of normally distributed classes is correct.
Another complication in applying LDA and Fisher's discriminant to real data occurs when the number of measurements of each sample (i.e., the dimensionality of each data vector) exceeds the number of samples in each class. In this case, the covariance estimates do not have full rank, and so cannot be inverted. There are a number of ways to deal with this. One is to use a pseudo inverse instead of the usual matrix inverse in the above formulae. However, better numeric stability may be achieved by first projecting the problem onto the subspace spanned by .
Another strategy to deal with small sample size is to use a shrinkage estimator of the covariance matrix, which
can be expressed mathematically as
:
where is the identity matrix, and is the ''shrinkage intensity'' or ''regularisation parameter''.
This leads to the framework of regularized discriminant analysis or shrinkage discriminant analysis.
Also, in many practical cases linear discriminants are not suitable. LDA and Fisher's discriminant can be extended for use in non-linear classification via the kernel trick
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). These methods involve using linear classifiers to solve nonlinear problems. The general task of pa ...
. Here, the original observations are effectively mapped into a higher dimensional non-linear space. Linear classification in this non-linear space is then equivalent to non-linear classification in the original space. The most commonly used example of this is the kernel Fisher discriminant.
LDA can be generalized to multiple discriminant analysis, where ''c'' becomes a categorical variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or ...
with ''N'' possible states, instead of only two. Analogously, if the class-conditional densities are normal with shared covariances, the sufficient statistic
In statistics, sufficiency is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. A sufficient statistic contains all of the information that the dataset provides about the model parameters. It ...
for are the values of ''N'' projections, which are the subspace spanned by the ''N'' means, affine projected by the inverse covariance matrix. These projections can be found by solving a generalized eigenvalue problem
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the mat ...
, where the numerator is the covariance matrix formed by treating the means as the samples, and the denominator is the shared covariance matrix. See “ Multiclass LDA” above for details.
Applications
In addition to the examples given below, LDA is applied in positioning andproduct management
Product management is the business process of planning, developing, launching, and managing a product or service. It includes the entire lifecycle of a product, from ideation to development to go to market. Product managers are responsible for ...
.
Bankruptcy prediction
In bankruptcy prediction based on accounting ratios and other financial variables, linear discriminant analysis was the first statistical method applied to systematically explain which firms entered bankruptcy vs. survived. Despite limitations including known nonconformance of accounting ratios to the normal distribution assumptions of LDA,Edward Altman
Edward I. Altman (born June 5, 1941) is a Professor of Finance, Emeritus, at New York University's Stern School of Business. He is best known for the development of the Altman Z-score for predicting bankruptcy which he published in 1968. Profe ...
's 1968 model is still a leading model in practical applications.
Face recognition
In computerisedface recognition
A facial recognition system is a technology potentially capable of matching a human face from a digital image or a Film frame, video frame against a database of faces. Such a system is typically employed to authenticate users through ID verif ...
, each face is represented by a large number of pixel values. Linear discriminant analysis is primarily used here to reduce the number of features to a more manageable number before classification. Each of the new dimensions is a linear combination of pixel values, which form a template. The linear combinations obtained using Fisher's linear discriminant are called ''Fisher faces'', while those obtained using the related principal component analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing.
The data is linearly transformed onto a new coordinate system such that th ...
are called '' eigenfaces''.
Marketing
Inmarketing
Marketing is the act of acquiring, satisfying and retaining customers. It is one of the primary components of Business administration, business management and commerce.
Marketing is usually conducted by the seller, typically a retailer or ma ...
, discriminant analysis was once often used to determine the factors which distinguish different types of customers and/or products on the basis of surveys or other forms of collected data. Logistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
or other methods are now more commonly used. The use of discriminant analysis in marketing can be described by the following steps:
#Formulate the problem and gather data—Identify the salient attributes consumers use to evaluate products in this category—Use quantitative marketing research
Quantitative marketing research is the application of quantitative research techniques to the field of marketing research. It has roots in both the positivist view of the world, and the modern marketing viewpoint that marketing is an interactive ...
techniques (such as surveys) to collect data from a sample of potential customers concerning their ratings of all the product attributes. The data collection stage is usually done by marketing research professionals. Survey questions ask the respondent to rate a product from one to five (or 1 to 7, or 1 to 10) on a range of attributes chosen by the researcher. Anywhere from five to twenty attributes are chosen. They could include things like: ease of use, weight, accuracy, durability, colourfulness, price, or size. The attributes chosen will vary depending on the product being studied. The same question is asked about all the products in the study. The data for multiple products is codified and input into a statistical program such as R, SPSS
SPSS Statistics is a statistical software suite developed by IBM for data management, advanced analytics, multivariate analysis, business intelligence, and criminal investigation. Long produced by SPSS Inc., it was acquired by IBM in 2009. Versi ...
or SAS. (This step is the same as in Factor analysis).
#Estimate the Discriminant Function Coefficients and determine the statistical significance and validity—Choose the appropriate discriminant analysis method. The direct method involves estimating the discriminant function so that all the predictors are assessed simultaneously. The stepwise method enters the predictors sequentially. The two-group method should be used when the dependent variable has two categories or states. The multiple discriminant method is used when the dependent variable has three or more categorical states. Use Wilks's Lambda to test for significance in SPSS or F stat in SAS. The most common method used to test validity is to split the sample into an estimation or analysis sample, and a validation or holdout sample. The estimation sample is used in constructing the discriminant function. The validation sample is used to construct a classification matrix which contains the number of correctly classified and incorrectly classified cases. The percentage of correctly classified cases is called the ''hit ratio''.
#Plot the results on a two dimensional map, define the dimensions, and interpret the results. The statistical program (or a related module) will map the results. The map will plot each product (usually in two-dimensional space). The distance of products to each other indicate either how different they are. The dimensions must be labelled by the researcher. This requires subjective judgement and is often very challenging. See perceptual mapping.
Biomedical studies
The main application of discriminant analysis in medicine is the assessment of severity state of a patient and prognosis of disease outcome. For example, during retrospective analysis, patients are divided into groups according to severity of disease – mild, moderate, and severe form. Then results of clinical and laboratory analyses are studied to reveal statistically different variables in these groups. Using these variables, discriminant functions are built to classify disease severity in future patients. Additionally, Linear Discriminant Analysis (LDA) can help select more discriminative samples for data augmentation, improving classification performance. In biology, similar principles are used in order to classify and define groups of different biological objects, for example, to define phage types of Salmonella enteritidis based on Fourier transform infrared spectra, to detect animal source of ''Escherichia coli'' studying its virulence factors etc.Earth science
This method can be used to . For example, when different data from various zones are available, discriminant analysis can find the pattern within the data and classify it effectively.Comparison to logistic regression
Discriminant function analysis is very similar tologistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
, and both can be used to answer the same research questions. Logistic regression does not have as many assumptions and restrictions as discriminant analysis. However, when discriminant analysis’ assumptions are met, it is more powerful than logistic regression. Unlike logistic regression, discriminant analysis can be used with small sample sizes. It has been shown that when sample sizes are equal, and homogeneity of variance/covariance holds, discriminant analysis is more accurate. Despite all these advantages, logistic regression has none-the-less become the common choice, since the assumptions of discriminant analysis are rarely met.
Linear discriminant in high dimensions
Geometric anomalies in higher dimensions lead to the well-knowncurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. T ...
. Nevertheless, proper utilization of concentration of measure phenomena can make computation easier. An important case of these ''blessing of dimensionality'' phenomena was highlighted by Donoho and Tanner: if a sample is essentially high-dimensional then each point can be separated from the rest of the sample by linear inequality, with high probability, even for exponentially large samples. These linear inequalities can be selected in the standard (Fisher's) form of the linear discriminant for a rich family of probability distribution. In particular, such theorems are proven for log-concave distributions including multidimensional normal distribution (the proof is based on the concentration inequalities for log-concave measuresGuédon, O., Milman, E. (2011Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures
Geom. Funct. Anal. 21 (5), 1043–1068.) and for product measures on a multidimensional cube (this is proven using Talagrand's concentration inequality for product probability spaces). Data separability by classical linear discriminants simplifies the problem of error correction for
artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
systems in high dimension.
See also
*Data mining
Data mining is the process of extracting and finding patterns in massive data sets involving methods at the intersection of machine learning, statistics, and database systems. Data mining is an interdisciplinary subfield of computer science and ...
*Decision tree learning
Decision tree learning is a supervised learning approach used in statistics, data mining and machine learning. In this formalism, a classification or regression decision tree is used as a predictive model to draw conclusions about a set of obser ...
*Factor analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observe ...
* Kernel Fisher discriminant analysis
*Logit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in Data transformation (statistics), data transformations.
Ma ...
(for logistic regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regres ...
)
*Linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
* Multiple discriminant analysis
*Multidimensional scaling
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a data set. MDS is used to translate distances between each pair of n objects in a set into a configuration of n points mapped into an ...
*Pattern recognition
Pattern recognition is the task of assigning a class to an observation based on patterns extracted from data. While similar, pattern recognition (PR) is not to be confused with pattern machines (PM) which may possess PR capabilities but their p ...
* Preference regression
*Quadratic classifier
In statistics, a quadratic classifier is a statistical classifier that uses a quadratic decision surface to separate measurements of two or more classes of objects or events. It is a more general version of the linear classifier.
The classific ...
*Statistical classification
When classification is performed by a computer, statistical methods are normally used to develop the algorithm.
Often, the individual observations are analyzed into a set of quantifiable properties, known variously as explanatory variables or ''f ...
References
Further reading
* * * * * *External links
Discriminant Correlation Analysis (DCA) of the Haghighat article (see above)
ALGLIB
contains open-source LDA implementation in C# / C++ / Pascal / VBA.
LDA in Python
LDA implementation in Python
*
* ttp://people.revoledu.com/kardi/tutorial/LDA/ Discriminant analysis tutorial in Microsoft Excel by Kardi Teknomo
Course notes, Discriminant function analysis by David W. Stockburger, Missouri State University
Discriminant function analysis (DA) by John Poulsen and Aaron French, San Francisco State University
{{DEFAULTSORT:Linear Discriminant Analysis Classification algorithms Market research Market segmentation Statistical classification