digonal disphenoid on:
[Wikipedia]
[Google]
[Amazon]
In
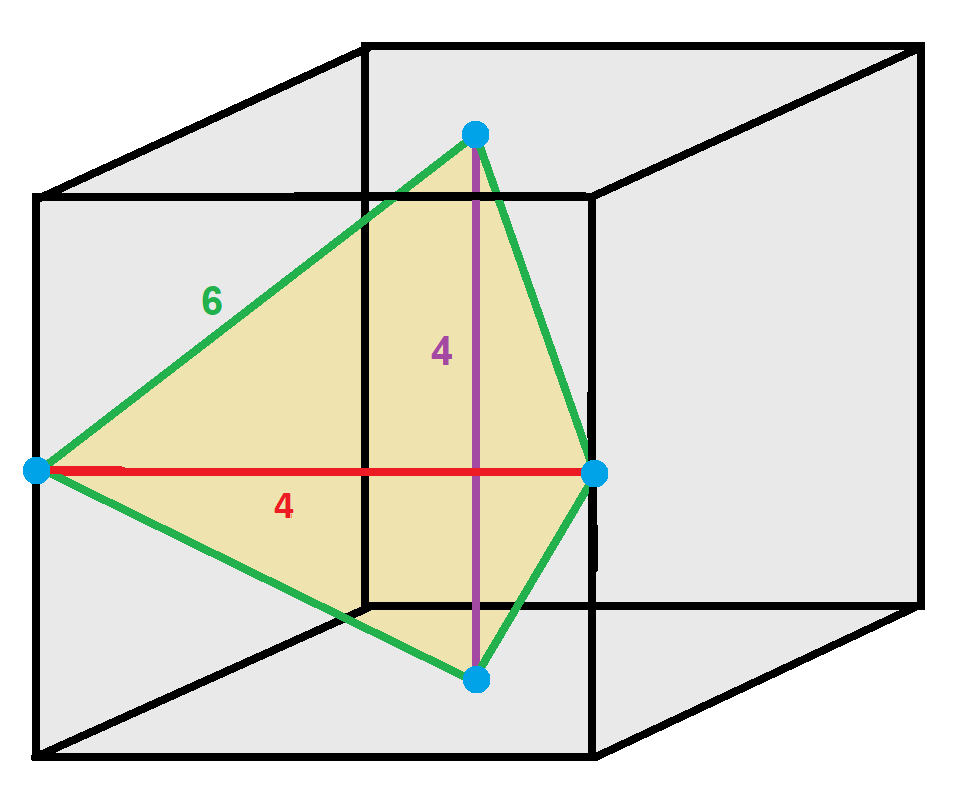 Some tetragonal disphenoids will form
Some tetragonal disphenoids will form
Mathematical Analysis of Disphenoid by H C Rajpoot
from Academia.edu * * {{Mathworld , urlname=IsoscelesTetrahedron , title=Isosceles tetrahedron Tetrahedra
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a disphenoid () is a tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
whose four faces
The face is the front of the head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect the ...
are congruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,. sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron.
All the solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poin ...
s and vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
s of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
s. However, a disphenoid is not a regular polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...
, because, in general, its faces are not regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s, and its edges have three different lengths.
Special cases and generalizations
If the faces of a disphenoid areequilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
s, it is a regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
with Td tetrahedral symmetry
image:tetrahedron.svg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that co ...
, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
s, it is called a tetragonal disphenoid. In this case it has D2d dihedral symmetry
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, g ...
.
A sphenoid with scalene triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional ...
s as its faces is called a rhombic disphenoid and it has D2 dihedral symmetry. Unlike the tetragonal disphenoid, the rhombic disphenoid has no reflection symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a Reflection (mathematics), reflection. That is, a figure which does not change upon undergoing a reflection has reflecti ...
, so it is chiral
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is dist ...
.
Both tetragonal disphenoids and rhombic disphenoids are isohedra: as well as being congruent to each other, all of their faces are symmetric to each other.
It is not possible to construct a disphenoid with right triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees).
The side opposite to the right angle i ...
or obtuse triangle
An acute triangle (or acute-angled triangle) is a triangle with three ''acute angles'' (less than 90°). An obtuse triangle (or obtuse-angled triangle) is a triangle with one '' obtuse angle'' (greater than 90°) and two acute angles. Since a trian ...
faces. When right triangles are glued together in the pattern of a disphenoid, they form a flat figure (a doubly-covered rectangle) that does not enclose any volume.. When obtuse triangles are glued in this way, the resulting surface can be folded to form a disphenoid (by Alexandrov's uniqueness theorem
Alexandrov's theorem on polyhedra is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each othe ...
) but one with acute triangle faces and with edges that in general do not lie along the edges of the given obtuse triangles.
Two more types of tetrahedron generalize the disphenoid and have similar names. The digonal disphenoid has faces with two different shapes, both isosceles triangles, with two faces of each shape. The phyllic disphenoid similarly has faces with two shapes of scalene triangles.
Disphenoids can also be seen as digonal antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
s or as alternated quadrilateral prism
PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...
s.
Characterizations
A tetrahedron is a disphenoidif and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
its circumscribed parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square.
Three equiva ...
is right-angled.
We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's Vertex (geometry), vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the te ...
and the inscribed sphere
image:Circumcentre.svg, An inscribed triangle of a circle
In geometry, an inscribed plane (geometry), planar shape or solid (geometry), solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figu ...
coincide..
Another characterization states that if ''d1'', ''d2'' and ''d3'' are the common perpendiculars of ''AB'' and ''CD''; ''AC'' and ''BD''; and ''AD'' and ''BC'' respectively in a tetrahedron ''ABCD'', then the tetrahedron is a disphenoid if and only if ''d1'', ''d2'' and ''d3'' are pairwise perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
..
The disphenoids are the only polyhedra having infinitely many non-self-intersecting closed geodesic In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold is a geodesic that returns to its starting point with the same tangent direction. It may be formalized as the projection of a closed orbit of the geodesic f ...
s. On a disphenoid, all closed geodesics are non-self-intersecting.
The disphenoids are the tetrahedra in which all four faces have the same perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
, the tetrahedra in which all four faces have the same area, and the tetrahedra in which the angular defect In geometry, the angular defect or simply defect (also called deficit or deficiency) is the failure of some angles to add up to the expected amount of 360° or 180°, when such angles in the Euclidean plane would. The opposite notion is the ''exces ...
s of all four vertices equal . They are the polyhedra having a net in the shape of an acute triangle, divided into four similar triangles
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly ...
by segments connecting the edge midpoints..
Metric formulas
Thevolume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch) ...
of a disphenoid with opposite edges of length ''l'', ''m'' and ''n'' is given by.
:
The circumscribed sphere
In geometry, a circumscribed sphere of a polyhedron is a sphere that contains the polyhedron and touches each of the polyhedron's Vertex (geometry), vertices. The word circumsphere is sometimes used to mean the same thing, by analogy with the te ...
has radius (the circumradius)
:
and the inscribed sphere
image:Circumcentre.svg, An inscribed triangle of a circle
In geometry, an inscribed plane (geometry), planar shape or solid (geometry), solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figu ...
has radius
:
where ''V'' is the volume of the disphenoid and ''T'' is the area of any face, which is given by Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths Letting be the semiperimeter of the triangle, s = \tfrac12(a + b + c), the area is
A = \sqrt.
It is named after first-century ...
. There is also the following interesting relation connecting the volume and the circumradius:
:
The squares of the lengths of the bimedians are
:
Other properties
If the four faces of a tetrahedron have the same perimeter, then the tetrahedron is a disphenoid. If the four faces of a tetrahedron have the same area, then it is a disphenoid. The centers in the circumscribed andinscribed sphere
image:Circumcentre.svg, An inscribed triangle of a circle
In geometry, an inscribed plane (geometry), planar shape or solid (geometry), solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figu ...
s coincide with the centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-d ...
of the disphenoid.
The bimedians are perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', � ...
to the edges they connect and to each other.
Honeycombs and crystals
 Some tetragonal disphenoids will form
Some tetragonal disphenoids will form honeycomb
A honeycomb is a mass of Triangular prismatic honeycomb#Hexagonal prismatic honeycomb, hexagonal prismatic cells built from beeswax by honey bees in their beehive, nests to contain their brood (eggs, larvae, and pupae) and stores of honey and pol ...
s. The disphenoid whose four vertices are (−1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, −1) is such a disphenoid. Each of its four faces is an isosceles triangle with edges of lengths , , and 2. It can tessellate
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of ...
space to form the disphenoid tetrahedral honeycomb. As describes, it can be folded without cutting or overlaps from a single sheet of a4 paper
ISO 216 is an International Organization for Standardization, international standard for paper sizes, used around the world except in North America and parts of Latin America. The standard defines the "A", "B" and "C" series of paper sizes, wh ...
.
"Disphenoid" is also used to describe two forms of crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
:
* A wedge-shaped crystal form of the tetragonal
In crystallography, the tetragonal crystal system is one of the 7 crystal systems. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the Cube (geometry), cube becomes a rectangular Pri ...
or orthorhombic system. It has four triangular faces that are alike and that correspond in position to alternate faces of the tetragonal or orthorhombic dipyramid. It is symmetrical about each of three mutually perpendicular diad axes of symmetry in all classes except the tetragonal-disphenoidal, in which the form is generated by an inverse tetrad axis of symmetry.
* A crystal form bounded by eight scalene triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional ...
s arranged in pairs, constituting a tetragonal scalenohedron
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two pyramids together base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base vertices are usu ...
.
Other uses
Six tetragonal disphenoids attached end-to-end in a ring construct akaleidocycle
A kaleidocycle or flextangle is a flexible polyhedron connecting six tetrahedra (or tetragonal disphenoid, disphenoids) on opposite edges into a cycle. If the faces of the disphenoids are equilateral triangles, it can be constructed from a stretch ...
, a paper toy that can rotate on 4 sets of faces in a hexagon.
The rotation of the six disphenoids with opposite edges of length ''l'', ''m'' and ''n'' (without loss of generality
''Without loss of generality'' (often abbreviated to WOLOG, WLOG or w.l.o.g.; less commonly stated as ''without any loss of generality'' or ''with no loss of generality'') is a frequently used expression in mathematics. The term is used to indicat ...
''n'' ≤ ''l'', ''n'' ≤ ''m'') is physically realizable if and only if.
:
See also
* Irregular tetrahedra *Orthocentric tetrahedron
In geometry, an orthocentric tetrahedron is a tetrahedron where all three pairs of opposite edges are perpendicular. It is also known as an orthogonal tetrahedron since orthogonal means perpendicular. It was first studied by Simon Lhuilier in 1 ...
* Snub disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siame ...
- A Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
with 12 equilateral triangle faces and D2d symmetry.
* Trirectangular tetrahedron
In geometry, a trirectangular tetrahedron is a tetrahedron where all three face angles at one vertex are right angles. That vertex is called the ''right angle'' or ''apex'' of the trirectangular tetrahedron and the face opposite it is called ...
References
External links
Mathematical Analysis of Disphenoid by H C Rajpoot
from Academia.edu * * {{Mathworld , urlname=IsoscelesTetrahedron , title=Isosceles tetrahedron Tetrahedra