Digon on:
[Wikipedia]
[Google]
[Amazon]
In
Regular star figure 2(2,1).svg, A compound of two "line segment" digons, as the two possible alternations of a square (note the vertex arrangement).
Apeirogonal hosohedron.svg, The apeirogonal
Any straight-sided ''digon'' is regular even though it is degenerate, because its two edges are the same length and its two angles are equal (both being zero degrees). As such, the regular digon is a
Constructibility of Regular Polygons
, Iowa State University. (retrieved 20 December 2015) Some definitions of a polygon do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case.
 A digon as a
A digon as a
Regular digon in spherical geometry-2.svg, A lune on the sphere.
Hexagonal Hosohedron.svg, Six digon faces on a regular hexagonal
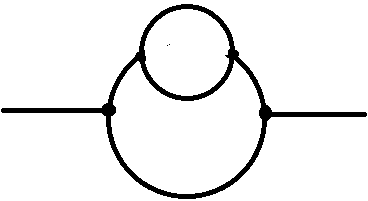 Digons (bigons) may be used in constructing and analyzing various topological structures, such as
Digons (bigons) may be used in constructing and analyzing various topological structures, such as
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a bigon, digon, or a ''2''-gon, is a polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
with two sides (edge
Edge or EDGE may refer to:
Technology Computing
* Edge computing, a network load-balancing system
* Edge device, an entry point to a computer network
* Adobe Edge, a graphical development application
* Microsoft Edge, a web browser developed by ...
s) and two vertices. Its construction is degenerate in a Euclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
because either the two sides would coincide or one or both would have to be curved; however, it can be easily visualised in elliptic space. It may also be viewed as a representation of a graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
with two vertices, see "Generalized polygon
In mathematics, a generalized polygon is an incidence structure introduced by Jacques Tits in 1959. Generalized ''n''-gons encompass as special cases projective planes (generalized triangles, ''n'' = 3) and generalized quadrangles (''n'' = 4). Ma ...
".
A regular digon has both angles equal and both sides equal and is represented by Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
. It may be constructed on a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
as a pair of 180 degree arcs connecting antipodal point
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its cen ...
s, when it forms a lune
Lune may refer to:
Rivers
*River Lune, in Lancashire and Cumbria, England
*River Lune, Durham, in County Durham, England
*Lune (Weser), a 43 km-long tributary of the Weser in Germany
*Lune River (Tasmania), in south-eastern Tasmania, Australia
Pl ...
.
The digon is the simplest abstract polytope
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.
A geometric polytope is said to be ...
of rank 2.
A truncated ''digon'', t is a square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
, . An alternated digon, h is a monogon
In geometry, a monogon, also known as a henagon, is a polygon with one Edge (geometry), edge and one Vertex (geometry), vertex. It has Schläfli symbol .Coxeter, ''Introduction to geometry'', 1969, Second edition, sec 21.3 ''Regular maps'', p. 386 ...
, .
In different fields
In Euclidean geometry
The digon can have one of two visual representations if placed in Euclidean space. One representation is degenerate, and visually appears as a double-covering of aline segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...
. Appearing when the minimum distance between the two edges is 0, this form arises in several situations. This double-covering form is sometimes used for defining degenerate cases of some other polytopes; for example, a regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
can be seen as an antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
formed of such a digon. It can be derived from the alternation of a square (h), as it requires two opposing vertices of said square to be connected. When higher-dimensional polytopes involving squares or other tetragonal figures are alternated, these digons are usually discarded and considered single edges.
A second visual representation, infinite in size, is as two parallel lines stretching to (and projectively meeting at; i.e. having vertices at) infinity, arising when the shortest distance between the two edges is greater than zero. This form arises in the representation of some degenerate polytopes, a notable example being the apeirogonal hosohedron, the limit of a general spherical hosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune ha ...
at infinity, composed of an infinite number of digons meeting at two antipodal points at infinity. However, as the vertices of these digons are at infinity and hence are not bound by closed line segments, this tessellation is usually not considered to be an additional regular tessellation of the Euclidean plane, even when its dual order-2 apeirogonal tiling (infinite dihedron) is.
hosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune ha ...
, containing infinitely narrow digons.
constructible polygon
In mathematics, a constructible polygon is a regular polygon that can be Compass and straightedge constructions, constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regu ...
.Eric T. EekhoffConstructibility of Regular Polygons
, Iowa State University. (retrieved 20 December 2015) Some definitions of a polygon do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case.
In elementary polyhedra
 A digon as a
A digon as a face
The face is the front of the head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect th ...
of a polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
is degenerate because it is a degenerate polygon, but sometimes it can have a useful topological existence in transforming polyhedra.
As a spherical lune
A spherical lune is a digon whose two vertices areantipodal points
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its cent ...
on the sphere.Coxeter (1973), Chapter 1, ''Polygons and Polyhedra'', pages 4 and 12.
A spherical polyhedron constructed from such digons is called a hosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune ha ...
.
hosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune ha ...
.
In topological structures
 Digons (bigons) may be used in constructing and analyzing various topological structures, such as
Digons (bigons) may be used in constructing and analyzing various topological structures, such as incidence structure
In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the Point (geometry), points and Line (geometry), lines of the Euclidean plane as t ...
s.
See also
*Monogon
In geometry, a monogon, also known as a henagon, is a polygon with one Edge (geometry), edge and one Vertex (geometry), vertex. It has Schläfli symbol .Coxeter, ''Introduction to geometry'', 1969, Second edition, sec 21.3 ''Regular maps'', p. 386 ...
* Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
* Demihypercube
References
Citations
Bibliography
* Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955 * Coxeter, ''Regular Polytopes'' (third edition), Dover Publications Inc, 1973 * *External links
* {{polygons Polygons by the number of sides 2 (number)