Coxeter Group on:
[Wikipedia]
[Google]
[Amazon]
In

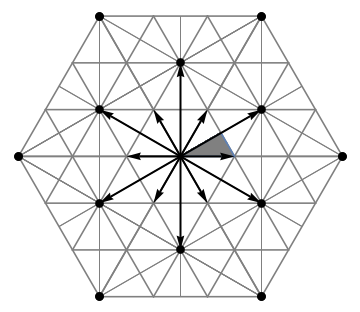 The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian
The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; for example, the symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
of each regular polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...
is a finite Coxeter group. However, not all Coxeter groups are finite, and not all can be described in terms of symmetries and Euclidean reflections. Coxeter groups were introduced in 1934 as abstractions of reflection groups, and finite Coxeter groups were classified in 1935.
Coxeter groups find applications in many areas of mathematics. Examples of finite Coxeter groups include the symmetry groups of regular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitive group action, transitively on its flag (geometry), flags, thus giving it the highest degree of symmetry. In particular, all its elements or -faces (for all , w ...
s, and the Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections t ...
s of simple Lie algebras. Examples of infinite Coxeter groups include the triangle groups corresponding to regular tessellations of the Euclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
and the hyperbolic plane, and the Weyl groups of infinite-dimensional Kac–Moody algebras.
Definition
Formally, a Coxeter group can be defined as a group with thepresentation
A presentation conveys information from a speaker to an audience. Presentations are typically demonstrations, introduction, lecture, or speech meant to inform, persuade, inspire, motivate, build goodwill, or present a new idea/product. Presenta ...
:
where and is either an integer or for .
Here, the condition means that no relation of the form for any integer should be imposed.
The pair where is a Coxeter group with generators is called a Coxeter system. Note that in general is ''not'' uniquely determined by . For example, the Coxeter groups of type and are isomorphic but the Coxeter systems are not equivalent, since the former has 3 generators and the latter has 1 + 3 = 4 generators (see below for an explanation of this notation).
A number of conclusions can be drawn immediately from the above definition.
* The relation means that for all ; as such the generators are involutions.
* If , then the generators and commute. This follows by observing that
::,
: together with
::
: implies that
::.
:Alternatively, since the generators are involutions, , so . That is to say, the commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.
Group theory
The commutator of two elements, ...
of and is equal to 1, or equivalently that and commute.
The reason that for is stipulated in the definition is that
:,
together with
:
already implies that
:.
An alternative proof of this implication is the observation that and are conjugates: indeed .
Coxeter matrix and Schläfli matrix
The Coxeter matrix is thesymmetric matrix
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,
Because equal matrices have equal dimensions, only square matrices can be symmetric.
The entries of a symmetric matrix are symmetric with ...
with entries . Indeed, every symmetric matrix with diagonal entries exclusively 1 and nondiagonal entries in the set is a Coxeter matrix.
The Coxeter matrix can be conveniently encoded by a Coxeter diagram, as per the following rules.
* The vertices of the graph are labelled by generator subscripts.
* Vertices and are adjacent if and only if .
* An edge is labelled with the value of whenever the value is or greater.
In particular, two generators commute if and only if they are not joined by an edge.
Furthermore, if a Coxeter graph has two or more connected components, the associated group is the direct product of the groups associated to the individual components.
Thus the disjoint union
In mathematics, the disjoint union (or discriminated union) A \sqcup B of the sets and is the set formed from the elements of and labelled (indexed) with the name of the set from which they come. So, an element belonging to both and appe ...
of Coxeter graphs yields a direct product of Coxeter groups.
The Coxeter matrix, , is related to the Schläfli matrix with entries , but the elements are modified, being proportional to the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
of the pairwise generators. The Schläfli matrix is useful because its eigenvalues
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
determine whether the Coxeter group is of ''finite type'' (all positive), ''affine type'' (all non-negative, at least one zero), or ''indefinite type'' (otherwise). The indefinite type is sometimes further subdivided, e.g. into hyperbolic and other Coxeter groups. However, there are multiple non-equivalent definitions for hyperbolic Coxeter groups.
An example
The graph in which vertices through are placed in a row with each vertex joined by an unlabelled edge to its immediate neighbors is the Coxeter diagram of thesymmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric grou ...
; the generators correspond to the transpositions . Any two non-consecutive transpositions commute, while multiplying two consecutive transpositions gives a 3-cycle : . Therefore is a quotient of the Coxeter group having Coxeter diagram . Further arguments show that this quotient map is an isomorphism.
Abstraction of reflection groups
Coxeter groups are an abstraction of reflection groups. Coxeter groups are ''abstract'' groups, in the sense of being given via a presentation. On the other hand, reflection groups are ''concrete'', in the sense that each of its elements is the composite of finitely many geometric reflections about linear hyperplanes in some euclidean space. Technically, a reflection group is a subgroup of alinear group In mathematics, a matrix group is a group ''G'' consisting of invertible matrices over a specified field ''K'', with the operation of matrix multiplication. A linear group is a group that is isomorphic to a matrix group (that is, admitting a ...
(or various generalizations) generated by orthogonal matrices of determinant -1. Each generator of a Coxeter group has order 2, which abstracts the geometric fact that performing a reflection twice is the identity. Each relation of the form , corresponding to the geometric fact that, given two hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
s meeting at an angle of , the composite of the two reflections about these hyperplanes is a rotation by , which has order ''k''.
In this way, every reflection group may be presented as a Coxeter group. The converse is partially true: every finite Coxeter group admits a faithful representation as a finite reflection group of some Euclidean space.
However, not every infinite Coxeter group admits a representation as a reflection group.
Finite Coxeter groups have been classified.
Finite Coxeter groups
Classification
Finite Coxeter groups are classified in terms of their Coxeter diagrams. The finite Coxeter groups with connected Coxeter diagrams consist of three one-parameter families of increasing dimension ( for , for , and for ), a one-parameter family of dimension two ( for ), and six exceptional groups ( and ). Every finite Coxeter group is the direct product of finitely many of these irreducible groups.Weyl groups
Many, but not all of these, are Weyl groups, and every Weyl group can be realized as a Coxeter group. The Weyl groups are the families and and the exceptions and denoted in Weyl group notation as The non-Weyl ones are the exceptions and and those members of the family that are not exceptionally isomorphic to a Weyl group (namely and ). This can be proven by comparing the restrictions on (undirected) Dynkin diagrams with the restrictions on Coxeter diagrams of finite groups: formally, the Coxeter graph can be obtained from the Dynkin diagram by discarding the direction of the edges, and replacing every double edge with an edge labelled 4 and every triple edge by an edge labelled 6. Also note that every finitely generated Coxeter group is an automatic group. Dynkin diagrams have the additional restriction that the only permitted edge labels are 2, 3, 4, and 6, which yields the above. Geometrically, this corresponds to the crystallographic restriction theorem, and the fact that excluded polytopes do not fill space or tile the plane – for the dodecahedron (dually, icosahedron) does not fill space; for the 120-cell (dually, 600-cell) does not fill space; for a ''p''-gon does not tile the plane except for or (the triangular, square, and hexagonal tilings, respectively). Note further that the (directed) Dynkin diagrams ''Bn'' and ''Cn'' give rise to the same Weyl group (hence Coxeter group), because they differ as ''directed'' graphs, but agree as ''undirected'' graphs – direction matters for root systems but not for the Weyl group; this corresponds to thehypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
and cross-polytope being different regular polytopes but having the same symmetry group.
Properties
Some properties of the finite irreducible Coxeter groups are given in the following table. The order of a reducible group can be computed by the product of its irreducible subgroup orders.Symmetry groups of regular polytopes
The symmetry group of every regular polytope is a finite Coxeter group. Note that dual polytopes have the same symmetry group. There are three series of regular polytopes in all dimensions. The symmetry group of a regular ''n''-simplex is the symmetric group ''S''''n''+1, also known as the Coxeter group of type ''An''. The symmetry group of the ''n''-cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
and its dual, the ''n''-cross-polytope, is ''Bn'', and is known as the hyperoctahedral group.
The exceptional regular polytopes in dimensions two, three, and four, correspond to other Coxeter groups. In two dimensions, the dihedral group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest example ...
s, which are the symmetry groups of regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s, form the series ''I''2(''p''), for ''p'' ≥ 3. In three dimensions, the symmetry group of the regular dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...
and its dual, the regular icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...
, is ''H''3, known as the full icosahedral group. In four dimensions, there are three exceptional regular polytopes, the 24-cell
In four-dimensional space, four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octa ...
, the 120-cell, and the 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol .
It is also known as the C600, hexacosichoron and hexacosihedroid.
It is also called a tetraplex (abbreviated from ...
. The first has symmetry group ''F''4, while the other two are dual and have symmetry group ''H''4.
The Coxeter groups of type ''D''''n'', ''E''6, ''E''7, and ''E''8 are the symmetry groups of certain semiregular polytopes.
Affine Coxeter groups
 The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian
The affine Coxeter groups form a second important series of Coxeter groups. These are not finite themselves, but each contains a normal abelian subgroup
In group theory, a branch of mathematics, a subset of a group G is a subgroup of G if the members of that subset form a group with respect to the group operation in G.
Formally, given a group (mathematics), group under a binary operation ...
such that the corresponding quotient group is finite. In each case, the quotient group is itself a Coxeter group, and the Coxeter graph of the affine Coxeter group is obtained from the Coxeter graph of the quotient group by adding another vertex and one or two additional edges. For example, for ''n'' ≥ 2, the graph consisting of ''n''+1 vertices in a circle is obtained from ''An'' in this way, and the corresponding Coxeter group is the affine Weyl group of ''An'' (the affine symmetric group). For ''n'' = 2, this can be pictured as a subgroup of the symmetry group of the standard tiling of the plane by equilateral triangles.
In general, given a root system, one can construct the associated '' Stiefel diagram'', consisting of the hyperplanes orthogonal to the roots along with certain translates of these hyperplanes. The affine Coxeter group (or affine Weyl group) is then the group generated by the (affine) reflections about all the hyperplanes in the diagram. The Stiefel diagram divides the plane into infinitely many connected components called ''alcoves'', and the affine Coxeter group acts freely and transitively on the alcoves, just as the ordinary Weyl group acts freely and transitively on the Weyl chambers. The figure at right illustrates the Stiefel diagram for the root system.
Suppose is an irreducible root system of rank and let be a collection of simple roots. Let, also, denote the highest root. Then the affine Coxeter group is generated by the ordinary (linear) reflections about the hyperplanes perpendicular to , together with an affine reflection about a translate of the hyperplane perpendicular to . The Coxeter graph for the affine Weyl group is the Coxeter–Dynkin diagram for , together with one additional node associated to . In this case, one alcove of the Stiefel diagram may be obtained by taking the fundamental Weyl chamber and cutting it by a translate of the hyperplane perpendicular to . Chapter 13, Exercises 12 and 13
A list of the affine Coxeter groups follows:
The group symbol subscript is one less than the number of nodes in each case, since each of these groups was obtained by adding a node to a finite group's graph.
Hyperbolic Coxeter groups
There are infinitely many hyperbolic Coxeter groups describing reflection groups in hyperbolic space, notably including the hyperbolic triangle groups.Irreducible Coxeter groups
A Coxeter group is said to be ''irreducible'' if its Coxeter–Dynkin diagram is connected. Every Coxeter group is the direct product of the irreducible groups that correspond to thecomponents
Component may refer to:
In engineering, science, and technology Generic systems
*System components, an entity with discrete structure, such as an assembly or software module, within a system considered at a particular level of analysis
* Lumped e ...
of its Coxeter–Dynkin diagram.
Partial orders
A choice of reflection generators gives rise to a length function ''ℓ'' on a Coxeter group, namely the minimum number of uses of generators required to express a group element; this is precisely the length in the word metric in theCayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
. An expression for ''v'' using ''ℓ''(''v'') generators is a ''reduced word''. For example, the permutation (13) in ''S''3 has two reduced words, (12)(23)(12) and (23)(12)(23). The function defines a map generalizing the sign map for the symmetric group.
Using reduced words one may define three partial order
In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word ''partial'' is used to indicate that not every pair of elements needs to be comparable ...
s on the Coxeter group, the (right) weak order, the absolute order and the Bruhat order (named for François Bruhat). An element ''v'' exceeds an element ''u'' in the Bruhat order if some (or equivalently, any) reduced word for ''v'' contains a reduced word for ''u'' as a substring, where some letters (in any position) are dropped. In the weak order, ''v'' ≥ ''u'' if some reduced word for ''v'' contains a reduced word for ''u'' as an initial segment. Indeed, the word length makes this into a graded poset
In mathematics, in the branch of combinatorics, a graded poset is a partially-ordered set (poset) ''P'' equipped with a rank function ''ρ'' from ''P'' to the set N of all natural number
In mathematics, the natural numbers are the numbers 0 ...
. The Hasse diagrams corresponding to these orders are objects of study, and are related to the Cayley graph
In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a Graph (discrete mathematics), graph that encodes the abstract structure of a group (mathematics), group. Its definition is sug ...
determined by the generators. The absolute order is defined analogously to the weak order, but with generating set/alphabet consisting of all conjugates of the Coxeter generators.
For example, the permutation (1 2 3) in ''S''3 has only one reduced word, (12)(23), so covers (12) and (23) in the Bruhat order but only covers (12) in the weak order.
Homology
Since a Coxeter group is generated by finitely many elements of order 2, its abelianization is an elementary abelian 2-group, i.e., it is isomorphic to the direct sum of several copies of thecyclic group
In abstract algebra, a cyclic group or monogenous group is a Group (mathematics), group, denoted C_n (also frequently \Z_n or Z_n, not to be confused with the commutative ring of P-adic number, -adic numbers), that is Generating set of a group, ge ...
. This may be restated in terms of the first homology group
In mathematics, the term homology, originally introduced in algebraic topology, has three primary, closely-related usages. The most direct usage of the term is to take the ''homology of a chain complex'', resulting in a sequence of abelian grou ...
of .
The Schur multiplier , equal to the second homology group of , was computed in for finite reflection groups and in for affine reflection groups, with a more unified account given in . In all cases, the Schur multiplier is also an elementary abelian 2-group. For each infinite family of finite or affine Weyl groups, the rank of stabilizes as goes to infinity.
See also
* Artin–Tits group * Chevalley–Shephard–Todd theorem *Complex reflection group
In mathematics, a complex reflection group is a Group (mathematics), finite group acting on a finite-dimensional vector space, finite-dimensional complex numbers, complex vector space that is generated by complex reflections: non-trivial elements t ...
* Coxeter element
* Iwahori–Hecke algebra, a quantum deformation of the group algebra
* Kazhdan–Lusztig polynomial
* Longest element of a Coxeter group
* Parabolic subgroup of a reflection group
* Supersolvable arrangement
* Isomorphism problem of Coxeter groups
Notes
References
Bibliography
* * * *Further reading
* * * * *External links
* * * {{DEFAULTSORT:Coxeter Group *