convex combination

In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average.

Formal definition

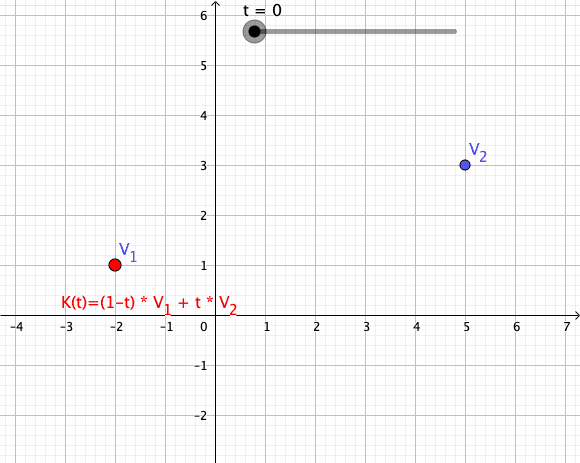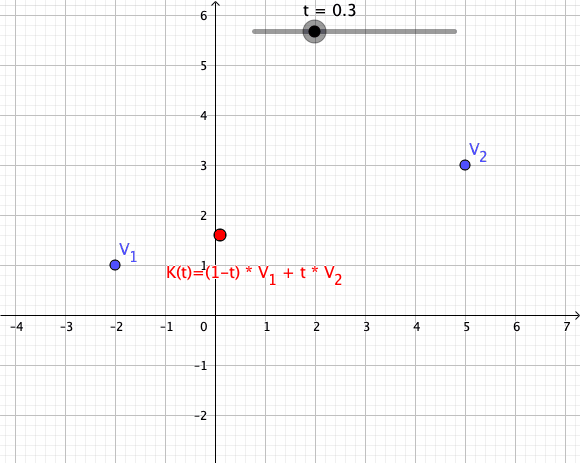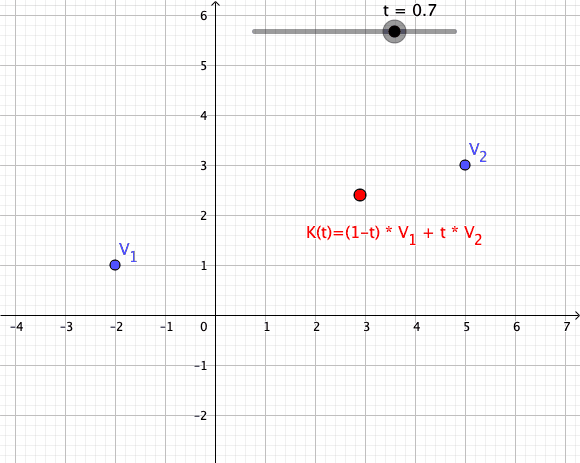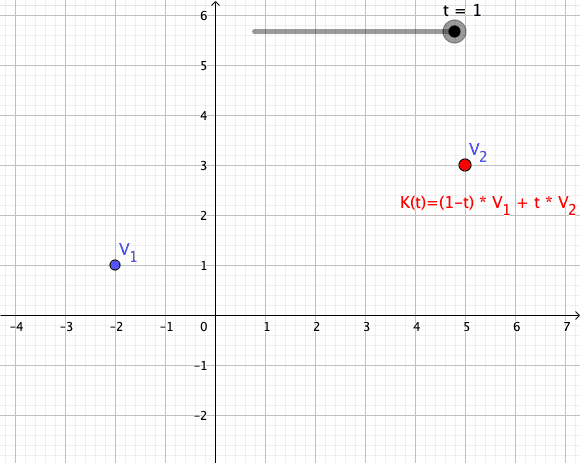
More formally, given a finite number of points $x_1, x_2, \dots, x_n$ in a real vector space, a convex combination of these points is a point of the form
: $\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n$
where the real numbers $\alpha_i$ satisfy $\alpha_i\ge 0$ and $\alpha_1+\alpha_2+\cdots+\alpha_n=1.$

As a particular example, every convex combination of two points lies on the line segment between the points.

A set is convex if it contains all convex combinations of its points.
The convex hull of a given set of points is identical to the set of all their convex combinations.

There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval ,1/math> is convex but generates the real-number line under linear combinations. Another example is the convex set of probability distributions, as linear combinations preserve neither nonnegativity nor affinity (i.e., having total integral one).

Other objects

* A random variable $X$ is said to have an $n$-component finite mixture distribution if its probability density function is a convex combination of $n$ so-called component densities.

Related constructions

* A conical combination is a linear combination with nonnegative coefficients. When a point $x$ is to be used as the reference origin for defining displacement vectors, then $x$ is a convex combination of $n$ points $x_1, x_2, \dots, x_n$ if and only if the zero displacement is a non-trivial conical combination of their $n$ respective displacement vectors relative to $x$.
* Weighted means are functionally the same as convex combinations, but they use a different notation. The coefficients ( weights) in a weighted mean are not required to sum to 1; instead the weighted linear combination is explicitly divided by the sum of the weights.
* Affine combinations are like convex combinations, but the coefficients are not required to be non-negative. Hence affine combinations are defined in vector spaces over any field.

See also

* Affine hull
* Carathéodory's theorem (convex hull)
* Simplex
* Barycentric coordinate system
* Convex space

References

External links

Convex sum/combination with a triangle
- interactive illustration
Convex sum/combination with a hexagon
- interactive illustration
Convex sum/combination with a tetraeder
- interactive illustration

{{DEFAULTSORT:Convex Combination
Convex geometry
Convex hulls
Mathematical analysis

de:Linearkombination#Konvexkombination