Circular error probable

Circular error probable (CEP),Circular Error Probable (CEP), Air Force Operational Test and Evaluation Center Technical Paper 6, Ver 2, July 1987, p. 1 also circular error probability or circle of equal probability, is a measure of a weapon system's precision in the military science of ballistics. It is defined as the radius of a circle, centered on the aimpoint, that is expected to enclose the landing points of 50% of the rounds; said otherwise, it is the median error radius, which is a 50% confidence interval. That is, if a given munitions design has a CEP of 100 m, when 100 munitions are targeted at the same point, an average of 50 will fall within a circle with a radius of 100 m about that point.

There are associated concepts, such as the DRMS (distance root mean square), which is the square root of the average squared distance error, a form of the standard deviation. Another is the R95, which is the radius of the circle where 95% of the values would fall, a 95% confidence interval.

The concept of CEP also plays a role when measuring the accuracy of a position obtained by a navigation system, such as GPS or older systems such as LORAN and Loran-C.

Concept

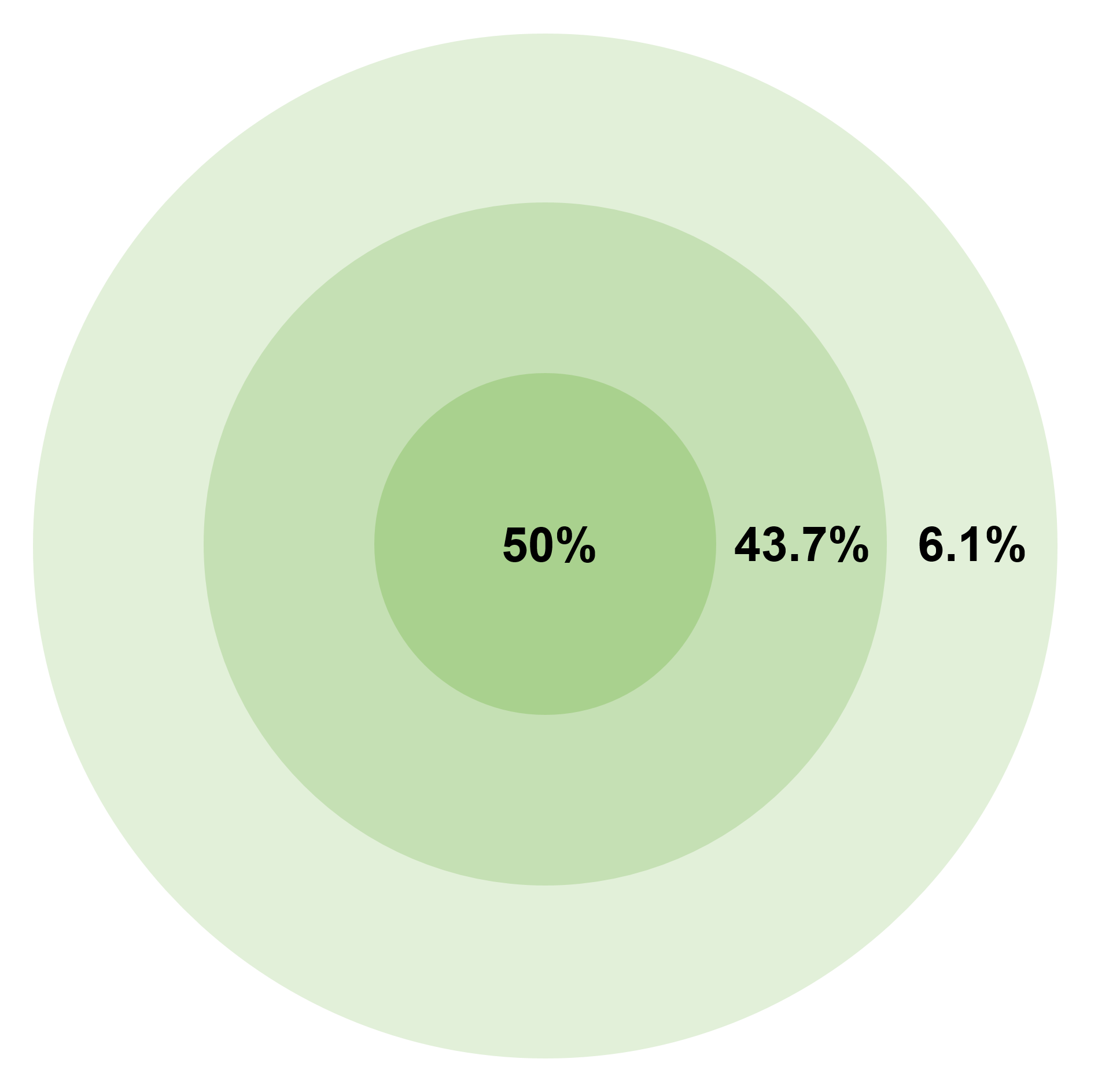
The original concept of CEP was based on a circular bivariate normal distribution (CBN) with CEP as a parameter of the CBN just as μ and σ are parameters of the normal distribution. Munitions with this distribution behavior tend to cluster around the mean impact point, with most reasonably close, progressively fewer and fewer further away, and very few at long distance. That is, if CEP is ''n'' metres, 50% of shots land within ''n'' metres of the mean impact, 43.7% between ''n'' and ''2n'', and 6.1% between ''2n'' and ''3n'' metres, and the proportion of shots that land farther than three times the CEP from the mean is only 0.2%.

CEP is not a good measure of accuracy when this distribution behavior is not met. Munitions may also have larger standard deviation of range errors than the standard deviation of azimuth (deflection) errors, resulting in an elliptical confidence region. Munition samples may not be exactly on target, that is, the mean vector will not be (0,0). This is referred to as bias.

To incorporate accuracy into the CEP concept in these conditions, CEP can be defined as the square root of the mean square error (MSE). The MSE will be the sum of the variance of the range error plus the variance of the azimuth error plus the covariance of the range error with the azimuth error plus the square of the bias. Thus the MSE results from pooling all these sources of error, geometrically corresponding to radius of a circle within which 50% of rounds will land.

Several methods have been introduced to estimate CEP from shot data. Included in these methods are the plug-in approach of Blischke and Halpin (1966), the Bayesian approach of Spall and Maryak (1992), and the maximum likelihood approach of Winkler and Bickert (2012). The Spall and Maryak approach applies when the shot data represent a mixture of different projectile characteristics (e.g., shots from multiple munitions types or from multiple locations directed at one target).

Conversion

While 50% is a very common definition for CEP, the circle dimension can be defined for percentages. Percentiles can be determined by recognizing that the horizontal position error is defined by a 2D vector which components are two orthogonal Gaussian random variables (one for each axis), assumed uncorrelated, each having a standard deviation $\sigma$. The ''distance error'' is the magnitude of that vector; it is a property of 2D Gaussian vectors that the magnitude follows the Rayleigh distribution, with scale factor $\sigma$. The ''distance root mean square'' (DRMS), is $\sigma_d=\sqrt\sigma$ and doubles as a sort of standard deviation, since errors within this value make up 63% of the sample represented by the bivariate circular distribution. In turn, the properties of the Rayleigh distribution are that its percentile at level F \in \%, 100\%/math> is given by the following formula:

:$Q(F, \sigma) = \sigma \sqrt$

or, expressed in terms of the DRMS:

:$Q(F, \sigma_d) = \sigma_d \frac$

The relation between $Q$ and $F$ are given by the following table, where the $F$ values for DRMS and 2DRMS (twice the distance root mean square) are specific to the Rayleigh distribution and are found numerically, while the CEP, R95 (95% radius) and R99.7 (99.7% radius) values are defined based on the 68–95–99.7 rule:

We can then derive a conversion table to convert values expressed for one percentile level, to another.Frank van Diggelen,
GPS Accuracy: Lies, Damn Lies, and Statistics
, ''GPS World'', Vol 9 No. 1, January 1998Frank van Diggelen, "GNSS Accuracy – Lies, Damn Lies and Statistics", ''GPS World'', Vol 18 No. 1, January 2007. Sequel to previous article with similar titl

/ref> Said conversion table, giving the coefficients $\alpha$ to convert $X$ into $Y=\alpha.X$, is given by:

For example, a GPS receiver having a 1.25 m DRMS will have a 1.25 m × 1.73 = 2.16 m 95% radius.

See also

* Probable error

References

Further reading

*
* Grubbs, F. E. (1964). "Statistical measures of accuracy for riflemen and missile engineers". Ann Arbor, ML: Edwards Brothers
Ballistipedia pdf
*
*
* Winkler, V. and Bickert, B. (2012). "Estimation of the circular error probability for a Doppler-Beam-Sharpening-Radar-Mode," in EUSAR. 9th European Conference on Synthetic Aperture Radar, pp. 368–71, 23/26 April 2012
ieeexplore.ieee.org
* Wollschläger, Daniel (2014), "Analyzing shape, accuracy, and precision of shooting results with shotGroups"
Reference manual for shotGroups
{{Refend

External links

Circular Error Probable
i
Ballistipedia

Applied probability
Military terminology
Aerial bombs
Artillery operation
Ballistics
Weapon guidance techniques
Accuracy and precision
Statistical distance
Combat modeling