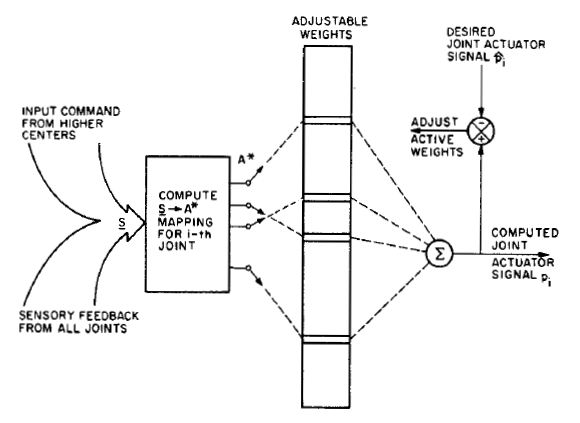The cerebellar model arithmetic computer (CMAC) is a type of neural network based on a model of the mammalian

cerebellum The cerebellum (Latin for "little brain") is a major feature of the hindbrain of all vertebrates. Although usually smaller than the cerebrum, in some animals such as the mormyrid fishes it may be as large as or even larger. In humans, the cerebel ...

. It is also known as the cerebellar model articulation controller. It is a type of

associative In mathematics, the associative property is a property of some binary operations, which means that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a valid rule of replacement f ...

memory Memory is the faculty of the mind by which data or information is encoded, stored, and retrieved when needed. It is the retention of information over time for the purpose of influencing future action. If past events could not be remembered, ...

. The CMAC was first proposed as a function modeler for robotic controllers by

James Albus James Sacra Albus (May 4, 1935 – April 17, 2011) was an American engineer, Senior NIST Fellow and founder and former chief of the Intelligent Systems Division of the Manufacturing Engineering Laboratory at the National Institute of Standards an ...

in 1975 (hence the name), but has been extensively used in reinforcement learning and also as for automated classification in the

machine learning Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine ...

community. The CMAC is an extension of the perceptron model. It computes a function for

n

input dimensions. The input space is divided up into hyper-rectangles, each of which is associated with a memory cell. The contents of the memory cells are the weights, which are adjusted during training. Usually, more than one quantisation of input space is used, so that any point in input space is associated with a number of hyper-rectangles, and therefore with a number of memory cells. The output of a CMAC is the algebraic sum of the weights in all the memory cells activated by the input point. A change of value of the input point results in a change in the set of activated hyper-rectangles, and therefore a change in the set of memory cells participating in the CMAC output. The CMAC output is therefore stored in a distributed fashion, such that the output corresponding to any point in input space is derived from the value stored in a number of memory cells (hence the name associative memory). This provides generalisation.

Building blocks

In the adjacent image, there are two inputs to the CMAC, represented as a 2D space. Two quantising functions have been used to divide this space with two overlapping grids (one shown in heavier lines). A single input is shown near the middle, and this has activated two memory cells, corresponding to the shaded area. If another point occurs close to the one shown, it will share some of the same memory cells, providing generalisation. The CMAC is trained by presenting pairs of input points and output values, and adjusting the weights in the activated cells by a proportion of the error observed at the output. This simple training algorithm has a proof of convergence. It is normal to add a kernel function to the hyper-rectangle, so that points falling towards the edge of a hyper-rectangle have a smaller activation than those falling near the centre. One of the major problems cited in practical use of CMAC is the memory size required, which is directly related to the number of cells used. This is usually ameliorated by using a hash function, and only providing memory storage for the actual cells that are activated by inputs.

One-step convergent algorithm

Initially least mean square (LMS) method is employed to update the weights of CMAC. The convergence of using LMS for training CMAC is sensitive to the learning rate and could lead to divergence. In 2004,Ting Qin, et al. "A learning algorithm of CMAC based on RLS." Neural Processing Letters 19.1 (2004): 49-61. a recursive least squares (RLS) algorithm was introduced to train CMAC online. It does not need to tune a learning rate. Its convergence has been proved theoretically and can be guaranteed to converge in one step. The computational complexity of this RLS algorithm is O(N3). Cmac

Hardware implementation infrastructure

Based on QR decomposition, an algorithm (QRLS) has been further simplified to have an O(N) complexity. Consequently, this reduces memory usage and time cost significantly. A parallel pipeline array structure on implementing this algorithm has been introduced.Ting Qin, et al. "Continuous CMAC-QRLS and its systolic array." Neural Processing Letters 22.1 (2005): 1-16. Overall by utilizing QRLS algorithm, the CMAC neural network convergence can be guaranteed, and the weights of the nodes can be updated using one step of training. Its parallel pipeline array structure offers its great potential to be implemented in hardware for large-scale industry usage.

Continuous CMAC

Since the rectangular shape of CMAC receptive field functions produce discontinuous staircase function approximation, by integrating CMAC with B-splines functions, continuous CMAC offers the capability of obtaining any order of derivatives of the approximate functions.

Deep CMAC

In recent years, numerous studies have confirmed that by stacking several shallow structures into a single deep structure, the overall system could achieve better data representation, and, thus, more effectively deal with nonlinear and high complexity tasks. In 2018,* Yu Tsao, et al. "Adaptive Noise Cancellation Using Deep Cerebellar Model Articulation Controller." IEEE Access Vol. 6, pp. 37395 - 37402, 2018. a deep CMAC (DCMAC) framework was proposed and a backpropagation algorithm was derived to estimate the DCMAC parameters. Experimental results of an adaptive noise cancellation task showed that the proposed DCMAC can achieve better noise cancellation performance when compared with that from the conventional single-layer CMAC.

Summary

References

{{reflist

External links

Blog on Cerebellar Model Articulation Controller (CMAC)
by Ting Qin. More details on the one-step convergent algorithm, code development, etc. Computational neuroscience Artificial neural networks Network architecture Networks