Box plot on:
[Wikipedia]
[Google]
[Amazon]
 In
In
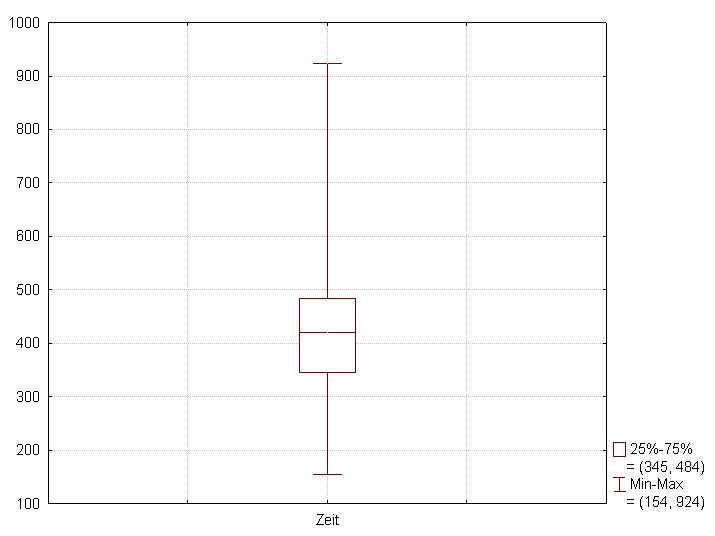
 A boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles.
*
A boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles.
*
 There are other representations in which the whiskers can stand for several other things, such as:
* One
There are other representations in which the whiskers can stand for several other things, such as:
* One
 Since the mathematician John W. Tukey first popularized this type of visual data display in 1969, several variations on the classical box plot have been developed, and the two most commonly found variations are the variable-width box plots and the notched box plots shown in Figure 4.
Variable-width box plots illustrate the size of each group whose data is being plotted by making the width of the box proportional to the size of the group. A popular convention is to make the box width proportional to the square root of the size of the group.
Notched box plots apply a "notch" or narrowing of the box around the median. Notches are useful in offering a rough guide of the significance of the difference of medians; if the notches of two boxes do not overlap, this will provide evidence of a statistically significant difference between the medians. The height of the notches is proportional to the interquartile range (IQR) of the sample and is inversely proportional to the square root of the size of the sample. However, there is an uncertainty about the most appropriate multiplier (as this may vary depending on the similarity of the variances of the samples). The width of the notch is arbitrarily chosen to be visually pleasing, and should be consistent amongst all box plots being displayed on the same page.
One convention for obtaining the boundaries of these notches is to use a distance of around the median.
Adjusted box plots are intended to describe skew distributions, and they rely on the medcouple statistic of skewness. For a medcouple value of MC, the lengths of the upper and lower whiskers on the box-plot are respectively defined to be:
:
For a symmetrical data distribution, the medcouple will be zero, and this reduces the adjusted box-plot to the Tukey's box-plot with equal whisker lengths of for both whiskers.
Other kinds of box plots, such as the violin plots and the bean plots can show the difference between single-modal and multimodal distributions, which cannot be observed from the original classical box-plot.
Since the mathematician John W. Tukey first popularized this type of visual data display in 1969, several variations on the classical box plot have been developed, and the two most commonly found variations are the variable-width box plots and the notched box plots shown in Figure 4.
Variable-width box plots illustrate the size of each group whose data is being plotted by making the width of the box proportional to the size of the group. A popular convention is to make the box width proportional to the square root of the size of the group.
Notched box plots apply a "notch" or narrowing of the box around the median. Notches are useful in offering a rough guide of the significance of the difference of medians; if the notches of two boxes do not overlap, this will provide evidence of a statistically significant difference between the medians. The height of the notches is proportional to the interquartile range (IQR) of the sample and is inversely proportional to the square root of the size of the sample. However, there is an uncertainty about the most appropriate multiplier (as this may vary depending on the similarity of the variances of the samples). The width of the notch is arbitrarily chosen to be visually pleasing, and should be consistent amongst all box plots being displayed on the same page.
One convention for obtaining the boundaries of these notches is to use a distance of around the median.
Adjusted box plots are intended to describe skew distributions, and they rely on the medcouple statistic of skewness. For a medcouple value of MC, the lengths of the upper and lower whiskers on the box-plot are respectively defined to be:
:
For a symmetrical data distribution, the medcouple will be zero, and this reduces the adjusted box-plot to the Tukey's box-plot with equal whisker lengths of for both whiskers.
Other kinds of box plots, such as the violin plots and the bean plots can show the difference between single-modal and multimodal distributions, which cannot be observed from the original classical box-plot.
 A series of hourly temperatures were measured throughout the day in degrees Fahrenheit. The recorded values are listed in order as follows (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
A box plot of the data set can be generated by first calculating five relevant values of this data set: minimum, maximum, median (''Q''2), first quartile (''Q''1), and third quartile (''Q''3).
The minimum is the smallest number of the data set. In this case, the minimum recorded day temperature is 57°F.
The maximum is the largest number of the data set. In this case, the maximum recorded day temperature is 81°F.
The median is the "middle" number of the ordered data set. This means that exactly 50% of the elements are below the median and 50% of the elements are greater than the median. The median of this ordered data set is 70°F.
The first quartile value (''Q''1 or 25th percentile) is the number that marks one quarter of the ordered data set. In other words, there are exactly 25% of the elements that are less than the first quartile and exactly 75% of the elements that are greater than it. The first quartile value can be easily determined by finding the "middle" number between the minimum and the median. For the hourly temperatures, the "middle" number found between 57°F and 70°F is 66°F.
The third quartile value (''Q''3 or 75th percentile) is the number that marks three quarters of the ordered data set. In other words, there are exactly 75% of the elements that are less than the third quartile and 25% of the elements that are greater than it. The third quartile value can be easily obtained by finding the "middle" number between the median and the maximum. For the hourly temperatures, the "middle" number between 70°F and 81°F is 75°F.
The interquartile range, or IQR, can be calculated by subtracting the first quartile value (''Q''1) from the third quartile value (''Q''3):
:
Hence,
1.5 IQR above the third quartile is:
:
1.5 IQR below the first quartile is:
:
The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Here, 1.5 IQR above the third quartile is 88.5°F and the maximum is 81°F. Therefore, the upper whisker is drawn at the value of the maximum, which is 81°F.
Similarly, the lower whisker boundary of the box plot is the smallest data value that is within 1.5 IQR below the first quartile. Here, 1.5 IQR below the first quartile is 52.5°F and the minimum is 57°F. Therefore, the lower whisker is drawn at the value of the minimum, which is 57°F.
A series of hourly temperatures were measured throughout the day in degrees Fahrenheit. The recorded values are listed in order as follows (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
A box plot of the data set can be generated by first calculating five relevant values of this data set: minimum, maximum, median (''Q''2), first quartile (''Q''1), and third quartile (''Q''3).
The minimum is the smallest number of the data set. In this case, the minimum recorded day temperature is 57°F.
The maximum is the largest number of the data set. In this case, the maximum recorded day temperature is 81°F.
The median is the "middle" number of the ordered data set. This means that exactly 50% of the elements are below the median and 50% of the elements are greater than the median. The median of this ordered data set is 70°F.
The first quartile value (''Q''1 or 25th percentile) is the number that marks one quarter of the ordered data set. In other words, there are exactly 25% of the elements that are less than the first quartile and exactly 75% of the elements that are greater than it. The first quartile value can be easily determined by finding the "middle" number between the minimum and the median. For the hourly temperatures, the "middle" number found between 57°F and 70°F is 66°F.
The third quartile value (''Q''3 or 75th percentile) is the number that marks three quarters of the ordered data set. In other words, there are exactly 75% of the elements that are less than the third quartile and 25% of the elements that are greater than it. The third quartile value can be easily obtained by finding the "middle" number between the median and the maximum. For the hourly temperatures, the "middle" number between 70°F and 81°F is 75°F.
The interquartile range, or IQR, can be calculated by subtracting the first quartile value (''Q''1) from the third quartile value (''Q''3):
:
Hence,
1.5 IQR above the third quartile is:
:
1.5 IQR below the first quartile is:
:
The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Here, 1.5 IQR above the third quartile is 88.5°F and the maximum is 81°F. Therefore, the upper whisker is drawn at the value of the maximum, which is 81°F.
Similarly, the lower whisker boundary of the box plot is the smallest data value that is within 1.5 IQR below the first quartile. Here, 1.5 IQR below the first quartile is 52.5°F and the minimum is 57°F. Therefore, the lower whisker is drawn at the value of the minimum, which is 57°F.
 Above is an example without outliers. Here is a follow-up example for generating box-plot with outliers:
The ordered set for the recorded temperatures is (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
In this example, only the first and the last number are changed. The median, third quartile, and first quartile remain the same.
In this case, the maximum value in this data set is 89°F, and 1.5 IQR above the third quartile is 88.5°F. The maximum is greater than 1.5 IQR plus the third quartile, so the maximum is an outlier. Therefore, the upper whisker is drawn at the greatest value smaller than 1.5 IQR above the third quartile, which is 79°F.
Similarly, the minimum value in this data set is 52°F, and 1.5 IQR below the first quartile is 52.5°F. The minimum is smaller than 1.5 IQR minus the first quartile, so the minimum is also an outlier. Therefore, the lower whisker is drawn at the smallest value greater than 1.5 IQR below the first quartile, which is 57°F.
Above is an example without outliers. Here is a follow-up example for generating box-plot with outliers:
The ordered set for the recorded temperatures is (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
In this example, only the first and the last number are changed. The median, third quartile, and first quartile remain the same.
In this case, the maximum value in this data set is 89°F, and 1.5 IQR above the third quartile is 88.5°F. The maximum is greater than 1.5 IQR plus the third quartile, so the maximum is an outlier. Therefore, the upper whisker is drawn at the greatest value smaller than 1.5 IQR above the third quartile, which is 79°F.
Similarly, the minimum value in this data set is 52°F, and 1.5 IQR below the first quartile is 52.5°F. The minimum is smaller than 1.5 IQR minus the first quartile, so the minimum is also an outlier. Therefore, the lower whisker is drawn at the smallest value greater than 1.5 IQR below the first quartile, which is 57°F.
descriptive statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and an ...
, a box plot or boxplot is a method for demonstrating graphically the locality, spread and skewness groups of numerical data through their quartile
In statistics, quartiles are a type of quantiles which divide the number of data points into four parts, or ''quarters'', of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are ...
s.
In addition to the box on a box plot, there can be lines (which are called ''whiskers'') extending from the box indicating variability outside the upper and lower quartiles, thus, the plot is also called the box-and-whisker plot and the box-and-whisker diagram. Outlier
In statistics, an outlier is a data point that differs significantly from other observations. An outlier may be due to a variability in the measurement, an indication of novel data, or it may be the result of experimental error; the latter are ...
s that differ significantly from the rest of the dataset may be plotted as individual points beyond the whiskers on the box-plot. Box plots are non-parametric
Nonparametric statistics is a type of statistical analysis that makes minimal assumptions about the underlying distribution of the data being studied. Often these models are infinite-dimensional, rather than finite dimensional, as in parametric sta ...
: they display variation in samples of a statistical population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hyp ...
without making any assumptions of the underlying statistical distribution
In statistics, an empirical distribution function ( an empirical cumulative distribution function, eCDF) is the distribution function associated with the empirical measure of a sample. This cumulative distribution function is a step functio ...
(though Tukey's boxplot assumes symmetry for the whiskers and normality for their length).
The spacings in each subsection of the box-plot indicate the degree of dispersion (spread) and skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal ...
of the data, which are usually described using the five-number summary. In addition, the box-plot allows one to visually estimate various L-estimator
In statistics, an L-estimator (or L-statistic) is an estimator which is a linear combination of order statistics of the measurements. This can be as little as a single point, as in the median (of an odd number of values), or as many as all points ...
s, notably the interquartile range
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the differen ...
, midhinge In statistics, the midhinge () is the average of the first and third quartiles and is thus a measure of location.
Equivalently, it is the 25% trimmed mid-range or 25% midsummary; it is an L-estimator. The midhinge is defined as \begin
\operato ...
, range
Range may refer to:
Geography
* Range (geographic), a chain of hills or mountains; a somewhat linear, complex mountainous or hilly area (cordillera, sierra)
** Mountain range, a group of mountains bordered by lowlands
* Range, a term used to i ...
, mid-range
In statistics, the mid-range or mid-extreme is a measure of central tendency of a sample defined as the arithmetic mean of the maximum and minimum values of the data set:
:M=\frac.
The mid-range is closely related to the range, a measure of ...
, and trimean In statistics the trimean (TM), or Tukey's trimean, is a measure of a probability distribution's location defined as a weighted average of the distribution's median and its two quartiles:
: TM= \frac
This is equivalent to the arithmetic mean of ...
. Box plots can be drawn either horizontally or vertically.
History
The range-bar method was first introduced by Mary Eleanor Spear in her book "Charting Statistics" in 1952 and again in her book "Practical Charting Techniques" in 1969. The box-and-whisker plot was first introduced in 1970 byJohn Tukey
John Wilder Tukey (; June 16, 1915 – July 26, 2000) was an American mathematician and statistician, best known for the development of the fast Fourier Transform (FFT) algorithm and box plot. The Tukey range test, the Tukey lambda distributi ...
, who later published on the subject in his book "Exploratory Data Analysis" in 1977.
Elements

 A boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles.
*
A boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles.
* Minimum
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative ...
(''Q''0 or 0th percentile
In statistics, a ''k''-th percentile, also known as percentile score or centile, is a score (e.g., a data point) a given percentage ''k'' of all scores in its frequency distribution exists ("exclusive" definition) or a score a given percentage ...
): the lowest data point in the data set excluding any outliers
* Maximum
In mathematical analysis, the maximum and minimum of a function (mathematics), function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given Interval (ma ...
(''Q''4 or 100th percentile): the highest data point in the data set excluding any outliers
* Median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
(''Q''2 or 50th percentile): the middle value in the data set
* First quartile
In statistics, quartiles are a type of quantiles which divide the number of data points into four parts, or ''quarters'', of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are ...
(''Q''1 or 25th percentile): also known as the ''lower quartile'' ''q''''n''(0.25), it is the median of the lower half of the dataset.
* Third quartile
In statistics, quartiles are a type of quantiles which divide the number of data points into four parts, or ''quarters'', of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are ...
(''Q''3 or 75th percentile): also known as the ''upper quartile'' ''q''''n''(0.75), it is the median of the upper half of the dataset.
In addition to the minimum and maximum values used to construct a box-plot, another important element that can also be employed to obtain a box-plot is the interquartile range (IQR), as denoted below:
* Interquartile range
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the differen ...
(IQR): the distance between the upper and lower quartiles
::
A box-plot usually includes two parts, a box and a set of whiskers as shown in Figure 2.
Box
The box is drawn from ''Q''1 to ''Q''3 with a horizontal line drawn inside it to denote the median. Some box plots include an additional character to represent the mean of the data.Whiskers
The whiskers must end at an observed data point, but can be defined in various ways. In the most straightforward method, the boundary of the lower whisker is the minimum value of the data set, and the boundary of the upper whisker is the maximum value of the data set. Because of this variability, it is appropriate to describe the convention that is being used for the whiskers and outliers in the caption of the box-plot. Another popular choice for the boundaries of the whiskers is based on the 1.5 IQR value. From above the upper quartile (''Q''3), a distance of 1.5 times the IQR is measured out and a whisker is drawn ''up to'' the largest observed data point from the dataset that falls within this distance. Similarly, a distance of 1.5 times the IQR is measured out below the lower quartile (''Q''1) and a whisker is drawn ''down to'' the lowest observed data point from the dataset that falls within this distance. Because the whiskers must end at an observed data point, the whisker lengths can look unequal, even though 1.5 IQR is the same for both sides. All other observed data points outside the boundary of the whiskers are plotted as outliers. The outliers can be plotted on the box-plot as a dot, a small circle, a star, ''etc.'' (see example below). There are other representations in which the whiskers can stand for several other things, such as:
* One
There are other representations in which the whiskers can stand for several other things, such as:
* One standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
above and below the mean of the data set
* The 9th percentile and the 91st percentile of the data set
* The 2nd percentile and the 98th percentile of the data set
Rarely, box-plot can be plotted without the whiskers. This can be appropriate for sensitive information to avoid whiskers (and outliers) disclosing actual values observed.
The unusual percentiles 2%, 9%, 91%, 98% are sometimes used for whisker cross-hatches and whisker ends to depict the seven-number summary In descriptive statistics, the seven-number summary is a collection of seven summary statistics, and is an extension of the five-number summary. There are three similar, common forms.
As with the five-number summary, it can be represented by a m ...
. If the data are normally distributed
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real number, real-valued random variable. The general form of its probability density function is
f(x ...
, the locations of the seven marks on the box plot will be equally spaced. On some box plots, a cross-hatch is placed before the end of each whisker.
Variations
Examples
Example without outliers
 A series of hourly temperatures were measured throughout the day in degrees Fahrenheit. The recorded values are listed in order as follows (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
A box plot of the data set can be generated by first calculating five relevant values of this data set: minimum, maximum, median (''Q''2), first quartile (''Q''1), and third quartile (''Q''3).
The minimum is the smallest number of the data set. In this case, the minimum recorded day temperature is 57°F.
The maximum is the largest number of the data set. In this case, the maximum recorded day temperature is 81°F.
The median is the "middle" number of the ordered data set. This means that exactly 50% of the elements are below the median and 50% of the elements are greater than the median. The median of this ordered data set is 70°F.
The first quartile value (''Q''1 or 25th percentile) is the number that marks one quarter of the ordered data set. In other words, there are exactly 25% of the elements that are less than the first quartile and exactly 75% of the elements that are greater than it. The first quartile value can be easily determined by finding the "middle" number between the minimum and the median. For the hourly temperatures, the "middle" number found between 57°F and 70°F is 66°F.
The third quartile value (''Q''3 or 75th percentile) is the number that marks three quarters of the ordered data set. In other words, there are exactly 75% of the elements that are less than the third quartile and 25% of the elements that are greater than it. The third quartile value can be easily obtained by finding the "middle" number between the median and the maximum. For the hourly temperatures, the "middle" number between 70°F and 81°F is 75°F.
The interquartile range, or IQR, can be calculated by subtracting the first quartile value (''Q''1) from the third quartile value (''Q''3):
:
Hence,
1.5 IQR above the third quartile is:
:
1.5 IQR below the first quartile is:
:
The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Here, 1.5 IQR above the third quartile is 88.5°F and the maximum is 81°F. Therefore, the upper whisker is drawn at the value of the maximum, which is 81°F.
Similarly, the lower whisker boundary of the box plot is the smallest data value that is within 1.5 IQR below the first quartile. Here, 1.5 IQR below the first quartile is 52.5°F and the minimum is 57°F. Therefore, the lower whisker is drawn at the value of the minimum, which is 57°F.
A series of hourly temperatures were measured throughout the day in degrees Fahrenheit. The recorded values are listed in order as follows (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
A box plot of the data set can be generated by first calculating five relevant values of this data set: minimum, maximum, median (''Q''2), first quartile (''Q''1), and third quartile (''Q''3).
The minimum is the smallest number of the data set. In this case, the minimum recorded day temperature is 57°F.
The maximum is the largest number of the data set. In this case, the maximum recorded day temperature is 81°F.
The median is the "middle" number of the ordered data set. This means that exactly 50% of the elements are below the median and 50% of the elements are greater than the median. The median of this ordered data set is 70°F.
The first quartile value (''Q''1 or 25th percentile) is the number that marks one quarter of the ordered data set. In other words, there are exactly 25% of the elements that are less than the first quartile and exactly 75% of the elements that are greater than it. The first quartile value can be easily determined by finding the "middle" number between the minimum and the median. For the hourly temperatures, the "middle" number found between 57°F and 70°F is 66°F.
The third quartile value (''Q''3 or 75th percentile) is the number that marks three quarters of the ordered data set. In other words, there are exactly 75% of the elements that are less than the third quartile and 25% of the elements that are greater than it. The third quartile value can be easily obtained by finding the "middle" number between the median and the maximum. For the hourly temperatures, the "middle" number between 70°F and 81°F is 75°F.
The interquartile range, or IQR, can be calculated by subtracting the first quartile value (''Q''1) from the third quartile value (''Q''3):
:
Hence,
1.5 IQR above the third quartile is:
:
1.5 IQR below the first quartile is:
:
The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Here, 1.5 IQR above the third quartile is 88.5°F and the maximum is 81°F. Therefore, the upper whisker is drawn at the value of the maximum, which is 81°F.
Similarly, the lower whisker boundary of the box plot is the smallest data value that is within 1.5 IQR below the first quartile. Here, 1.5 IQR below the first quartile is 52.5°F and the minimum is 57°F. Therefore, the lower whisker is drawn at the value of the minimum, which is 57°F.
Example with outliers
 Above is an example without outliers. Here is a follow-up example for generating box-plot with outliers:
The ordered set for the recorded temperatures is (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
In this example, only the first and the last number are changed. The median, third quartile, and first quartile remain the same.
In this case, the maximum value in this data set is 89°F, and 1.5 IQR above the third quartile is 88.5°F. The maximum is greater than 1.5 IQR plus the third quartile, so the maximum is an outlier. Therefore, the upper whisker is drawn at the greatest value smaller than 1.5 IQR above the third quartile, which is 79°F.
Similarly, the minimum value in this data set is 52°F, and 1.5 IQR below the first quartile is 52.5°F. The minimum is smaller than 1.5 IQR minus the first quartile, so the minimum is also an outlier. Therefore, the lower whisker is drawn at the smallest value greater than 1.5 IQR below the first quartile, which is 57°F.
Above is an example without outliers. Here is a follow-up example for generating box-plot with outliers:
The ordered set for the recorded temperatures is (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
In this example, only the first and the last number are changed. The median, third quartile, and first quartile remain the same.
In this case, the maximum value in this data set is 89°F, and 1.5 IQR above the third quartile is 88.5°F. The maximum is greater than 1.5 IQR plus the third quartile, so the maximum is an outlier. Therefore, the upper whisker is drawn at the greatest value smaller than 1.5 IQR above the third quartile, which is 79°F.
Similarly, the minimum value in this data set is 52°F, and 1.5 IQR below the first quartile is 52.5°F. The minimum is smaller than 1.5 IQR minus the first quartile, so the minimum is also an outlier. Therefore, the lower whisker is drawn at the smallest value greater than 1.5 IQR below the first quartile, which is 57°F.
In the case of large datasets
An additional example for obtaining box-plot from a data set containing a large number of data points is:General equation to compute empirical quantiles
: : :Here stands for the general ordering of the data points (i.e. if