Black's Median Voter Theorem on:
[Wikipedia]
[Google]
[Amazon]
In
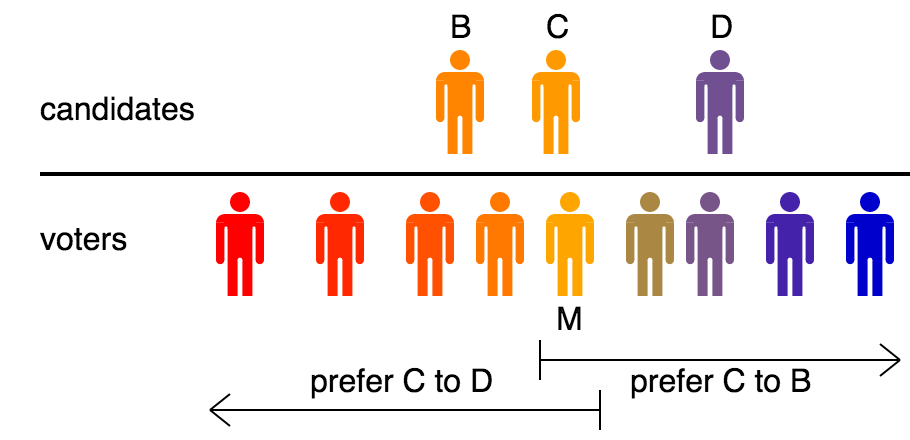 Say there is an election where candidates and voters have opinions distributed along a one-dimensional
Say there is an election where candidates and voters have opinions distributed along a one-dimensional
 The table shows an example of an election given by the
The table shows an example of an election given by the
 Despite this result, the median voter theorem can be applied to distributions that are rotationally symmetric, e.g. Gaussians, which have a single median that is the same in all directions. Whenever the distribution of voters has a unique median in all directions, and voters rank candidates in order of proximity, the median voter theorem applies: the candidate closest to the median will have a majority preference over all his or her rivals, and will be elected by any voting method satisfying the median voter property in one dimension.See Valerio Dotti's thesi
Despite this result, the median voter theorem can be applied to distributions that are rotationally symmetric, e.g. Gaussians, which have a single median that is the same in all directions. Whenever the distribution of voters has a unique median in all directions, and voters rank candidates in order of proximity, the median voter theorem applies: the candidate closest to the median will have a majority preference over all his or her rivals, and will be elected by any voting method satisfying the median voter property in one dimension.See Valerio Dotti's thesi
"Multidimensional Voting Models"
(2016). It follows that all median voter methods satisfy the same property in spaces of any dimension, for voter distributions with omnidirectional medians. It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem. ''Proof''. See the diagram, in which the grey disc represents the voter distribution as uniform over a circle and M is the median in all directions. Let A and B be two candidates, of whom A is the closer to the median. Then the voters who rank A above B are precisely the ones to the left (i.e. the 'A' side) of the solid red line; and since A is closer than B to M, the median is also to the left of this line. Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B.
Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B.
 ''Lemma''. Whenever a discrete distribution has a median ''M'' in all directions, the data points not located at ''M'' must come in balanced pairs (''A'',''A'' ' ) on either side of ''M'' with the property that ''A'' – ''M'' – ''A'' ' is a straight line (ie. ''not'' like ''A'' 0 – ''M'' – ''A'' 2 in the diagram).
''Proof''. This result was proved algebraically by Charles Plott in 1967. Here we give a simple geometric proof by contradiction in two dimensions.
Suppose, on the contrary, that there is a set of points ''Ai'' which have ''M'' as median in all directions, but for which the points not coincident with ''M'' do not come in balanced pairs. Then we may remove from this set any points at ''M'', and any balanced pairs about ''M'', without ''M'' ceasing to be a median in any direction; so ''M'' remains an omnidirectional median.
If the number of remaining points is odd, then we can easily draw a line through ''M'' such that the majority of points lie on one side of it, contradicting the median property of ''M''.
If the number is even, say 2''n'', then we can label the points ''A'' 0, ''A''1,... in clockwise order about ''M'' starting at any point (see the diagram). Let θ be the angle subtended by the arc from ''M'' –''A'' 0 to ''M'' –''A'' ''n'' . Then if θ < 180° as shown, we can draw a line similar to the broken red line through ''M'' which has the majority of data points on one side of it, again contradicting the median property of ''M'' ; whereas if θ > 180° the same applies with the majority of points on the other side. And if θ = 180°, then ''A'' 0 and ''A'' ''n'' form a balanced pair, contradicting another assumption.
''Theorem''. Whenever a discrete distribution has a median ''M'' in all directions, it coincides with its geometric median.
''Proof''. The sum of distances from any point ''P'' to a set of data points in balanced pairs (''A'',''A'' ' ) is the sum of the lengths ''A'' – ''P'' – ''A'' '. Each individual length of this form is minimized over ''P'' when the line is straight, as happens when ''P'' coincides with ''M''. The sum of distances from ''P'' to any data points located at ''M'' is likewise minimized when ''P'' and ''M'' coincide. Thus the sum of distances from the data points to ''P'' is minimized when ''P'' coincides with ''M''.
''Lemma''. Whenever a discrete distribution has a median ''M'' in all directions, the data points not located at ''M'' must come in balanced pairs (''A'',''A'' ' ) on either side of ''M'' with the property that ''A'' – ''M'' – ''A'' ' is a straight line (ie. ''not'' like ''A'' 0 – ''M'' – ''A'' 2 in the diagram).
''Proof''. This result was proved algebraically by Charles Plott in 1967. Here we give a simple geometric proof by contradiction in two dimensions.
Suppose, on the contrary, that there is a set of points ''Ai'' which have ''M'' as median in all directions, but for which the points not coincident with ''M'' do not come in balanced pairs. Then we may remove from this set any points at ''M'', and any balanced pairs about ''M'', without ''M'' ceasing to be a median in any direction; so ''M'' remains an omnidirectional median.
If the number of remaining points is odd, then we can easily draw a line through ''M'' such that the majority of points lie on one side of it, contradicting the median property of ''M''.
If the number is even, say 2''n'', then we can label the points ''A'' 0, ''A''1,... in clockwise order about ''M'' starting at any point (see the diagram). Let θ be the angle subtended by the arc from ''M'' –''A'' 0 to ''M'' –''A'' ''n'' . Then if θ < 180° as shown, we can draw a line similar to the broken red line through ''M'' which has the majority of data points on one side of it, again contradicting the median property of ''M'' ; whereas if θ > 180° the same applies with the majority of points on the other side. And if θ = 180°, then ''A'' 0 and ''A'' ''n'' form a balanced pair, contradicting another assumption.
''Theorem''. Whenever a discrete distribution has a median ''M'' in all directions, it coincides with its geometric median.
''Proof''. The sum of distances from any point ''P'' to a set of data points in balanced pairs (''A'',''A'' ' ) is the sum of the lengths ''A'' – ''P'' – ''A'' '. Each individual length of this form is minimized over ''P'' when the line is straight, as happens when ''P'' coincides with ''M''. The sum of distances from ''P'' to any data points located at ''M'' is likewise minimized when ''P'' and ''M'' coincide. Thus the sum of distances from the data points to ''P'' is minimized when ''P'' coincides with ''M''.
The Median Voter Model
Political science theories Public choice theory Voting theory Game theory Mathematical economics
political science
Political science is the scientific study of politics. It is a social science dealing with systems of governance and Power (social and political), power, and the analysis of political activities, political philosophy, political thought, polit ...
and social choice
Social choice theory is a branch of welfare economics that extends the theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures ( social welfare functions) used to combine i ...
, Black's median voter theorem says that if voters and candidates are distributed along a political spectrum
A political spectrum is a system to characterize and classify different Politics, political positions in relation to one another. These positions sit upon one or more Geometry, geometric Coordinate axis, axes that represent independent political ...
, any voting method compatible with majority-rule will elect the candidate preferred by the median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
voter. The median voter theorem thus shows that under a realistic model of voter behavior, Arrow's theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no Ordinal utility, ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Kenneth Arrow, Arrow showed no ...
does not apply, and rational choice is possible for societies. The theorem was first derived by Duncan Black in 1948, and independently by Kenneth Arrow
Kenneth Joseph Arrow (August 23, 1921 – February 21, 2017) was an American economist, mathematician and political theorist. He received the John Bates Clark Medal in 1957, and the Nobel Memorial Prize in Economic Sciences in 1972, along with ...
.
Voting rules without this median voter property, like ranked choice voting, plurality, and plurality-with-primaries have a center-squeeze effect that encourages candidates to take more extreme positions than the population would prefer. Similar median voter theorems exist for rules like score voting
Score voting, sometimes called range voting, is an electoral system for single-seat elections. Voters give each candidate a numerical score, and the candidate with the highest average score is elected. Score voting includes the well-known approva ...
and approval voting
Approval voting is a single-winner rated voting system where voters can approve of all the candidates as they like instead of Plurality voting, choosing one. The method is designed to eliminate vote-splitting while keeping election administration ...
when voters are either strategic and informed or if voters' ratings of candidates fall linearly with ideological distance.
An immediate consequence of Black's theorem, sometimes called the Hotelling-Downs median voter theorem, is that if the conditions for Black's theorem hold, politicians who only care about winning the election will adopt the same position as the median voter.Anthony Downs, " An Economic Theory of Democracy" (1957). However, this strategic convergence only occurs in voting systems that actually satisfy the median voter property ( see below).
Statement and proof of the theorem
 Say there is an election where candidates and voters have opinions distributed along a one-dimensional
Say there is an election where candidates and voters have opinions distributed along a one-dimensional political spectrum
A political spectrum is a system to characterize and classify different Politics, political positions in relation to one another. These positions sit upon one or more Geometry, geometric Coordinate axis, axes that represent independent political ...
. Voters rank candidates by proximity, i.e. the closest candidate is their first preference, the second-closest is their second preference, and so on. Then, the median voter theorem says that the candidate closest to the median voter is a ''majority-preferred'' (or ''Condorcet'') candidate. In other words, this candidate preferred to any one of their opponents by a majority of voters. When there are only two candidates, a simple majority vote
A majority is more than half of a total; however, the term is commonly used with other meanings, as explained in the "#Related terms, Related terms" section below.
It is a subset of a Set (mathematics), set consisting of more than half of the se ...
satisfies this condition, while for multi-candidate votes any majority-rule (Condorcet) method will satisfy it.
Proof sketch: Let the median
The median of a set of numbers is the value separating the higher half from the lower half of a Sample (statistics), data sample, a statistical population, population, or a probability distribution. For a data set, it may be thought of as the “ ...
voter be Marlene. The candidate who is closest to her will receive her first preference vote. Suppose that this candidate is Charles and that he lies to her left. Marlene and all voters to her left (by definition a majority of the electorate) will prefer Charles to all candidates to his right, and Marlene and all voters to her right (also a majority) will prefer Charles to all candidates to his left.
* The assumption that preferences are cast in order of proximity can be relaxed to say merely that they are single-peaked.
* The assumption that opinions lie along a real line can be relaxed to allow more general topologies.
* ''Spatial / valence models:'' Suppose that each candidate has a '' valence'' (attractiveness) in addition to his or her position in space, and suppose that voter ''i'' ranks candidates ''j'' in decreasing order of ''vj'' – ''dij'' where ''vj'' is ''j'' 's valence and ''dij'' is the distance from ''i'' to ''j''. Then the median voter theorem still applies: Condorcet methods will elect the candidate voted for by the median voter.
The median voter property
We will say that a voting method has the "median voter property in one dimension" if it always elects the candidate closest to the median voter under a one-dimensional spatial model. We may summarize the median voter theorem as saying that all Condorcet methods possess the median voter property in one dimension. It turns out that Condorcet methods are not unique in this:Coombs' method
Coombs' method is a ranked voting system. Like instant-runoff (IRV-RCV), Coombs' method is a sequential-loser method, where the last-place finisher according to one method is eliminated in each round. However, unlike in instant-runoff, each rou ...
is not Condorcet-consistent but nonetheless satisfies the median voter property in one dimension.B. Grofman and S. L. Feld, "If you like the alternative vote (a.k.a. the instant runoff), then you ought to know about the Coombs rule" (2004). Approval voting satisfies the same property under several models of strategic voting.
Extensions to higher dimensions
It is impossible to fully generalize the median voter theorem to spatial models in more than one dimension, as there is no longer a single unique "median" for all possible distributions of voters. However, it is still possible to demonstrate similar theorems under some limited conditions. The table shows an example of an election given by the
The table shows an example of an election given by the Marquis de Condorcet
Marie Jean Antoine Nicolas de Caritat, Marquis of Condorcet (; ; 17 September 1743 – 29 March 1794), known as Nicolas de Condorcet, was a French Philosophy, philosopher, Political economy, political economist, Politics, politician, and m ...
, who concluded it showed a problem with the Borda count
The Borda method or order of merit is a positional voting rule that gives each candidate a number of points equal to the number of candidates ranked below them: the lowest-ranked candidate gets 0 points, the second-lowest gets 1 point, and so on ...
.George G. Szpiro, "Numbers Rule" (2010). The Condorcet winner on the left is A, who is preferred to B by 41:40 and to C by 60:21. The Borda winner is instead B. However, Donald Saari constructs an example in two dimensions where the Borda count (but not the Condorcet winner) correctly identifies the candidate closest to the center (as determined by the geometric median
In geometry, the geometric median of a discrete point set in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances or absolute ...
).
The diagram shows a possible configuration of the voters and candidates consistent with the ballots, with the voters positioned on the circumference of a unit circle. In this case, A's mean absolute deviation is 1.15, whereas B's is 1.09 (and C's is 1.70), making B the spatial winner.
Thus the election is ambiguous in that two different spatial representations imply two different optimal winners. This is the ambiguity we sought to avoid earlier by adopting a median metric for spatial models; but although the median metric achieves its aim in a single dimension, the property does not fully generalize to higher dimensions.
Omnidirectional medians
"Multidimensional Voting Models"
(2016). It follows that all median voter methods satisfy the same property in spaces of any dimension, for voter distributions with omnidirectional medians. It is easy to construct voter distributions which do not have a median in all directions. The simplest example consists of a distribution limited to 3 points not lying in a straight line, such as 1, 2 and 3 in the second diagram. Each voter location coincides with the median under a certain set of one-dimensional projections. If A, B and C are the candidates, then '1' will vote A-B-C, '2' will vote B-C-A, and '3' will vote C-A-B, giving a Condorcet cycle. This is the subject of the McKelvey–Schofield theorem. ''Proof''. See the diagram, in which the grey disc represents the voter distribution as uniform over a circle and M is the median in all directions. Let A and B be two candidates, of whom A is the closer to the median. Then the voters who rank A above B are precisely the ones to the left (i.e. the 'A' side) of the solid red line; and since A is closer than B to M, the median is also to the left of this line.
 Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B.
Now, since M is a median in all directions, it coincides with the one-dimensional median in the particular case of the direction shown by the blue arrow, which is perpendicular to the solid red line. Thus if we draw a broken red line through M, perpendicular to the blue arrow, then we can say that half the voters lie to the left of this line. But since this line is itself to the left of the solid red line, it follows that more than half of the voters will rank A above B.
Relation between the median in all directions and the geometric median
Whenever a unique omnidirectional median exists, it determines the result of Condorcet voting methods. At the same time thegeometric median
In geometry, the geometric median of a discrete point set in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances or absolute ...
can arguably be identified as the ideal winner of a ranked preference election. It is therefore important to know the relationship between the two. In fact whenever a median in all directions exists (at least for the case of discrete distributions), it coincides with the geometric median.
Downsian model
The Downsian model (also called the Hotelling–Downs model) builds onHarold Hotelling
Harold Hotelling (; September 29, 1895 – December 26, 1973) was an American mathematical statistician and an influential economic theorist, known for Hotelling's law, Hotelling's lemma, and Hotelling's rule in economics, as well as Hotelling ...
's ''principle of minimum differentiation'', also known as ''Hotelling's law''. Anthony Downs
James Anthony Downs (November 21, 1930October 2, 2021) was an American economist specializing in public policy and public administration. His research focuses included political choice theory, rent control, affordable housing, and transportatio ...
adapted Hotelling's spatial competition framework to politics in 1957, creating a model that predicts politicians will converge to the median voter's position under four conditions:
# Candidates can choose ideological positions without consequence,
# Candidates only care about winning the election (not their actual beliefs),
# All other criteria of the median voter theorem are met (i.e. voters rank candidates by ideological distance),
# The voting system satisfies the median voter criterion.
As a special case, this law applies to the situation where there are exactly two candidates in the race, if it is impossible or implausible that any more candidates will join the race, because a simple majority vote between two alternatives satisfies the Condorcet criterion
A Condorcet winner (, ) is a candidate who would receive the support of more than half of the electorate in a one-on-one race against any one of their opponents. Voting systems where a majority winner will always win are said to satisfy the Condo ...
.
Hotelling's original principle was first described in 1929 for business competition, while Downs later applied this framework to electoral politics. In practice, none of these conditions hold for modern American elections, though they may have held in Hotelling's time (when nominees were often previously-unknown and chosen by closed party caucuses in ideologically diverse parties). Most importantly, politicians must win primary elections
Primary elections or primaries are elections held to determine which candidates will run in an upcoming general election. In a partisan primary, a political party selects a candidate. Depending on the state and/or party, there may be an "open pri ...
, which often include challengers or competitors, to be chosen as major-party nominees. As a result, politicians must compromise between appealing to the median voter in the primary and general electorates. Similar effects imply candidates do not converge to the median voter under electoral systems
An electoral or voting system is a set of rules used to determine the results of an election. Electoral systems are used in politics to elect governments, while non-political elections may take place in business, nonprofit organizations and inf ...
that do not satisfy the median voter theorem, including plurality voting
Plurality voting refers to electoral systems in which the candidates in an electoral district who poll more than any other (that is, receive a plurality) are elected.
Under single-winner plurality voting, and in systems based on single-member ...
, plurality-with-primaries, plurality-with-runoff, or ranked-choice runoff (RCV).
Uses of the median voter theorem
The theorem is valuable for the light it sheds on the optimality (and the limits to the optimality) of certain voting systems. Valerio Dotti points out broader areas of application:The ''Median Voter Theorem'' proved extremely popular in the Political Economy literature. The main reason is that it can be adopted to derive testable implications about the relationship between some characteristics of the voting population and the policy outcome, abstracting from other features of the political process.He adds that...
The median voter result has been applied to an incredible variety of questions. Examples are the analysis of the relationship between income inequality and size of governmental intervention in redistributive policies (Meltzer and Richard, 1981), the study of the determinants of immigration policies (Razin and Sadka, 1999), of the extent of taxation on different types of income (Bassetto and Benhabib, 2006), and many more.
Empirical evidence and contradictions
In theUnited States
The United States of America (USA), also known as the United States (U.S.) or America, is a country primarily located in North America. It is a federal republic of 50 U.S. state, states and a federal capital district, Washington, D.C. The 48 ...
Senate
A senate is a deliberative assembly, often the upper house or chamber of a bicameral legislature. The name comes from the ancient Roman Senate (Latin: ''Senatus''), so-called as an assembly of the senior (Latin: ''senex'' meaning "the el ...
, each state
State most commonly refers to:
* State (polity), a centralized political organization that regulates law and society within a territory
**Sovereign state, a sovereign polity in international law, commonly referred to as a country
**Nation state, a ...
is allocated two seats. Levitt (1996) examined the voting patterns of pairs of senators from the same state when one belonged to the Democratic Party and the other to the Republican Party. According to the Median Voter Theorem, the voting patterns of two senators representing the same state should be identical, regardless of party affiliation. However, reality differs. Moreover, Levitt found that the similarity in their voting patterns was only slightly higher than that of randomly paired senators. This finding suggests that senators' ideological leanings have a stronger influence on their decisions than voters' preferences, contradicting the prediction of the Median Voter Theorem.
Pande (2003) studied political changes in India
India, officially the Republic of India, is a country in South Asia. It is the List of countries and dependencies by area, seventh-largest country by area; the List of countries by population (United Nations), most populous country since ...
between 1960 and 1992 that increased political representation for marginalized groups. The data she collected showed that as a result of these changes, transfer payments to these populations increased even though the overall electorate (which had already included these groups) remained unchanged. This finding contradicts the Median Voter Theorem, as the model predicts that such a political shift should not alter the political equilibrium.
Chattopadhyay and Duflo (2004) examined another political change in India, which mandated that women lead one-third of village councils. These councils are responsible for providing various public goods to rural communities. According to the Median Voter Theorem, this policy should not have affected the composition of public goods
In economics, a public good (also referred to as a social good or collective good)Oakland, W. H. (1987). Theory of public goods. In Handbook of public economics (Vol. 2, pp. 485–535). Elsevier. is a goods, commodity, product or service that ...
supplied by local governments, as a female candidate still needs to be elected by a majority vote. As long as the median voter's preferences remain unchanged, the allocation of public goods should remain stable. However, empirical data showed that in villages where a woman was elected, the distribution of public goods shifted toward those preferred by women. Furthermore, in districts where women were elected for a second term, the allocation of public goods continued to reflect women's preferences. It is important to note, however, that while the composition of public goods changed when a woman led the village council, this does not necessarily imply an improvement or decline in overall social welfare.
Similar findings were reported by Miller (2008), who analyzed the impact of granting women the right to vote across the United States in 1920. Miller built on previous research indicating that women prioritize child welfare more than men and demonstrated that extending voting rights to women led to an immediate shift in federal policy. This change resulted in a significant increase in healthcare spending and a consequent reduction in child mortality rates by 8%–15%. However, unlike previous cases, Miller's findings actually support the Median Voter Theorem. This is because granting women suffrage altered the composition of the electorate, shifting the median voter’s position toward the preferences of the new female voters.
Lee, Moretti, and Butler (2004) investigated whether voters influence politicians' positions or merely choose from existing policy stances. They found that an exogenous shift in the voter base does not alter candidates' positions. For instance, an increase in Democratic voters in a given area does not push a Republican candidate’s stance further to the left, and vice versa. This finding suggests that the electorate selects from the positions that politicians already hold, rather than shaping those positions, contradicting the prediction of the Median Voter Theorem, which assumes candidates are ideologically neutral.
Gerber and Lewis (2015) analyzed voting data from a series of referendums in California
California () is a U.S. state, state in the Western United States that lies on the West Coast of the United States, Pacific Coast. It borders Oregon to the north, Nevada and Arizona to the east, and shares Mexico–United States border, an ...
to estimate the preferences of the median voter. They found that elected officials are constrained by the preferences of the median voter in homogeneous regions but less so in heterogeneous ones.
In contrast, Brunner and Ross (2010), who also studied voter data from two referendums in California, found that the decisive voter in votes concerning public expenditure was not the median voter, but rather a voter from the fourth income decile. This finding aligns with other studies suggesting that low-income voters often form coalitions with high-income voters to oppose increases in public spending.
Referendum data from Switzerland
Switzerland, officially the Swiss Confederation, is a landlocked country located in west-central Europe. It is bordered by Italy to the south, France to the west, Germany to the north, and Austria and Liechtenstein to the east. Switzerland ...
was used by Stadelmann, Portmann, and Eichenberger (2012) to examine the degree to which legislators' votes align with the preferences of the median voter in their districts. Their research showed that the Median Voter Model explains legislative voting behavior better than an alternative random voting hypothesis, but only by a modest margin of 17.6%. Additionally, they found that support from the median voter in a senator’s district increases the likelihood of the senator supporting a given proposal by 8.4% in parliament.
Milanovic (2000), using data from 79 countries, concluded that the greater the inequality in a country's pre-tax income distribution, the more aggressive the redistributive policies of the winning government. This finding supports the Median Voter Theorem.
See also
*Arrow's impossibility theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Arrow showed no such rule can satisfy the ind ...
* McKelvey–Schofield chaos theorem
* Median mechanism
* Ranked voting
Ranked voting is any voting system that uses voters' Ordinal utility, rankings of candidates to choose a single winner or multiple winners. More formally, a ranked vote system depends only on voters' total order, order of preference of the cand ...
* Median voting rule
Notes
References
Further reading
* * * * Dasgupta, Partha and Eric Maskin, "On the Robustness of Majority Rule", Journal of the European Economic Association, 2008. * * * * * * * * * * * {{cite journal , last=Waldfogel , first=Joel , title=The Median Voter and the Median Consumer: Local ''Private'' Goods and Population Composition , journal=Journal of Urban Economics
The ''Journal of Urban Economics'' is a bimonthly peer-reviewed academic journal covering urban economics. It is considered the premier journal in the field of urban economics. It was established in 1974 by Edwin Mills and is published by Elsevie ...
, year=2008 , volume=63 , issue=2 , pages=567–582 , doi=10.1016/j.jue.2007.04.002 , ssrn=878059 , s2cid=152378898
External links
The Median Voter Model
Political science theories Public choice theory Voting theory Game theory Mathematical economics