binary expansion on:
[Wikipedia]
[Google]
[Amazon]
A binary number is a
 The '' I Ching'' dates from the 9th century BC in China. The binary notation in the ''I Ching'' is used to interpret its
The '' I Ching'' dates from the 9th century BC in China. The binary notation in the ''I Ching'' is used to interpret its
/ref> Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows: : 0 0 0 1 numerical value 20 : 0 0 1 0 numerical value 21 : 0 1 0 0 numerical value 22 : 1 0 0 0 numerical value 23 While corresponding with the Jesuit priest Joachim Bouvet in 1700, who had made himself an expert on the ''I Ching'' while a missionary in China, Leibniz explained his binary notation, and Bouvet demonstrated in his 1701 letters that the ''I Ching'' was an independent, parallel invention of binary notation. Leibniz & Bouvet concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical
 In 1854, British mathematician
In 1854, British mathematician
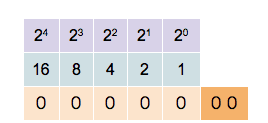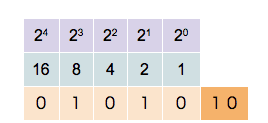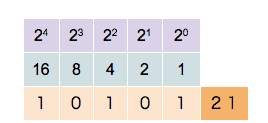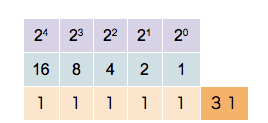
 Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant binary digit, or ''bit'' (the rightmost one, also called the ''first bit''), except that only the two symbols ''0'' and ''1'' are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:
:0000,
:0001, (rightmost bit starts over, and the next bit is incremented)
:0010, 0011, (rightmost two bits start over, and the next bit is incremented)
:0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)
:1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 20, the next representing 21, then 22, and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" bit. For example, the binary number 100101 is converted to decimal form as follows:
:1001012 = ( 1 ) × 25 + ( 0 ) × 24 + ( 0 ) × 23 + ( 1 ) × 22 + ( 0 ) × 21 + ( 1 ) × 20
:1001012 = 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
:1001012 = 3710
Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant binary digit, or ''bit'' (the rightmost one, also called the ''first bit''), except that only the two symbols ''0'' and ''1'' are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:
:0000,
:0001, (rightmost bit starts over, and the next bit is incremented)
:0010, 0011, (rightmost two bits start over, and the next bit is incremented)
:0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)
:1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 20, the next representing 21, then 22, and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" bit. For example, the binary number 100101 is converted to decimal form as follows:
:1001012 = ( 1 ) × 25 + ( 0 ) × 24 + ( 0 ) × 23 + ( 1 ) × 22 + ( 0 ) × 21 + ( 1 ) × 20
:1001012 = 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
:1001012 = 3710
1 1 1 0 1 1 1 1 1 0 cross out the "string",
+ 1 0 1 0 1 1 0 0 1 1 + 1 0 1 0 1 1 0 0 1 1 and cross out the digit that was added to it
——————————————————————— ——————————————————————
= 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1
The top row shows the carry bits used. Instead of the standard carry from one column to the next, the lowest-ordered "1" with a "1" in the corresponding place value beneath it may be added and a "1" may be carried to one digit past the end of the series. The "used" numbers must be crossed off, since they are already added. Other long strings may likewise be cancelled using the same technique. Then, simply add together any remaining digits normally. Proceeding in this manner gives the final answer of 1 1 0 0 1 1 1 0 0 0 12 (164910). In our simple example using small numbers, the traditional carry method required eight carry operations, yet the long carry method required only two, representing a substantial reduction of effort.
 To convert from a base-10
To convert from a base-10
Binary System
at
Conversion of Fractions
at
number
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
expressed in the base-2 numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
or binary numeral system, a method for representing number
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
s that uses only two symbols for the natural number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ...
s: typically "0" ( zero) and "1" ( one). A ''binary number'' may also refer to a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
that has a finite representation in the binary numeral system, that is, the quotient of an integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
by a power of two.
The base-2 numeral system is a positional notation
Positional notation, also known as place-value notation, positional numeral system, or simply place value, usually denotes the extension to any radix, base of the Hindu–Arabic numeral system (or decimal, decimal system). More generally, a posit ...
with a radix
In a positional numeral system, the radix (radices) or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, becaus ...
of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gate
A logic gate is a device that performs a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, one that has, for ...
s, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation.
History
The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, andGottfried Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Isaac Newton, Sir Isaac Newton, with the creation of calculus in ad ...
. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, Europe and India.
Egypt
The scribes of ancient Egypt used two different systems for their fractions, Egyptian fractions (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye ofHorus
Horus (), also known as Heru, Har, Her, or Hor () in Egyptian language, Ancient Egyptian, is one of the most significant ancient Egyptian deities who served many functions, most notably as the god of kingship, healing, protection, the sun, and t ...
, although this has been disputed). Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt, approximately 1200 BC.
The method used for ancient Egyptian multiplication is also closely related to binary numbers. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it; the order in which these steps are to be performed is given by the binary representation of the second number. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus, which dates to around 1650 BC.
China
quaternary
The Quaternary ( ) is the current and most recent of the three periods of the Cenozoic Era in the geologic time scale of the International Commission on Stratigraphy (ICS), as well as the current and most recent of the twelve periods of the ...
divination
Divination () is the attempt to gain insight into a question or situation by way of an occultic ritual or practice. Using various methods throughout history, diviners ascertain their interpretations of how a should proceed by reading signs, ...
technique.
It is based on taoistic duality of yin and yang
Originating in Chinese philosophy, yin and yang (, ), also yinyang or yin-yang, is the concept of opposite cosmic principles or forces that interact, interconnect, and perpetuate each other. Yin and yang can be thought of as complementary an ...
. Eight trigrams (Bagua) and a set of 64 hexagrams ("sixty-four" gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou dynasty
The Zhou dynasty ( ) was a royal dynasty of China that existed for 789 years from until 256 BC, the longest span of any dynasty in Chinese history. During the Western Zhou period (771 BC), the royal house, surnamed Ji, had military ...
of ancient China.
The Song dynasty
The Song dynasty ( ) was an Dynasties of China, imperial dynasty of China that ruled from 960 to 1279. The dynasty was founded by Emperor Taizu of Song, who usurped the throne of the Later Zhou dynasty and went on to conquer the rest of the Fiv ...
scholar Shao Yong (1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically. Viewing the least significant bit on top of single hexagrams in Shao Yong's square
and reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63.
Classical antiquity
Etruscans divided the outer edge of divination livers into sixteen parts, each inscribed with the name of a divinity and its region of the sky. Each liver region produced a binary reading which was combined into a final binary for divination. Divination at Ancient GreekDodona
Dodona (; , Ionic Greek, Ionic and , ) in Epirus in northwestern Greece was the oldest Ancient Greece, Hellenic oracle, possibly dating to the 2nd millennium BCE according to Herodotus. The earliest accounts in Homer describe Dodona as an oracle ...
oracle worked by drawing from separate jars, questions tablets and "yes" and "no" pellets. The result was then combined to make a final prophecy.
India
The Indian scholar Pingala (c. 2nd century BC) developed a binary system for describing prosody. He described meters in the form of short and long syllables (the latter equal in length to two short syllables). They were known as ''laghu'' (light) and ''guru'' (heavy) syllables. Pingala's Hindu classic titled Chandaḥśāstra (8.23) describes the formation of a matrix in order to give a unique value to each meter. "Chandaḥśāstra" literally translates to ''science of meters'' in Sanskrit. The binary representations in Pingala's system increases towards the right, and not to the left like in the binary numbers of the modernpositional notation
Positional notation, also known as place-value notation, positional numeral system, or simply place value, usually denotes the extension to any radix, base of the Hindu–Arabic numeral system (or decimal, decimal system). More generally, a posit ...
. In Pingala's system, the numbers start from number one, and not zero. Four short syllables "0000" is the first pattern and corresponds to the value one. The numerical value is obtained by adding one to the sum of place values.
Africa
The Ifá is an African divination system''.'' Similar to the ''I Ching'', but has up to 256 binary signs, unlike the ''I Ching'' which has 64. The Ifá originated in 15th century West Africa amongYoruba people
The Yoruba people ( ; , , ) are a West African ethnic group who inhabit parts of Nigeria, Benin, and Togo, which are collectively referred to as Yorubaland. The Yoruba constitute more than 50 million people in Africa, are over a million outsid ...
. In 2008, UNESCO
The United Nations Educational, Scientific and Cultural Organization (UNESCO ) is a List of specialized agencies of the United Nations, specialized agency of the United Nations (UN) with the aim of promoting world peace and International secur ...
added Ifá to its list of the "Masterpieces of the Oral and Intangible Heritage of Humanity
The Proclamation of Masterpieces of the Oral and Intangible Heritage of Humanity was made by the Director-General of UNESCO starting in 2001 to raise awareness of intangible cultural heritage—such traditions, rituals, dance, and knowledge—and ...
".
Other cultures
The residents of the island ofMangareva
Mangareva is the central and largest island of the Gambier Islands in French Polynesia. It is surrounded by smaller islands: Taravai in the southwest, Aukena and Akamaru in the southeast, and islands in the north. Mangareva has a permanent p ...
in French Polynesia
French Polynesia ( ; ; ) is an overseas collectivity of France and its sole #Governance, overseas country. It comprises 121 geographically dispersed islands and atolls stretching over more than in the Pacific Ocean, South Pacific Ocean. The t ...
were using a hybrid binary-decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
system before 1450. Slit drums with binary tones are used to encode messages across Africa and Asia.
Sets of binary combinations similar to the ''I Ching'' have also been used in traditional African divination systems, such as Ifá among others, as well as in medieval
In the history of Europe, the Middle Ages or medieval period lasted approximately from the 5th to the late 15th centuries, similarly to the post-classical period of World history (field), global history. It began with the fall of the West ...
Western geomancy
Geomancy, a compound of Greek roots denoting "earth divination", was originally used to mean methods of divination that interpret geographic features, markings on the ground, or the patterns formed by soil, rock (geology), rocks, or sand. Its d ...
. The majority of Indigenous Australian languages
The Indigenous languages of Australia number in the hundreds, the precise number being quite uncertain, although there is a range of estimates from a minimum of around 250 (using the technical definition of 'language' as non-mutually intellig ...
use a base-2 system.
Western predecessors to Leibniz
In the late 13th century Ramon Llull had the ambition to account for all wisdom in every branch of human knowledge of the time. For that purpose he developed a general method or "Ars generalis" based on binary combinations of a number of simple basic principles or categories, for which he has been considered a predecessor of computing science and artificial intelligence. In 1605,Francis Bacon
Francis Bacon, 1st Viscount St Alban (; 22 January 1561 – 9 April 1626) was an English philosopher and statesman who served as Attorney General and Lord Chancellor of England under King James I. Bacon argued for the importance of nat ...
discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text. Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: "provided those objects be capable of a twofold difference only; as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature".
(See Bacon's cipher.)
In 1617, John Napier
John Napier of Merchiston ( ; Latinisation of names, Latinized as Ioannes Neper; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8 ...
described a system he called location arithmetic for doing binary calculations using a non-positional representation by letters.
Thomas Harriot investigated several positional numbering systems, including binary, but did not publish his results; they were found later among his papers.
Possibly the first publication of the system in Europe was by Juan Caramuel y Lobkowitz, in 1700.
Leibniz
Leibniz wrote in excess of a hundred manuscripts on binary, most of them remaining unpublished. Before his first dedicated work in 1679, numerous manuscripts feature early attempts to explore binary concepts, including tables of numbers and basic calculations, often scribbled in the margins of works unrelated to mathematics. His first known work on binary, ''“On the Binary Progression"'', in 1679, Leibniz introduced conversion between decimal and binary, along with algorithms for performing basic arithmetic operations such as addition, subtraction, multiplication, and division using binary numbers. He also developed a form of binary algebra to calculate the square of a six-digit number and to extract square roots. His most well known work appears in his article ''Explication de l'Arithmétique Binaire'' (published in 1703). The full title of Leibniz's article is translated into English as the ''"Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi"''.Leibniz G., Explication de l'Arithmétique Binaire, Die Mathematische Schriften, ed. C. Gerhardt, Berlin 1879, vol.7, p.223; Engl. trans/ref> Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows: : 0 0 0 1 numerical value 20 : 0 0 1 0 numerical value 21 : 0 1 0 0 numerical value 22 : 1 0 0 0 numerical value 23 While corresponding with the Jesuit priest Joachim Bouvet in 1700, who had made himself an expert on the ''I Ching'' while a missionary in China, Leibniz explained his binary notation, and Bouvet demonstrated in his 1701 letters that the ''I Ching'' was an independent, parallel invention of binary notation. Leibniz & Bouvet concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
he admired. Of this parallel invention, Leibniz wrote in his "Explanation Of Binary Arithmetic" that "this restitution of their meaning, after such a great interval of time, will seem all the more curious."
The relation was a central idea to his universal concept of a language or characteristica universalis, a popular idea that would be followed closely by his successors such as Gottlob Frege
Friedrich Ludwig Gottlob Frege (; ; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic philos ...
and George Boole
George Boole ( ; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. H ...
in forming modern symbolic logic.
Leibniz was first introduced to the '' I Ching'' through his contact with the French Jesuit Joachim Bouvet, who visited China in 1685 as a missionary. Leibniz saw the ''I Ching'' hexagrams as an affirmation of the universality of his own religious beliefs as a Christian. Binary numerals were central to Leibniz's theology. He believed that binary numbers were symbolic of the Christian idea of '' creatio ex nihilo'' or creation out of nothing.
Later developments
 In 1854, British mathematician
In 1854, British mathematician George Boole
George Boole ( ; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. H ...
published a landmark paper detailing an algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
ic system of logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
that would become known as Boolean algebra. His logical calculus was to become instrumental in the design of digital electronic circuitry.
In 1937, Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, computer scientist, cryptographer and inventor known as the "father of information theory" and the man who laid the foundations of th ...
produced his master's thesis at MIT that implemented Boolean algebra and binary arithmetic using electronic relays and switches for the first time in history. Entitled '' A Symbolic Analysis of Relay and Switching Circuits'', Shannon's thesis essentially founded practical digital circuit
In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematica ...
design.
In November 1937, George Stibitz
George Robert Stibitz (April 30, 1904 – January 31, 1995) was an American researcher at Bell Labs who is internationally recognized as one of the fathers of the modern digital computer. He was known for his work in the 1930s and 1940s on the r ...
, then working at Bell Labs
Nokia Bell Labs, commonly referred to as ''Bell Labs'', is an American industrial research and development company owned by Finnish technology company Nokia. With headquarters located in Murray Hill, New Jersey, Murray Hill, New Jersey, the compa ...
, completed a relay-based computer he dubbed the "Model K" (for "Kitchen", where he had assembled it), which calculated using binary addition. Bell Labs authorized a full research program in late 1938 with Stibitz at the helm. Their Complex Number Computer, completed 8 January 1940, was able to calculate complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
. In a demonstration to the American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ...
conference at Dartmouth College
Dartmouth College ( ) is a Private university, private Ivy League research university in Hanover, New Hampshire, United States. Established in 1769 by Eleazar Wheelock, Dartmouth is one of the nine colonial colleges chartered before the America ...
on 11 September 1940, Stibitz was able to send the Complex Number Calculator remote commands over telephone lines by a teletype. It was the first computing machine ever used remotely over a phone line. Some participants of the conference who witnessed the demonstration were John von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, in ...
, John Mauchly
John William Mauchly ( ; August 30, 1907 – January 8, 1980) was an American physicist who, along with J. Presper Eckert, designed ENIAC, the first general-purpose electronic digital computer, as well as EDVAC, BINAC and UNIVAC I, the f ...
and Norbert Wiener
Norbert Wiener (November 26, 1894 – March 18, 1964) was an American computer scientist, mathematician, and philosopher. He became a professor of mathematics at the Massachusetts Institute of Technology ( MIT). A child prodigy, Wiener late ...
, who wrote about it in his memoirs.
The Z1 computer, which was designed and built by Konrad Zuse between 1935 and 1938, used Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variable (mathematics), variables are the truth values ''true'' and ''false'', usually denot ...
and binary floating-point numbers. (12 pages)
Representation
Any number can be represented by a sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667: The numeric value represented in each case depends on the value assigned to each symbol. In the earlier days of computing, switches, punched holes, and punched paper tapes were used to represent binary values. In a modern computer, the numeric values may be represented by two differentvoltage
Voltage, also known as (electrical) potential difference, electric pressure, or electric tension, is the difference in electric potential between two points. In a Electrostatics, static electric field, it corresponds to the Work (electrical), ...
s; on a magnetic disk, magnetic polarities may be used. A "positive", " yes", or "on" state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.
In keeping with the customary representation of numerals using Arabic numerals
The ten Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are the most commonly used symbols for writing numbers. The term often also implies a positional notation number with a decimal base, in particular when contrasted with Roman numera ...
, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed, or suffixed to indicate their base, or radix
In a positional numeral system, the radix (radices) or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, becaus ...
. The following notations are equivalent:
* 100101 binary (explicit statement of format)
* 100101b (a suffix indicating binary format; also known as Intel convention)
* 100101B (a suffix indicating binary format)
* bin 100101 (a prefix indicating binary format)
* 1001012 (a subscript indicating base-2 (binary) notation)
* %100101 (a prefix indicating binary format; also known as Motorola convention)
* 0b100101 (a prefix indicating binary format, common in programming languages)
* 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
* #b100101 (a prefix indicating binary format, common in Lisp programming languages)
When spoken, binary numerals are usually read digit-by-digit, to distinguish them from decimal numerals. For example, the binary numeral 100 is pronounced ''one zero zero'', rather than ''one hundred'', to make its binary nature explicit and for purposes of correctness. Since the binary numeral 100 represents the value four, it would be confusing to refer to the numeral as ''one hundred'' (a word that represents a completely different value, or amount). Alternatively, the binary numeral 100 can be read out as "four" (the correct ''value''), but this does not make its binary nature explicit.
Counting in binary
Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiardecimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
counting system as a frame of reference.
Decimal counting
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
counting uses the ten symbols ''0'' through ''9''. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the ''first digit''. When the available symbols for this position are exhausted, the least significant digit is reset to ''0'', and the next digit of higher significance (one position to the left) is incremented (''overflow''), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows:
:000, 001, 002, ... 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented)
:010, 011, 012, ...
: ...
:090, 091, 092, ... 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented)
:100, 101, 102, ...
Binary counting

Fractions
Fractions in binary arithmetic terminate only if the denominator is a power of 2. As a result, 1/10 does not have a finite binary representation (10 has prime factors 2 and 5). This causes 10 × 1/10 not to precisely equal 1 in binaryfloating-point arithmetic
In computing, floating-point arithmetic (FP) is arithmetic on subsets of real numbers formed by a ''significand'' (a Sign (mathematics), signed sequence of a fixed number of digits in some Radix, base) multiplied by an integer power of that ba ...
. As an example, to interpret the binary expression for 1/3 = .010101..., this means: 1/3 = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + ... = 0.3125 + ... An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.
Binary arithmetic
Arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
in binary is much like arithmetic in other positional notation
Positional notation, also known as place-value notation, positional numeral system, or simply place value, usually denotes the extension to any radix, base of the Hindu–Arabic numeral system (or decimal, decimal system). More generally, a posit ...
numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
s. Addition, subtraction, multiplication, and division can be performed on binary numerals.
Addition
The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying: :0 + 0 → 0 :0 + 1 → 1 :1 + 0 → 1 :1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 21) ) Adding two "1" digits produces a digit "0", while 1 will have to be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented: :5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 101) ) :7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 101) ) This is known as ''carrying''. When the result of an addition exceeds the value of a digit, the procedure is to "carry" the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary: 0 1 1 0 1 + 1 0 1 1 1 ------------- = 1 0 0 1 0 0 = 36 In this example, two numerals are being added together: 011012 (1310) and 101112 (2310). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 102. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 102 again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 112. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 1001002 (3610). When computers must add two numbers, the rule that: x xor y = (x + y) mod 2 for any two bits x and y allows for very fast calculation, as well.Long carry method
A simplification for many binary addition problems is the "long carry method" or "Brookhouse Method of Binary Addition". This method is particularly useful when one of the numbers contains a long stretch of ones. It is based on the simple premise that under the binary system, when given a stretch of digits composed entirely of ones (where is any integer length), adding 1 will result in the number 1 followed by a string of zeros. That concept follows, logically, just as in the decimal system, where adding 1 to a string of 9s will result in the number 1 followed by a string of 0s: Binary Decimal 1 1 1 1 1 likewise 9 9 9 9 9 + 1 + 1 ——————————— ——————————— 1 0 0 0 0 0 1 0 0 0 0 0 Such long strings are quite common in the binary system. From that one finds that large binary numbers can be added using two simple steps, without excessive carry operations. In the following example, two numerals are being added together: 1 1 1 0 1 1 1 1 1 02 (95810) and 1 0 1 0 1 1 0 0 1 12 (69110), using the traditional carry method on the left, and the long carry method on the right: Traditional Carry Method Long Carry Method vs. carry the 1 until it is one digit past the "string" below 1 1 1 0 1 1 1 1 1 0Addition table
The binary addition table is similar to, but not the same as, thetruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
of the logical disjunction
In logic, disjunction (also known as logical disjunction, logical or, logical addition, or inclusive disjunction) is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is ...
operation . The difference is that , while .
Subtraction
Subtraction works in much the same way: :0 − 0 → 0 :0 − 1 → 1, borrow 1 :1 − 0 → 1 :1 − 1 → 0 Subtracting a "1" digit from a "0" digit produces the digit "1", while 1 will have to be subtracted from the next column. This is known as ''borrowing''. The principle is the same as for carrying. When the result of a subtraction is less than 0, the least possible value of a digit, the procedure is to "borrow" the deficit divided by the radix (that is, 10/10) from the left, subtracting it from the next positional value. * * * * (starred columns are borrowed from) 1 1 0 1 1 1 0 − 1 0 1 1 1 ---------------- = 1 0 1 0 1 1 1 * (starred columns are borrowed from) 1 0 1 1 1 1 1 – 1 0 1 0 1 1 ---------------- = 0 1 1 0 1 0 0 Subtracting a positive number is equivalent to ''adding'' anegative number
In mathematics, a negative number is the opposite (mathematics), opposite of a positive real number. Equivalently, a negative number is a real number that is inequality (mathematics), less than 0, zero. Negative numbers are often used to represe ...
of equal absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
. Computers use signed number representations
In computing, signed number representations are required to encode negative numbers in binary number systems.
In mathematics, negative numbers in any base are represented by prefixing them with a minus sign ("−"). However, in RAM or CPU reg ...
to handle negative numbers—most commonly the two's complement notation. Such representations eliminate the need for a separate "subtract" operation. Using two's complement notation, subtraction can be summarized by the following formula:
:
Multiplication
Multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
in binary is similar to its decimal counterpart. Two numbers and can be multiplied by partial products: for each digit in , the product of that digit in is calculated and written on a new line, shifted leftward so that its rightmost digit lines up with the digit in that was used. The sum of all these partial products gives the final result.
Since there are only two digits in binary, there are only two possible outcomes of each partial multiplication:
* If the digit in is 0, the partial product is also 0
* If the digit in is 1, the partial product is equal to
For example, the binary numbers 1011 and 1010 are multiplied as follows:
1 0 1 1 ()
× 1 0 1 0 ()
---------
0 0 0 0 ← to the rightmost 'zero' in
+ 1 0 1 1 ← to the next 'one' in
+ 0 0 0 0
+ 1 0 1 1
---------------
= 1 1 0 1 1 1 0
Binary numbers can also be multiplied with bits after a binary point:
1 0 1 . 1 0 1 (5.625 in decimal)
× 1 1 0 . 0 1 (6.25 in decimal)
-------------------
1 . 0 1 1 0 1 ← to a 'one' in
+ 0 0 . 0 0 0 0 ← to a 'zero' in
+ 0 0 0 . 0 0 0
+ 1 0 1 1 . 0 1
+ 1 0 1 1 0 . 1
---------------------------
= 1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)
See also Booth's multiplication algorithm.
Multiplication table
The binary multiplication table is the same as thetruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arg ...
of the logical conjunction
In logic, mathematics and linguistics, ''and'' (\wedge) is the Truth function, truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as \wedge or \& or K (prefix) or ...
operation .
Division
Long division in binary is again similar to its decimal counterpart. In the example below, the divisor is 1012, or 5 in decimal, while thedividend
A dividend is a distribution of profits by a corporation to its shareholders, after which the stock exchange decreases the price of the stock by the dividend to remove volatility. The market has no control over the stock price on open on the ex ...
is 110112, or 27 in decimal. The procedure is the same as that of decimal long division; here, the divisor 1012 goes into the first three digits 1102 of the dividend one time, so a "1" is written on the top line. This result is multiplied by the divisor, and subtracted from the first three digits of the dividend; the next digit (a "1") is included to obtain a new three-digit sequence:
1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
0 0 1
The procedure is then repeated with the new sequence, continuing until the digits in the dividend have been exhausted:
1 0 1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
1 1 1
− 1 0 1
-----
0 1 0
Thus, the quotient of 110112 divided by 1012 is 1012, as shown on the top line, while the remainder, shown on the bottom line, is 102. In decimal, this corresponds to the fact that 27 divided by 5 is 5, with a remainder of 2.
Aside from long division, one can also devise the procedure so as to allow for over-subtracting from the partial remainder at each iteration, thereby leading to alternative methods which are less systematic, but more flexible as a result.
Square root
The process of taking a binary square root digit by digit is essentially the same as for a decimal square root but much simpler, due to the binary nature. First group the digits in pairs, using a leading 0 if necessary so there are an even number of digits. Now at each step, consider the answer so far, extended with the digits 01. If this can be subtracted from the current remainder, do so. Then extend the remainder with the next pair of digits. If you subtracted, the next digit of the answer is 1, otherwise it's 0. 1 1 1 1 1 0 1 1 0 1 ------------- ------------- ------------- ------------- ------------- √ 10 10 10 01 √ 10 10 10 01 √ 10 10 10 01 √ 10 10 10 01 √ 10 10 10 01 - 1 - 1 - 1 - 1 Answer so far is 0, ---- ---- ---- ---- extended by 01 is 001, 1 10 1 10 1 10 1 10 this CAN be subtracted - 1 01 - 1 01 - 1 01 from first pair 10, Answer so far is 1, ------- ------- ------- so first digit of extended by 01 is 101, 1 10 1 10 01 1 10 01 answer is 1. this CAN be subtracted - 1 10 01 from remainder 110, so Answer so far is 11, Answer so far is 110, ---------- next answer digit is 1. extended by 01 is 1101, extended by 01 is 11001, 0 this is TOO BIG to this CAN be subtracted subtract from remainder from remainder 11001, so Done! 110, so next digit of next digit of answer is 1. answer is 0.Bitwise operations
Though not directly related to the numerical interpretation of binary symbols, sequences of bits may be manipulated using Boolean logical operators. When a string of binary symbols is manipulated in this way, it is called abitwise operation
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operatio ...
; the logical operators AND, OR, and XOR may be performed on corresponding bits in two binary numerals provided as input. The logical NOT operation may be performed on individual bits in a single binary numeral provided as input. Sometimes, such operations may be used as arithmetic short-cuts, and may have other computational benefits as well. For example, an arithmetic shift left of a binary number is the equivalent of multiplication by a (positive, integral) power of 2.
Conversion to and from other numeral systems
Decimal to binary
 To convert from a base-10
To convert from a base-10 integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
to its base-2 (binary) equivalent, the number is divided by two. The remainder is the least-significant bit. The quotient is again divided by two; its remainder becomes the next least significant bit. This process repeats until a quotient of one is reached. The sequence of remainders (including the final quotient of one) forms the binary value, as each remainder must be either zero or one when dividing by two. For example, (357)10 is expressed as (101100101)2.
Binary to decimal
Conversion from base-2 to base-10 simply inverts the preceding algorithm. The bits of the binary number are used one by one, starting with the most significant (leftmost) bit. Beginning with the value 0, the prior value is doubled, and the next bit is then added to produce the next value. This can be organized in a multi-column table. For example, to convert 100101011012 to decimal: The result is 119710. The first Prior Value of 0 is simply an initial decimal value. This method is an application of the Horner scheme. The fractional parts of a number are converted with similar methods. They are again based on the equivalence of shifting with doubling or halving. In a fractional binary number such as 0.110101101012, the first digit is , the second , etc. So if there is a 1 in the first place after the decimal, then the number is at least , and vice versa. Double that number is at least 1. This suggests the algorithm: Repeatedly double the number to be converted, record if the result is at least 1, and then throw away the integer part. For example, , in binary, is: Thus the repeating decimal fraction 0.... is equivalent to the repeating binary fraction 0.... . Or for example, 0.110, in binary, is: This is also a repeating binary fraction 0.0... . It may come as a surprise that terminating decimal fractions can have repeating expansions in binary. It is for this reason that many are surprised to discover that 1/10 + ... + 1/10 (addition of 10 numbers) differs from 1 in binaryfloating-point arithmetic
In computing, floating-point arithmetic (FP) is arithmetic on subsets of real numbers formed by a ''significand'' (a Sign (mathematics), signed sequence of a fixed number of digits in some Radix, base) multiplied by an integer power of that ba ...
. In fact, the only binary fractions with terminating expansions are of the form of an integer divided by a power of 2, which 1/10 is not.
The final conversion is from binary to decimal fractions. The only difficulty arises with repeating fractions, but otherwise the method is to shift the fraction to an integer, convert it as above, and then divide by the appropriate power of two in the decimal base. For example:
Another way of converting from binary to decimal, often quicker for a person familiar with hexadecimal
Hexadecimal (also known as base-16 or simply hex) is a Numeral system#Positional systems in detail, positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbo ...
, is to do so indirectly—first converting ( in binary) into ( in hexadecimal) and then converting ( in hexadecimal) into ( in decimal).
For very large numbers, these simple methods are inefficient because they perform a large number of multiplications or divisions where one operand is very large. A simple divide-and-conquer algorithm is more effective asymptotically: given a binary number, it is divided by 10''k'', where ''k'' is chosen so that the quotient roughly equals the remainder; then each of these pieces is converted to decimal and the two are concatenated. Given a decimal number, it can be split into two pieces of about the same size, each of which is converted to binary, whereupon the first converted piece is multiplied by 10''k'' and added to the second converted piece, where ''k'' is the number of decimal digits in the second, least-significant piece before conversion.
Hexadecimal
Binary may be converted to and from hexadecimal more easily. This is because theradix
In a positional numeral system, the radix (radices) or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, becaus ...
of the hexadecimal system (16) is a power of the radix of the binary system (2). More specifically, 16 = 24, so it takes four digits of binary to represent one digit of hexadecimal, as shown in the adjacent table.
To convert a hexadecimal number into its binary equivalent, simply substitute the corresponding binary digits:
:3A16 = 0011 10102
:E716 = 1110 01112
To convert a binary number into its hexadecimal equivalent, divide it into groups of four bits. If the number of bits isn't a multiple of four, simply insert extra 0 bits at the left (called padding). For example:
:10100102 = 0101 0010 grouped with padding = 5216
:110111012 = 1101 1101 grouped = DD16
To convert a hexadecimal number into its decimal equivalent, multiply the decimal equivalent of each hexadecimal digit by the corresponding power of 16 and add the resulting values:
:C0E716 = (12 × 163) + (0 × 162) + (14 × 161) + (7 × 160) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,38310
Octal
Binary is also easily converted to theoctal
Octal (base 8) is a numeral system with eight as the base.
In the decimal system, each place is a power of ten. For example:
: \mathbf_ = \mathbf \times 10^1 + \mathbf \times 10^0
In the octal system, each place is a power of eight. For ex ...
numeral system, since octal uses a radix of 8, which is a power of two (namely, 23, so it takes exactly three binary digits to represent an octal digit). The correspondence between octal and binary numerals is the same as for the first eight digits of hexadecimal
Hexadecimal (also known as base-16 or simply hex) is a Numeral system#Positional systems in detail, positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbo ...
in the table above. Binary 000 is equivalent to the octal digit 0, binary 111 is equivalent to octal 7, and so forth.
Converting from octal to binary proceeds in the same fashion as it does for hexadecimal
Hexadecimal (also known as base-16 or simply hex) is a Numeral system#Positional systems in detail, positional numeral system that represents numbers using a radix (base) of sixteen. Unlike the decimal system representing numbers using ten symbo ...
:
:658 = 110 1012
:178 = 001 1112
And from binary to octal:
:1011002 = 101 1002 grouped = 548
:100112 = 010 0112 grouped with padding = 238
And from octal to decimal:
:658 = (6 × 81) + (5 × 80) = (6 × 8) + (5 × 1) = 5310
:1278 = (1 × 82) + (2 × 81) + (7 × 80) = (1 × 64) + (2 × 8) + (7 × 1) = 8710
Representing real numbers
Non-integers can be represented by using negative powers, which are set off from the other digits by means of a radix point (called a decimal point in the decimal system). For example, the binary number 11.012 means: For a total of 3.25 decimal. All dyadic rational numbers have a ''terminating'' binary numeral—the binary representation has a finite number of terms after the radix point. Otherrational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction (mathematics), fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for examp ...
have binary representation, but instead of terminating, they ''recur'', with a finite sequence of digits repeating indefinitely. For instance
The phenomenon that the binary representation of any rational is either terminating or recurring also occurs in other radix-based numeral systems. See, for instance, the explanation in decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
. Another similarity is the existence of alternative representations for any terminating representation, relying on the fact that 0.111111... is the sum of the geometric series 2−1 + 2−2 + 2−3 + ... which is 1.
Binary numerals that neither terminate nor recur represent irrational number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, ...
s. For instance,
* 0.10100100010000100000100... does have a pattern, but it is not a fixed-length recurring pattern, so the number is irrational
* 1.0110101000001001111001100110011111110... is the binary representation of , the square root of 2
The square root of 2 (approximately 1.4142) is the positive real number that, when multiplied by itself or squared, equals the number 2. It may be written as \sqrt or 2^. It is an algebraic number, and therefore not a transcendental number. Te ...
, another irrational. It has no discernible pattern.
See also
*ASCII
ASCII ( ), an acronym for American Standard Code for Information Interchange, is a character encoding standard for representing a particular set of 95 (English language focused) printable character, printable and 33 control character, control c ...
* Balanced ternary
* Bitwise operation
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operatio ...
* Binary code
A binary code represents plain text, text, instruction set, computer processor instructions, or any other data using a two-symbol system. The two-symbol system used is often "0" and "1" from the binary number, binary number system. The binary cod ...
* Binary-coded decimal
* Finger binary
* Gray code
The reflected binary code (RBC), also known as reflected binary (RB) or Gray code after Frank Gray (researcher), Frank Gray, is an ordering of the binary numeral system such that two successive values differ in only one bit (binary digit).
For ...
* IEEE 754
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic originally established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard #Design rationale, add ...
* Linear-feedback shift register
* Offset binary
* Quibinary
* Reduction of summands
* Redundant binary representation
* Repeating decimal
A repeating decimal or recurring decimal is a decimal representation of a number whose digits are eventually periodic (that is, after some place, the same sequence of digits is repeated forever); if this sequence consists only of zeros (that i ...
* Two's complement
* Unicode
Unicode or ''The Unicode Standard'' or TUS is a character encoding standard maintained by the Unicode Consortium designed to support the use of text in all of the world's writing systems that can be digitized. Version 16.0 defines 154,998 Char ...
References
External links
Binary System
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
Conversion of Fractions
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
* Sir Francis Bacon's BiLiteral Cypher system , predates binary number system.
{{Authority control
Binary arithmetic
Computer arithmetic
Elementary arithmetic
Gottfried Wilhelm Leibniz
Power-of-two numeral systems