Beltrami–Klein Model on:
[Wikipedia]
[Google]
[Amazon]

 In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of
 While lines in the hyperbolic plane are straightforward to project into the Klein disk model, circles, hypercycles and horocycles are not.
Circles in the model that are not
While lines in the hyperbolic plane are straightforward to project into the Klein disk model, circles, hypercycles and horocycles are not.
Circles in the model that are not
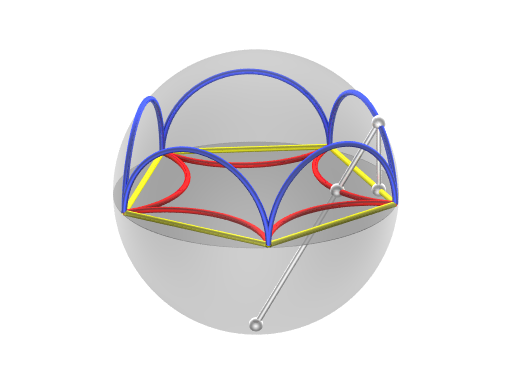
 Both the
Both the
 Given two distinct points ''U'' and ''V'' in the open unit ball of the model in
Given two distinct points ''U'' and ''V'' in the open unit ball of the model in answer
from Stack Exchange :
 The
The
 In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of
In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
in which points are represented by the points in the interior of the unit disk
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1:
:D_1(P) = \.\,
The closed unit disk around ''P'' is the set of points whose d ...
(or ''n''-dimensional unit ball
Unit may refer to:
General measurement
* Unit of measurement, a definite magnitude of a physical quantity, defined and adopted by convention or by law
**International System of Units (SI), modern form of the metric system
**English units, histo ...
) and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
.
It is analogous to the gnomonic projection of spherical geometry
300px, A sphere with a spherical triangle on it.
Spherical geometry or spherics () is the geometry of the two-dimensional surface of a sphere or the -dimensional surface of higher dimensional spheres.
Long studied for its practical applicati ...
, in that geodesics
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connec ...
(great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
s in spherical geometry) are mapped to straight lines.
This model is not conformal: angles are not faithfully represented, and circles become ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
s, increasingly flattened near the edge. This is in contrast to the Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
, which is conformal. However, lines in the Poincaré model are not represented by straight line segments, but by arcs that meet the boundary orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
ly.
The Beltrami–Klein model is named after the Italian geometer Eugenio Beltrami and the German Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
while "Cayley" in Cayley–Klein model refers to the English geometer Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
.
History
This model made its first appearance forhyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or János Bolyai, Bolyai–Nikolai Lobachevsky, Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For a ...
in two memoirs of Eugenio Beltrami published in 1868, first for dimension and then for general ''n'', and these essays proved the equiconsistency
In mathematical logic, two theory (mathematical logic), theories are equiconsistent if the consistency of one theory implies the consistency of the other theory, and Vice-versa, vice versa. In this case, they are, roughly speaking, "as consistent ...
of hyperbolic geometry with ordinary Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
.
The papers of Beltrami remained little noticed until recently and the model was named after Klein ("The Klein disk model"). In 1859 Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
used the cross-ratio
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points , , , on a line, their cross ratio is defin ...
definition of angle due to Laguerre to show how Euclidean geometry could be defined using projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
. His definition of distance later became known as the Cayley metric.
In 1869, the young (twenty-year-old) Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
became acquainted with Cayley's work. He recalled that in 1870 he gave a talk on the work of Cayley at the seminar of Weierstrass
Karl Theodor Wilhelm Weierstrass (; ; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the " father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school t ...
and he wrote:
:"I finished with a question whether there might exist a connection between the ideas of Cayley and Lobachevsky. I was given the answer that these two systems were conceptually widely separated."
Later, Felix Klein
Felix Christian Klein (; ; 25 April 1849 – 22 June 1925) was a German mathematician and Mathematics education, mathematics educator, known for his work in group theory, complex analysis, non-Euclidean geometry, and the associations betwe ...
realized that Cayley's ideas give rise to a projective model of the non-Euclidean plane.
As Klein puts it, "I allowed myself to be convinced by these objections and put aside this already mature idea." However, in 1871, he returned to this idea, formulated it mathematically, and published it.
Distance formula
The distance function for the Beltrami–Klein model is a Cayley–Klein metric. Given two distinct points ''p'' and ''q'' in the open unit ball, the unique straight line connecting them intersects the boundary at two ideal points, ''a'' and ''b'', label them so that the points are, in order, ''a'', ''p'', ''q'', ''b'', so that and . The hyperbolic distance between ''p'' and ''q'' is then: The vertical bars indicate Euclidean distances between the points in the model, where ln is thenatural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
and the factor of one half is needed to give the model the standard curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
of −1.
When one of the points is the origin and Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
between the points is ''r'' then the hyperbolic distance is:
:
where '' artanh'' is the inverse hyperbolic function
In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangen ...
of the hyperbolic tangent.
The Klein disk model
In two dimensions the Beltrami–Klein model is called the Klein disk model. It is a disk and the inside of the disk is a model of the entire hyperbolic plane. Lines in this model are represented by chords of the boundary circle (also called the ''absolute
Absolute may refer to:
Companies
* Absolute Entertainment, a video game publisher
* Absolute Radio, (formerly Virgin Radio), independent national radio station in the UK
* Absolute Software Corporation, specializes in security and data risk ma ...
'').
The points on the boundary circle are called ideal points;
although well defined, they do not belong to the hyperbolic plane.
Points outside the disk do not belong to the hyperbolic plane either, and they are sometimes called ultra ideal points.
The model is not conformal, meaning that angles
are distorted, and circles on the hyperbolic plane are in general not circular in the model.
Only circles that have their centre at the centre of the boundary circle are not distorted. All other circles are distorted, as are horocycles and hypercycles.
Properties
Chords that meet on the boundary circle are limiting parallel lines. Two chords are perpendicular if, when extended outside the disk, each goes through the pole of the other. (The pole of a chord is an ultra ideal point: the point outside the disk where the tangents to the disk at the endpoints of the chord meet.) Chords that go through the centre of the disk have their pole at infinity, orthogonal to the direction of the chord (this implies that right angles on diameters are not distorted).Compass and straightedge constructions
Here is how one can usecompass and straightedge constructions
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
in the model to achieve the effect of the basic constructions in the hyperbolic plane.
* The pole of a line. While the pole is not a point in the hyperbolic plane (it is an ultra ideal point) most constructions will use the pole of a line in one or more ways.
:For a line: construct the tangents to the boundary circle through the ideal (end) points of the line. the point where these tangents intersect is the pole.
:For diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
s of the disk: the pole is at infinity perpendicular to the diameter.
*To construct a perpendicular to a given line through a given point, draw the ray from the pole of the line through the given point. The part of the ray that is inside the disk is the perpendicular.
: When the line is a diameter of the disk then the perpendicular is the chord that is (Euclidean) perpendicular to that diameter and going through the given point.
* To find the midpoint of given segment : Draw the lines through A and B that are perpendicular to . (see above) Draw the lines connecting the ideal points of these lines, two of these lines will intersect the segment and will do this at the same point. This point is the (hyperbolic) midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dim ...
of.
* To bisect a given angle : Draw the rays AB and AC. Draw tangents to the circle where the rays intersect the boundary circle. Draw a line from ''A'' to the point where the tangents intersect. The part of this line between ''A'' and the boundary circle is the bisector.
* The common perpendicular of two lines is the chord that when extended goes through both poles
Pole or poles may refer to:
People
*Poles (people), another term for Polish people, from the country of Poland
* Pole (surname), including a list of people with the name
* Pole (musician) (Stefan Betke, born 1967), German electronic music artist
...
of the chords.
: When one of the chords is a diameter of the boundary circle then the common perpendicular is the chord that is perpendicular to the diameter and that when lengthened goes through the pole of the other chord.
*To reflect a point P in a line l: From a point R on the line l draw the ray through P. Let X be the ideal point where the ray intersects the absolute. Draw the ray from the pole of line l through X, let Y be another ideal point that intersects the ray. Draw the segment RY. The reflection of point P is the point where the ray from the pole of line l through P intersects RY.
Circles, hypercycles and horocycles
concentric
In geometry, two or more objects are said to be ''concentric'' when they share the same center. Any pair of (possibly unalike) objects with well-defined centers can be concentric, including circles, spheres, regular polygons, regular polyh ...
with the model become ellipses, increasing in eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
near the edge. Angles, hypercycles, and horocycles in the Klein disk model are also deformed.
For constructions in the hyperbolic plane that contain circles, hypercycles, horocycles or non right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
s it is perhaps more convenient to use the Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
or the Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically, each point in the hyperbolic plane is represented using a Euclidean point with co ...
.
Relation to the Poincaré disk model

 Both the
Both the Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
and the Klein disk model are models of the hyperbolic plane. An advantage of the Poincaré disk model is that it is conformal (circles and angles are not distorted); a disadvantage is that straight lines project to circular arc
A circular arc is the arc of a circle between a pair of distinct points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the center of the circle that is less than radians (180 ...
s orthogonal to the boundary circle of the disk.
The two models are related through a projection on or from the hemisphere model. The Klein model is an orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in ...
to the hemisphere model, while the Poincaré disk model is a stereographic projection
In mathematics, a stereographic projection is a perspective transform, perspective projection of the sphere, through a specific point (geometry), point on the sphere (the ''pole'' or ''center of projection''), onto a plane (geometry), plane (th ...
.
Straight lines always intersect the circular boundary of the two models in the same place, regardless of which model is used. Also, the pole of the chord is the centre of the circle that contains the arc.
If P is a point a distance from the centre of the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
in the Beltrami–Klein model, then the corresponding point on the Poincaré disk model a distance of u on the same radius:
:
Conversely, If P is a point a distance from the centre of the unit circle in the Poincaré disk model, then the corresponding point of the Beltrami–Klein model is a distance of s on the same radius:
:
Relation of the disk model to the hyperboloid model and the gnomonic projection of the sphere
The gnomonic projection of the sphere projects from the sphere's center onto a tangent plane. Every great circle on the sphere is projected to a straight line, but it is not conformal. Angles are not faithfully represented, and circles become ellipses, increasingly stretched as they get further from the tangent point. Similarly the Klein disk (K, in the picture) is a gnomonic projection of the hyperboloid model (Hy) with as center the center of the hyperboloid (O) and the projection plane tangent to the hyperboloid.Distance and metric tensor
 Given two distinct points ''U'' and ''V'' in the open unit ball of the model in
Given two distinct points ''U'' and ''V'' in the open unit ball of the model in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, the unique straight line connecting them intersects the unit sphere at two ideal points ''A'' and ''B'', labeled so that the points are, in order along the line, ''A'', ''U'', ''V'', ''B''. Taking the centre of the unit ball of the model as the origin, and assigning position vectors u, v, a, b respectively to the points ''U'', ''V'', ''A'', ''B'', we have that that and , where denotes the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' ...
. Then the distance between ''U'' and ''V'' in the modelled hyperbolic space is expressed as
:
where the factor of one half is needed to make the curvature
In mathematics, curvature is any of several strongly related concepts in geometry that intuitively measure the amount by which a curve deviates from being a straight line or by which a surface deviates from being a plane. If a curve or su ...
−1.
The associated metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
is given byfrom Stack Exchange :
Relation to the hyperboloid model
 The
The hyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperboloi ...
is a model of hyperbolic geometry within -dimensional Minkowski space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a ...
. The Minkowski inner product is given by
:
and the norm by . The hyperbolic plane is embedded in this space as the vectors x with and ''x''0 (the "timelike component") positive. The intrinsic distance (in the embedding) between points u and v is then given by
:
This may also be written in the homogeneous form
:
which allows the vectors to be rescaled for convenience.
The Beltrami–Klein model is obtained from the hyperboloid model by rescaling all vectors so that the timelike component is 1, that is, by projecting the hyperboloid embedding through the origin onto the plane . The distance function, in its homogeneous form, is unchanged. Since the intrinsic lines (geodesics) of the hyperboloid model are the intersection of the embedding with planes through the Minkowski origin, the intrinsic lines of the Beltrami–Klein model are the chords of the sphere.
Relation to the Poincaré ball model
Both the Poincaré ball model and the Beltrami–Klein model are models of the ''n''-dimensional hyperbolic space in the ''n''-dimensional unit ball in R''n''. If is a vector of norm less than one representing a point of the Poincaré disk model, then the corresponding point of the Beltrami–Klein model is given by : Conversely, from a vector of norm less than one representing a point of the Beltrami–Klein model, the corresponding point of the Poincaré disk model is given by : Given two points on the boundary of the unit disk, which are called ''ideal points'', the straight line connecting them in the Beltrami–Klein model is the chord between them, while in the corresponding Poincaré model the line is acircular arc
A circular arc is the arc of a circle between a pair of distinct points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the center of the circle that is less than radians (180 ...
on the two-dimensional subspace generated by the two boundary point vectors, meeting the boundary of the ball at right angles. The two models are related through a projection from the center of the disk; a ray from the center passing through a point of one model line passes through the corresponding point of the line in the other model.
See also
*Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically, each point in the hyperbolic plane is represented using a Euclidean point with co ...
*Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
* Poincaré metric
*Inversive geometry
In geometry, inversive geometry is the study of ''inversion'', a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry ...
Notes
References
*Luis Santaló (1961), '' Geometrias no Euclidianas, EUDEBA. * * {{DEFAULTSORT:Beltrami-Klein model Hyperbolic geometry