Arithmetic Rope on:
[Wikipedia]
[Google]
[Amazon]
 Arithmetic is an elementary branch of
Arithmetic is an elementary branch of
 The main kinds of numbers employed in arithmetic are
The main kinds of numbers employed in arithmetic are 

 Integer arithmetic is the branch of arithmetic that deals with the manipulation of positive and negative whole numbers. Simple one-digit operations can be performed by following or memorizing a table that presents the results of all possible combinations, like an
Integer arithmetic is the branch of arithmetic that deals with the manipulation of positive and negative whole numbers. Simple one-digit operations can be performed by following or memorizing a table that presents the results of all possible combinations, like an
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
that deals with numerical operations like addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that repre ...
, multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, and division. In a wider sense, it also includes exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, extraction of roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusin ...
, and taking logarithms
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
.
Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s. Rational number arithmetic involves operations on fraction
A fraction (from , "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, thre ...
s of integers. Real number arithmetic is about calculations with real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s, which include both rational
Rationality is the quality of being guided by or based on reason. In this regard, a person acts rationally if they have a good reason for what they do, or a belief is rational if it is based on strong evidence. This quality can apply to an ...
and irrational number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, ...
s.
Another distinction is based on the numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
employed to perform calculations. Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of th ...
arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express number
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
s. Binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two values (0 and 1) for each digit
* Binary function, a function that takes two arguments
* Binary operation, a mathematical op ...
arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Computer arithmetic
Computer arithmetic is the scientific field that deals with representation of numbers on computers and corresponding implementations of the arithmetic operations.
It includes:
*Fixed-point arithmetic
*Floating-point arithmetic
*Interval arithmet ...
deals with the specificities of the implementation of binary arithmetic on computer
A computer is a machine that can be Computer programming, programmed to automatically Execution (computing), carry out sequences of arithmetic or logical operations (''computation''). Modern digital electronic computers can perform generic set ...
s. Some arithmetic systems operate on mathematical object
A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a Glossary of mathematical symbols, symbol, and therefore can be involved in formulas. Commonly encounter ...
s other than numbers, such as interval arithmetic
Interval arithmetic (also known as interval mathematics; interval analysis or interval computation) is a mathematical technique used to mitigate rounding and measurement errors in mathematical computation by computing function bounds. Numeri ...
and matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
arithmetic.
Arithmetic operations form the basis of many branches of mathematics, such as algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, and statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
. They play a similar role in the sciences
Science is a systematic discipline that builds and organises knowledge in the form of testable hypotheses and predictions about the universe. Modern science is typically divided into twoor threemajor branches: the natural sciences, which stu ...
, like physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
and economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
. Arithmetic is present in many aspects of daily life
Everyday life, daily life or routine life comprises the ways in which people typically act, think, and feel on a daily basis. Everyday life may be described as mundane, routine, natural, habitual, or normal.
Human diurnality means most peop ...
, for example, to calculate change while shopping or to manage personal finances
Personal finance is the financial management that an individual or a family unit performs to budget, save, and spend monetary resources in a controlled manner, taking into account various financial risks and future life events.
When planning ...
. It is one of the earliest forms of mathematics education
In contemporary education, mathematics education—known in Europe as the didactics or pedagogy of mathematics—is the practice of teaching, learning, and carrying out Scholarly method, scholarly research into the transfer of mathematical know ...
that students encounter. Its cognitive and conceptual foundations are studied by psychology
Psychology is the scientific study of mind and behavior. Its subject matter includes the behavior of humans and nonhumans, both consciousness, conscious and Unconscious mind, unconscious phenomena, and mental processes such as thoughts, feel ...
and philosophy
Philosophy ('love of wisdom' in Ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, Value (ethics and social sciences), value, mind, and language. It is a rational an ...
.
The practice of arithmetic is at least thousands and possibly tens of thousands of years old. Ancient civilizations like the Egyptians
Egyptians (, ; , ; ) are an ethnic group native to the Nile, Nile Valley in Egypt. Egyptian identity is closely tied to Geography of Egypt, geography. The population is concentrated in the Nile Valley, a small strip of cultivable land stretchi ...
and the Sumer
Sumer () is the earliest known civilization, located in the historical region of southern Mesopotamia (now south-central Iraq), emerging during the Chalcolithic and Early Bronze Age, early Bronze Ages between the sixth and fifth millennium BC. ...
ians invented numeral systems to solve practical arithmetic problems in about 3000 BCE. Starting in the 7th and 6th centuries BCE, the ancient Greeks
Ancient Greece () was a northeastern Mediterranean civilization, existing from the Greek Dark Ages of the 12th–9th centuries BC to the end of classical antiquity (), that comprised a loose collection of culturally and linguistically re ...
initiated a more abstract study of numbers and introduced the method of rigorous mathematical proof
A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use othe ...
s. The ancient India
Anatomically modern humans first arrived on the Indian subcontinent between 73,000 and 55,000 years ago. The earliest known human remains in South Asia date to 30,000 years ago. Sedentism, Sedentariness began in South Asia around 7000 BCE; ...
ns developed the concept of zero
0 (zero) is a number representing an empty quantity. Adding (or subtracting) 0 to any number leaves that number unchanged; in mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and compl ...
and the decimal system, which Arab mathematicians further refined and spread to the Western world during the medieval period. The first mechanical calculator
A mechanical calculator, or calculating machine, is a mechanical device used to perform the basic operations of arithmetic automatically, or a simulation like an analog computer or a slide rule. Most mechanical calculators were comparable in si ...
s were invented in the 17th century. The 18th and 19th centuries saw the development of modern number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
and the formulation of axiomatic foundations of arithmetic. In the 20th century, the emergence of electronic calculator
An electronic calculator is typically a portable Electronics, electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics.
The first solid-state electronic calculator was created in the early 1960s. ...
s and computers revolutionized the accuracy and speed with which arithmetic calculations could be performed.
Definition, etymology, and related fields
Arithmetic is the fundamental branch ofmathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
that studies numbers and their operations. In particular, it deals with numerical calculations using the arithmetic operations of addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that repre ...
, multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, and division. In a wider sense, it also includes exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, extraction of roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusin ...
, and logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
. The term ''arithmetic'' has its root in the Latin term which derives from the Ancient Greek words (''arithmos''), meaning , and (''arithmetike tekhne''), meaning .
There are disagreements about its precise definition. According to a narrow characterization, arithmetic deals only with natural numbers
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positiv ...
. However, the more common view is to include operations on integers
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction (mathematics), fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for examp ...
, real numbers
In mathematics, a real number is a number that can be used to measurement, measure a continuous variable, continuous one-dimensional quantity such as a time, duration or temperature. Here, ''continuous'' means that pairs of values can have arbi ...
, and sometimes also complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
in its scope. Some definitions restrict arithmetic to the field of numerical calculations. When understood in a wider sense, it also includes the study of how the concept of numbers
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
developed, the analysis of properties of and relations between numbers, and the examination of the axiomatic structure of arithmetic operations.
Arithmetic is closely related to number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
and some authors use the terms as synonyms. However, in a more specific sense, number theory is restricted to the study of integers and focuses on their properties and relationships such as divisibility
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a ''Multiple (mathematics), multiple'' of m. An integer n is divis ...
, factorization
In mathematics, factorization (or factorisation, see American and British English spelling differences#-ise, -ize (-isation, -ization), English spelling differences) or factoring consists of writing a number or another mathematical object as a p ...
, and primality
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. Traditionally, it is known as higher arithmetic.
Numbers
Number
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can ...
s are mathematical object
A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a Glossary of mathematical symbols, symbol, and therefore can be involved in formulas. Commonly encounter ...
s used to count quantities and measure magnitudes. They are fundamental elements in arithmetic since all arithmetic operations are performed on numbers. There are different kinds of numbers and different numeral systems
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent different ...
to represent them.
Kinds
 The main kinds of numbers employed in arithmetic are
The main kinds of numbers employed in arithmetic are natural numbers
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positiv ...
, whole numbers, integers
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction (mathematics), fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for examp ...
, and real numbers
In mathematics, a real number is a number that can be used to measurement, measure a continuous variable, continuous one-dimensional quantity such as a time, duration or temperature. Here, ''continuous'' means that pairs of values can have arbi ...
. The natural numbers are whole numbers that start from 1 and go to infinity. They exclude 0 and negative numbers. They are also known as counting numbers and can be expressed as . The symbol of the natural numbers is . The whole numbers are identical to the natural numbers with the only difference being that they include 0. They can be represented as and have the symbol . Some mathematicians do not draw the distinction between the natural and the whole numbers by including 0 in the set of natural numbers. The set of integers encompasses both positive and negative whole numbers. It has the symbol and can be expressed as .
Based on how natural and whole numbers are used, they can be distinguished into cardinal
Cardinal or The Cardinal most commonly refers to
* Cardinalidae, a family of North and South American birds
**''Cardinalis'', genus of three species in the family Cardinalidae
***Northern cardinal, ''Cardinalis cardinalis'', the common cardinal of ...
and ordinal number
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals (first, second, th, etc.) aimed to extend enumeration to infinite sets.
A finite set can be enumerated by successively labeling each element with the leas ...
s. Cardinal numbers, like one, two, and three, are numbers that express the quantity of objects. They answer the question "how many?". Ordinal numbers, such as first, second, and third, indicate order or placement in a series. They answer the question "what position?".
A number is rational if it can be represented as the ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of two integers. For instance, the rational number is formed by dividing the integer 1, called the numerator, by the integer 2, called the denominator. Other examples are and . The set of rational numbers includes all integers, which are fraction
A fraction (from , "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, thre ...
s with a denominator of 1. The symbol of the rational numbers is . Decimal fraction
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers (''decimal fractions'') of the ...
s like 0.3 and 25.12 are a special type of rational numbers since their denominator is a power of 10. For instance, 0.3 is equal to , and 25.12 is equal to . Every rational number corresponds to a finite or a repeating decimal
A repeating decimal or recurring decimal is a decimal representation of a number whose digits are eventually periodic (that is, after some place, the same sequence of digits is repeated forever); if this sequence consists only of zeros (that i ...
.
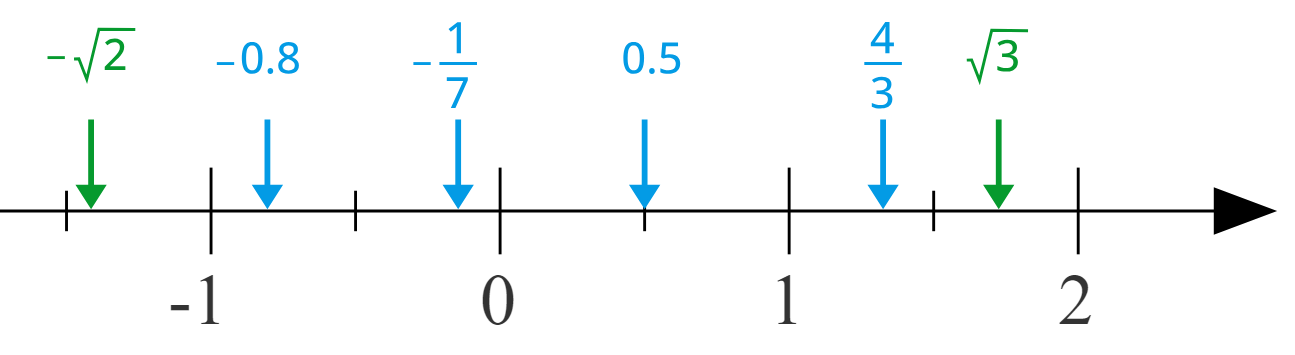
Irrational numbers
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, ...
are numbers that cannot be expressed through the ratio of two integers. They are often required to describe geometric magnitudes. For example, if a right triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees).
The side opposite to the right angle i ...
has legs of the length 1 then the length of its hypotenuse
In geometry, a hypotenuse is the side of a right triangle opposite to the right angle. It is the longest side of any such triangle; the two other shorter sides of such a triangle are called '' catheti'' or ''legs''. Every rectangle can be divided ...
is given by the irrational number . is another irrational number and describes the ratio of a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
's circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
to its diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
. The decimal representation of an irrational number is infinite without repeating decimals. The set of rational numbers together with the set of irrational numbers makes up the set of real numbers. The symbol of the real numbers is . Even wider classes of numbers include complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a ...
and quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s.
Numeral systems
A numeral is a symbol to represent a number and numeral systems are representational frameworks. They usually have a limited amount of basic numerals, which directly refer to certain numbers. The system governs how these basic numerals may be combined to express any number. Numeral systems are either positional or non-positional. All early numeral systems were non-positional. For non-positional numeral systems, the value of a digit does not depend on its position in the numeral. The simplest non-positional system is theunary numeral system
The unary numeral system is the simplest numeral system to represent natural numbers: to represent a number ''N'', a symbol representing 1 is repeated ''N'' times.
In the unary system, the number 0 (zero) is represented by the empty string, tha ...
. It relies on one symbol for the number 1. All higher numbers are written by repeating this symbol. For example, the number 7 can be represented by repeating the symbol for 1 seven times. This system makes it cumbersome to write large numbers, which is why many non-positional systems include additional symbols to directly represent larger numbers. Variations of the unary numeral systems are employed in tally stick
A tally stick (or simply a tally) was an ancient memory aid used to record and document numbers, quantities, and messages. Tally sticks first appear as animal bones carved with notches during the Upper Palaeolithic; a notable example is the Is ...
s using dents and in tally marks
Tally marks, also called hash marks, are a form of numeral used for counting. They can be thought of as a unary numeral system.
They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no inter ...
.
Egyptian hieroglyphics
Ancient Egyptian hieroglyphs ( ) were the formal writing system used in Ancient Egypt for writing the Egyptian language. Hieroglyphs combined ideographic, logographic, syllabic and alphabetic elements, with more than 1,000 distinct characters.I ...
had a more complex non-positional numeral system
A numeral system is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbols may represent differe ...
. They have additional symbols for numbers like 10, 100, 1000, and 10,000. These symbols can be combined into a sum to more conveniently express larger numbers. For instance, the numeral for 10,405 uses one time the symbol for 10,000, four times the symbol for 100, and five times the symbol for 1. A similar well-known framework is the Roman numeral system. It has the symbols I, V, X, L, C, D, M as its basic numerals to represent the numbers 1, 5, 10, 50, 100, 500, and 1000.
A numeral system is positional if the position of a basic numeral in a compound expression determines its value. Positional numeral systems have a radix
In a positional numeral system, the radix (radices) or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, becaus ...
that acts as a multiplicand of the different positions. For each subsequent position, the radix is raised to a higher power. In the common decimal system, also called the Hindu–Arabic numeral system
The Hindu–Arabic numeral system (also known as the Indo-Arabic numeral system, Hindu numeral system, and Arabic numeral system) is a positional notation, positional Decimal, base-ten numeral system for representing integers; its extension t ...
, the radix is 10. This means that the first digit is multiplied by , the next digit is multiplied by , and so on. For example, the decimal numeral 532 stands for . Because of the effect of the digits' positions, the numeral 532 differs from the numerals 325 and 253 even though they have the same digits.
Another positional numeral system used extensively in computer arithmetic
Computer arithmetic is the scientific field that deals with representation of numbers on computers and corresponding implementations of the arithmetic operations.
It includes:
*Fixed-point arithmetic
*Floating-point arithmetic
*Interval arithmet ...
is the binary system
A binary system is a system of two astronomical bodies of the same kind that are comparable in size. Definitions vary, but typically require the center of mass to be located outside of either object. (See animated examples.)
The most common ki ...
, which has a radix of 2. This means that the first digit is multiplied by , the next digit by , and so on. For example, the number 13 is written as 1101 in the binary notation, which stands for . In computing, each digit in the binary notation corresponds to one bit
The bit is the most basic unit of information in computing and digital communication. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented as ...
. The earliest positional system was developed by ancient Babylonians and had a radix of 60.
Operations
Arithmetic operations are ways of combining, transforming, or manipulating numbers. They are functions that have numbers both as input and output. The most important operations in arithmetic areaddition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that repre ...
, multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, and division. Further operations include exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, extraction of roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusin ...
, and logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
. If these operations are performed on variables rather than numbers, they are sometimes referred to as algebraic operations.
Two important concepts in relation to arithmetic operations are identity element
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
s and inverse element
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
s. The identity element or neutral element of an operation does not cause any change if it is applied to another element. For example, the identity element of addition is 0 since any sum of a number and 0 results in the same number. The inverse element is the element that results in the identity element when combined with another element. For instance, the additive inverse
In mathematics, the additive inverse of an element , denoted , is the element that when added to , yields the additive identity, 0 (zero). In the most familiar cases, this is the number 0, but it can also refer to a more generalized zero el ...
of the number 6 is -6 since their sum is 0.
There are not only inverse elements but also inverse operations. In an informal sense, one operation is the inverse of another operation if it undoes the first operation. For example, subtraction is the inverse of addition since a number returns to its original value if a second number is first added and subsequently subtracted, as in . Defined more formally, the operation "" is an inverse of the operation "" if it fulfills the following condition: if and only if .
Commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
and associativity
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replaceme ...
are laws governing the order in which some arithmetic operations can be carried out. An operation is commutative if the order of the arguments can be changed without affecting the results. This is the case for addition, for instance, is the same as . Associativity is a rule that affects the order in which a series of operations can be carried out. An operation is associative if, in a series of two operations, it does not matter which operation is carried out first. This is the case for multiplication, for example, since is the same as .
Addition and subtraction
Addition is an arithmetic operation in which two numbers, called the addends, are combined into a single number, called the sum. The symbol of addition is . Examples are and . The termsummation
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, pol ...
is used if several additions are performed in a row. Counting is a type of repeated addition in which the number 1 is continuously added.
Subtraction is the inverse of addition. In it, one number, known as the subtrahend, is taken away from another, known as the minuend. The result of this operation is called the difference. The symbol of subtraction is . Examples are and . Subtraction is often treated as a special case of addition: instead of subtracting a positive number, it is also possible to add a negative number. For instance . This helps to simplify mathematical computations by reducing the number of basic arithmetic operations needed to perform calculations.
The additive identity element is 0 and the additive inverse of a number is the negative of that number. For instance, and . Addition is both commutative and associative.
Multiplication and division
Multiplication is an arithmetic operation in which two numbers, called the multiplier and the multiplicand, are combined into a single number called the product. The symbols of multiplication are , , and *. Examples are and . If the multiplicand is a natural number then multiplication is the same as repeated addition, as in . Division is the inverse of multiplication. In it, one number, known as the dividend, is split into several equal parts by another number, known as the divisor. The result of this operation is called thequotient
In arithmetic, a quotient (from 'how many times', pronounced ) is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics. It has two definitions: either the integer part of a division (in th ...
. The symbols of division are and . Examples are and . Division is often treated as a special case of multiplication: instead of dividing by a number, it is also possible to multiply by its reciprocal. The reciprocal of a number is 1 divided by that number. For instance, .
The multiplicative identity
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
element is 1 and the multiplicative inverse of a number is the reciprocal of that number. For example, and . Multiplication is both commutative and associative.
Exponentiation and logarithm
Exponentiation is an arithmetic operation in which a number, known as the base, is raised to the power of another number, known as the exponent. The result of this operation is called the power. Exponentiation is sometimes expressed using the symbol ^ but the more common way is to write the exponent insuperscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, wh ...
right after the base. Examples are and ^. If the exponent is a natural number then exponentiation is the same as repeated multiplication, as in .
Roots are a special type of exponentiation using a fractional exponent. For example, the square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
of a number is the same as raising the number to the power of and the cube root
In mathematics, a cube root of a number is a number that has the given number as its third power; that is y^3=x. The number of cube roots of a number depends on the number system that is considered.
Every real number has exactly one real cub ...
of a number is the same as raising the number to the power of . Examples are and .
Logarithm is the inverse of exponentiation. The logarithm of a number to the base is the exponent
In mathematics, exponentiation, denoted , is an operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, i ...
to which must be raised to produce . For instance, since , the logarithm base 10 of 1000 is 3. The logarithm of to base is denoted as , or without parentheses, , or even without the explicit base, , when the base can be understood from context. So, the previous example can be written .
Exponentiation and logarithm do not have general identity elements and inverse elements like addition and multiplication. The neutral element of exponentiation in relation to the exponent is 1, as in . However, exponentiation does not have a general identity element since 1 is not the neutral element for the base. Exponentiation and logarithm are neither commutative nor associative.
Types
Different types of arithmetic systems are discussed in the academic literature. They differ from each other based on what type of number they operate on, what numeral system they use to represent them, and whether they operate on mathematical objects other than numbers.Integer arithmetic
addition table
Addition (usually signified by the plus symbol, +) is one of the four basic operations of arithmetic, the other three being subtraction, multiplication, and division. The addition of two whole numbers results in the total or '' sum'' of th ...
or a multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication binary operation, operation for an algebraic system.
The decimal multiplication table was traditionally tau ...
. Other common methods are verbal counting
Counting is the process of determining the number of elements of a finite set of objects; that is, determining the size of a set. The traditional way of counting consists of continually increasing a (mental or spoken) counter by a unit for ever ...
and finger-counting
Finger-counting, also known as dactylonomy, is the act of counting using one's fingers. There are multiple different systems used across time and between cultures, though many of these have seen a decline in use because of the spread of Arabic nu ...
.
For operations on numbers with more than one digit, different techniques can be employed to calculate the result by using several one-digit operations in a row. For example, in the method addition with carries, the two numbers are written one above the other. Starting from the rightmost digit, each pair of digits is added together. The rightmost digit of the sum is written below them. If the sum is a two-digit number then the leftmost digit, called the "carry", is added to the next pair of digits to the left. This process is repeated until all digits have been added. Other methods used for integer additions are the number line
A number line is a graphical representation of a straight line that serves as spatial representation of numbers, usually graduated like a ruler with a particular origin point representing the number zero and evenly spaced marks in either dire ...
method, the partial sum method, and the compensation method. A similar technique is utilized for subtraction: it also starts with the rightmost digit and uses a "borrow" or a negative carry for the column on the left if the result of the one-digit subtraction is negative.
A basic technique of integer multiplication employs repeated addition. For example, the product of can be calculated as . A common technique for multiplication with larger numbers is called long multiplication. This method starts by writing the multiplier above the multiplicand. The calculation begins by multiplying the multiplier only with the rightmost digit of the multiplicand and writing the result below, starting in the rightmost column. The same is done for each digit of the multiplicand and the result in each case is shifted one position to the left. As a final step, all the individual products are added to arrive at the total product of the two multi-digit numbers. Other techniques used for multiplication are the grid method and the lattice method. Computer science is interested in multiplication algorithms with a low computational complexity
In computer science, the computational complexity or simply complexity of an algorithm is the amount of resources required to run it. Particular focus is given to computation time (generally measured by the number of needed elementary operations ...
to be able to efficiently multiply very large integers, such as the Karatsuba algorithm
The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962.
Knuth D.E. (1969) '' The Art of Computer Programming. v.2.'' Addison-Wesley Publ.Co., 724 pp ...
, the Schönhage–Strassen algorithm, and the Toom–Cook algorithm. A common technique used for division is called long division
In arithmetic, long division is a standard division algorithm suitable for dividing multi-digit Hindu-Arabic numerals (positional notation) that is simple enough to perform by hand. It breaks down a division problem into a series of easier step ...
. Other methods include short division and chunking.
Integer arithmetic is not closed under division. This means that when dividing one integer by another integer, the result is not always an integer. For instance, 7 divided by 2 is not a whole number but 3.5. One way to ensure that the result is an integer is to round
Round or rounds may refer to:
Mathematics and science
* Having no sharp corners, as an ellipse, circle, or sphere
* Rounding, reducing the number of significant figures in a number
* Round number, ending with one or more zeroes
* Round (crypt ...
the result to a whole number. However, this method leads to inaccuracies as the original value is altered. Another method is to perform the division only partially and retain the remainder
In mathematics, the remainder is the amount "left over" after performing some computation. In arithmetic, the remainder is the integer "left over" after dividing one integer by another to produce an integer quotient ( integer division). In a ...
. For example, 7 divided by 2 is 3 with a remainder of 1. These difficulties are avoided by rational number arithmetic, which allows for the exact representation of fractions.
A simple method to calculate exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
is by repeated multiplication. For instance, the exponentiation of can be calculated as . A more efficient technique used for large exponents is exponentiation by squaring
In mathematics and computer programming, exponentiating by squaring is a general method for fast computation of large positive integer powers of a number, or more generally of an element of a semigroup, like a polynomial or a square matrix. Some ...
. It breaks down the calculation into a number of squaring operations. For example, the exponentiation can be written as . By taking advantage of repeated squaring operations, only 7 individual operations are needed rather than the 64 operations required for regular repeated multiplication. Methods to calculate logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
s include the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
and continued fraction
A continued fraction is a mathematical expression that can be written as a fraction with a denominator that is a sum that contains another simple or continued fraction. Depending on whether this iteration terminates with a simple fraction or not, ...
s. Integer arithmetic is not closed under logarithm and under exponentiation with negative exponents, meaning that the result of these operations is not always an integer.
Number theory
Number theory studies the structure and properties of integers as well as the relations and laws between them. Some of the main branches of modern number theory includeelementary number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for exampl ...
, analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dir ...
, algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ob ...
, and geometric number theory
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
. Elementary number theory studies aspects of integers that can be investigated using elementary methods. Its topics include divisibility
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a ''Multiple (mathematics), multiple'' of m. An integer n is divis ...
, factorization
In mathematics, factorization (or factorisation, see American and British English spelling differences#-ise, -ize (-isation, -ization), English spelling differences) or factoring consists of writing a number or another mathematical object as a p ...
, and primality
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. Analytic number theory, by contrast, relies on techniques from analysis and calculus. It examines problems like how prime numbers are distributed and the claim that every even number is a sum of two prime numbers. Algebraic number theory employs algebraic structures to analyze the properties of and relations between numbers. Examples are the use of fields
Fields may refer to:
Music
*Fields (band), an indie rock band formed in 2006
* Fields (progressive rock band), a progressive rock band formed in 1971
* ''Fields'' (album), an LP by Swedish-based indie rock band Junip (2010)
* "Fields", a song by ...
and rings, as in algebraic number field
In mathematics, an algebraic number field (or simply number field) is an extension field K of the field of rational numbers such that the field extension K / \mathbb has finite degree (and hence is an algebraic field extension).
Thus K is a ...
s like the ring of integers
In mathematics, the ring of integers of an algebraic number field K is the ring of all algebraic integers contained in K. An algebraic integer is a root of a monic polynomial with integer coefficients: x^n+c_x^+\cdots+c_0. This ring is often de ...
. Geometric number theory uses concepts from geometry to study numbers. For instance, it investigates how lattice points with integer coordinates behave in a plane. Further branches of number theory are probabilistic number theory
In mathematics, Probabilistic number theory is a subfield of number theory, which explicitly uses probability to answer questions about the integers and integer-valued functions. One basic idea underlying it is that different prime numbers are, i ...
, which employs methods from probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
, combinatorial number theory, which relies on the field of combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...
, computational number theory
In mathematics and computer science, computational number theory, also known as algorithmic number theory, is the study of
computational methods for investigating and solving problems in number theory and arithmetic geometry, including algorithm ...
, which approaches number-theoretic problems with computational methods, and applied number theory, which examines the application of number theory to fields like physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
, and cryptography
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logy, -logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of Adversary (cryptography), ...
.
Influential theorems in number theory include the fundamental theorem of arithmetic
In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 is prime or can be represented uniquely as a product of prime numbers, ...
, Euclid's theorem
Euclid's theorem is a fundamental statement in number theory that asserts that there are Infinite set, infinitely many prime number, prime numbers. It was first proven by Euclid in his work ''Euclid's Elements, Elements''. There are several proof ...
, and Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive number, positive integers , , and satisfy the equation for any integer value of greater than . The cases ...
. According to the fundamental theorem of arithmetic, every integer greater than 1 is either a prime number or can be represented as a unique product of prime numbers. For example, the number 18 is not a prime number and can be represented as , all of which are prime numbers. The number 19, by contrast, is a prime number that has no other prime factorization. Euclid's theorem states that there are infinitely many prime numbers. Fermat's Last Theorem is the statement that no positive integer values exist for , , and that solve the equation if is greater than .
Rational number arithmetic
Rational number arithmetic is the branch of arithmetic that deals with the manipulation of numbers that can be expressed as aratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of two integers. Most arithmetic operations on rational numbers can be calculated by performing a series of integer arithmetic operations on the numerators and the denominators of the involved numbers. If two rational numbers have the same denominator then they can be added by adding their numerators and keeping the common denominator. For example, . A similar procedure is used for subtraction. If the two numbers do not have the same denominator then they must be transformed to find a common denominator. This can be achieved by scaling the first number with the denominator of the second number while scaling the second number with the denominator of the first number. For instance, .
Two rational numbers are multiplied by multiplying their numerators and their denominators respectively, as in . Dividing one rational number by another can be achieved by multiplying the first number with the reciprocal of the second number. This means that the numerator and the denominator of the second number change position. For example, . Unlike integer arithmetic, rational number arithmetic is closed under division as long as the divisor is not 0.
Both integer arithmetic and rational number arithmetic are not closed under exponentiation and logarithm. One way to calculate exponentiation with a fractional exponent is to perform two separate calculations: one exponentiation using the numerator of the exponent followed by drawing the nth root
In mathematics, an th root of a number is a number which, when raised to the power of , yields : r^n = \underbrace_ = x.
The positive integer is called the ''index'' or ''degree'', and the number of which the root is taken is the ''ra ...
of the result based on the denominator of the exponent. For example,