Apparent Size on:
[Wikipedia]
[Google]
[Amazon]
 The angular diameter, angular size, apparent diameter, or apparent size is an
The angular diameter, angular size, apparent diameter, or apparent size is an
 The angular diameter of a
The angular diameter of a
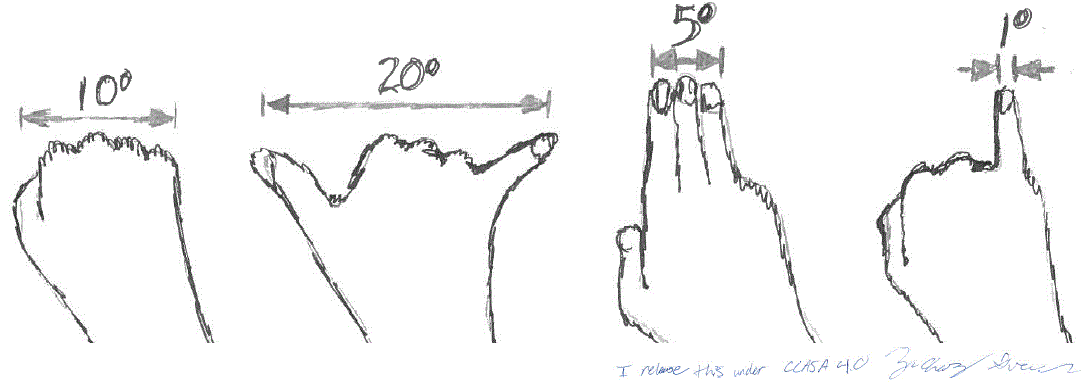 Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.
Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.
 The angular diameter of the Sun, as seen from Earth, is about 250,000 times that of
The angular diameter of the Sun, as seen from Earth, is about 250,000 times that of
Small-Angle Formula
(archived 7 October 1997)
{{Portal bar, Mathematics, Astronomy, Stars, Spaceflight, Outer space, Solar System, Science Elementary geometry Astrometry Angle Equations of astronomy
 The angular diameter, angular size, apparent diameter, or apparent size is an
The angular diameter, angular size, apparent diameter, or apparent size is an angular separation
Angular distance or angular separation is the measure of the angle between the orientation of two straight lines, rays, or vectors in three-dimensional space, or the central angle subtended by the radii through two points on a sphere. When t ...
(in units of angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight lines at a point. Formally, an angle is a figure lying in a plane formed by two rays, called the '' sides'' of the angle, sharing ...
) describing how large a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
or circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
appears from a given point of view. In the vision sciences, it is called the ''visual angle
Visual angle is the angle a viewed object subtends at the eye, usually stated in degrees of arc.
It also is called the object's angular size.
The diagram on the right shows an observer's eye looking at a frontal extent (the vertical arrow) th ...
'', and in optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
, it is the '' angular aperture'' (of a lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'') ...
). The angular diameter can alternatively be thought of as the angular displacement
The angular displacement (symbol θ, , or φ) – also called angle of rotation, rotational displacement, or rotary displacement – of a physical body is the angle (in units of radians, degrees, turns, etc.) through which the body rotates ( ...
through which an eye or camera must rotate to look from one side of an apparent circle to the opposite side.
A person can resolve with their naked eye
Naked eye, also called bare eye or unaided eye, is the practice of engaging in visual perception unaided by a magnification, magnifying, Optical telescope#Light-gathering power, light-collecting optical instrument, such as a telescope or microsc ...
s diameters down to about 1 arcminute
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a tu ...
(approximately 0.017° or 0.0003 radians). This corresponds to 0.3 m at a 1 km distance, or to perceiving Venus
Venus is the second planet from the Sun. It is often called Earth's "twin" or "sister" planet for having almost the same size and mass, and the closest orbit to Earth's. While both are rocky planets, Venus has an atmosphere much thicker ...
as a disk under optimal conditions.
Formulation
circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
whose plane is perpendicular to the displacement vector between the point of view and the center of said circle can be calculated using the formula
:
in which is the angular diameter (in units of angle, normally radians, sometimes in degrees, depending on the arctangent
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specific ...
implementation), is the linear diameter of the object (in units of length), and is the distance to the object (also in units of length). When , we have:
:,
and the result obtained is necessarily in radians
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
.
For a sphere
For a spherical object whose linear diameter equals and where is the distance to the of the sphere, the angular diameter can be found by the following modified formula : Such a different formulation is because the apparent edges of a sphere are its tangent points, which are closer to the observer than the center of the sphere, and have a distance between them which is smaller than the actual diameter. The above formula can be found by understanding that in the case of a spherical object, a right triangle can be constructed such that its three vertices are the observer, the center of the sphere, and one of the sphere's tangent points, with as the hypotenuse and as the sine. The formula is related to the zenith angle to the horizon, : where ''R'' is the radius of the sphere and ''h'' is the distance to the near of the sphere. The difference with the case of a perpendicular circle is significant only for spherical objects of large angular diameter, since the followingsmall-angle approximation
For small angles, the trigonometric functions sine, cosine, and tangent can be calculated with reasonable accuracy by the following simple approximations:
:
\begin
\sin \theta &\approx \tan \theta \approx \theta, \\ mu\cos \theta &\approx 1 - \t ...
s hold for small values of :
:
Estimating angular diameter using the hand
 Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.
Estimates of angular diameter may be obtained by holding the hand at right angles to a fully extended arm, as shown in the figure.
Use in astronomy
Inastronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
, the sizes of celestial object
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists within the observable universe. In astronomy, the terms ''object'' and ''body'' are of ...
s are often given in terms of their angular diameter as seen from Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
, rather than their actual sizes. Since these angular diameters are typically small, it is common to present them in arcsecond
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a tu ...
s (). An arcsecond is 1/3600th of one degree (1°) and a radian is 180/''π'' degrees. So one radian equals 3,600 × 180/ arcseconds, which is about 206,265 arcseconds (1 rad ≈ 206,264.806247"). Therefore, the angular diameter of an object with physical diameter ''d'' at a distance ''D'', expressed in arcseconds, is given by:
:.
These objects have an angular diameter of 1:
*an object of diameter 1 cm at a distance of 2.06 km
*an object of diameter 725.27 km at a distance of 1 astronomical unit
The astronomical unit (symbol: au or AU) is a unit of length defined to be exactly equal to . Historically, the astronomical unit was conceived as the average Earth-Sun distance (the average of Earth's aphelion and perihelion), before its m ...
(AU)
*an object of diameter 45 866 916 km at 1 light-year
A light-year, alternatively spelled light year (ly or lyr), is a unit of length used to express astronomical distances and is equal to exactly , which is approximately 9.46 trillion km or 5.88 trillion mi. As defined by the International Astr ...
*an object of diameter 1 AU (149 597 871 km) at a distance of 1 parsec
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to or (AU), i.e. . The parsec unit is obtained by the use of parallax and trigonometry, and ...
(pc)
Thus, the angular diameter of Earth's orbit
Earth orbits the Sun at an astronomical unit, average distance of , or 8.317 light-second, light-minutes, in a retrograde and prograde motion, counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes & ...
around the Sun
The Sun is the star at the centre of the Solar System. It is a massive, nearly perfect sphere of hot plasma, heated to incandescence by nuclear fusion reactions in its core, radiating the energy from its surface mainly as visible light a ...
as viewed from a distance of 1 pc is 2, as 1 AU is the mean radius of Earth's orbit.
The angular diameter of the Sun, from a distance of one light-year
A light-year, alternatively spelled light year (ly or lyr), is a unit of length used to express astronomical distances and is equal to exactly , which is approximately 9.46 trillion km or 5.88 trillion mi. As defined by the International Astr ...
, is 0.03, and that of Earth
Earth is the third planet from the Sun and the only astronomical object known to Planetary habitability, harbor life. This is enabled by Earth being an ocean world, the only one in the Solar System sustaining liquid surface water. Almost all ...
0.0003. The angular diameter 0.03 of the Sun given above is approximately the same as that of a human body at a distance of the diameter of Earth.
This table shows the angular sizes of noteworthy celestial bodies
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists within the observable universe. In astronomy, the terms ''object'' and ''body'' are of ...
as seen from Earth:
Sirius
Sirius is the brightest star in the night sky. Its name is derived from the Greek word (Latin script: ), meaning 'glowing' or 'scorching'. The star is designated Canis Majoris, Latinized to Alpha Canis Majoris, and abbr ...
. (Sirius has twice the diameter and its distance is 500,000 times as much; the Sun is 1010 times as bright, corresponding to an angular diameter ratio of 105, so Sirius is roughly 6 times as bright per unit solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poin ...
.)
The angular diameter of the Sun is also about 250,000 times that of Alpha Centauri A (it has about the same diameter and the distance is 250,000 times as much; the Sun is 4×1010 times as bright, corresponding to an angular diameter ratio of 200,000, so Alpha Centauri A is a little brighter per unit solid angle).
The angular diameter of the Sun is about the same as that of the Moon
The Moon is Earth's only natural satellite. It Orbit of the Moon, orbits around Earth at Lunar distance, an average distance of (; about 30 times Earth diameter, Earth's diameter). The Moon rotation, rotates, with a rotation period (lunar ...
. (The Sun's diameter is 400 times as large and its distance also; the Sun is 200,000 to 500,000 times as bright as the full Moon (figures vary), corresponding to an angular diameter ratio of 450 to 700, so a celestial body with a diameter of 2.5–4 and the same brightness per unit solid angle would have the same brightness as the full Moon.)
Even though Pluto is physically larger than Ceres, when viewed from Earth (e.g., through the Hubble Space Telescope
The Hubble Space Telescope (HST or Hubble) is a space telescope that was launched into low Earth orbit in 1990 and remains in operation. It was not the Orbiting Solar Observatory, first space telescope, but it is one of the largest and most ...
) Ceres has a much larger apparent size.
Angular sizes measured in degrees are useful for larger patches of sky. (For example, the three stars of the Belt cover about 4.5° of angular size.) However, much finer units are needed to measure the angular sizes of galaxies, nebulae, or other objects of the night sky
The night sky is the nighttime appearance of celestial objects like stars, planets, and the Moon, which are visible in a clear sky between sunset and sunrise, when the Sun is below the horizon.
Natural light sources in a night sky include moonlig ...
.
Degrees, therefore, are subdivided as follows:
* 360 degrees (°) in a full circle
* 60 arc-minutes () in one degree
* 60 arc-seconds () in one arc-minute
To put this in perspective, the full Moon as viewed from Earth is about °, or 30 (or 1800). The Moon's motion across the sky can be measured in angular size: approximately 15° every hour, or 15 per second. A one-mile-long line painted on the face of the Moon would appear from Earth to be about 1 in length.
In astronomy, it is typically difficult to directly measure the distance to an object, yet the object may have a known physical size (perhaps it is similar to a closer object with known distance) and a measurable angular diameter. In that case, the angular diameter formula can be inverted to yield the angular diameter distance
Angular may refer to:
Anatomy
* Angular artery, the terminal part of the facial artery
* Angular bone, a large bone in the lower jaw of amphibians and reptiles
* Angular incisure, a small anatomical notch on the stomach
* Angular gyrus, a regi ...
to distant objects as
:
In non-Euclidean space, such as our expanding universe, the angular diameter distance is only one of several definitions of distance, so that there can be different "distances" to the same object. See Distance measures (cosmology).
Non-circular objects
Manydeep-sky object
A deep-sky object (DSO) is any astronomical object that is not an individual star or Solar System object (such as Sun, Moon, planet, comet, etc.). The classification is used for the most part by amateur astronomers to denote visually observed fa ...
s such as galaxies
A galaxy is a system of stars, stellar remnants, interstellar gas, dust, and dark matter bound together by gravity. The word is derived from the Greek ' (), literally 'milky', a reference to the Milky Way galaxy that contains the Solar Sys ...
and nebula
A nebula (; or nebulas) is a distinct luminescent part of interstellar medium, which can consist of ionized, neutral, or molecular hydrogen and also cosmic dust. Nebulae are often star-forming regions, such as in the Pillars of Creation in ...
e appear non-circular and are thus typically given two measures of diameter: major axis and minor axis. For example, the Small Magellanic Cloud
The Small Magellanic Cloud (SMC) is a dwarf galaxy near the Milky Way. Classified as a dwarf irregular galaxy, the SMC has a D25 isophotal diameter of about , and contains several hundred million stars. It has a total mass of approximately 7 bill ...
has a visual apparent diameter of × .
Defect of illumination
Defect of illumination is the maximum angular width of the unilluminated part of a celestial body seen by a given observer. For example, if an object is 40 of arc across and is 75% illuminated, the defect of illumination is 10.See also
*Angular diameter distance
Angular may refer to:
Anatomy
* Angular artery, the terminal part of the facial artery
* Angular bone, a large bone in the lower jaw of amphibians and reptiles
* Angular incisure, a small anatomical notch on the stomach
* Angular gyrus, a regi ...
* Angular resolution
Angular resolution describes the ability of any image-forming device such as an Optical telescope, optical or radio telescope, a microscope, a camera, or an Human eye, eye, to distinguish small details of an object, thereby making it a major det ...
* Apparent magnitude
Apparent magnitude () is a measure of the Irradiance, brightness of a star, astronomical object or other celestial objects like artificial satellites. Its value depends on its intrinsic luminosity, its distance, and any extinction (astronomy), ...
* List of stars with resolved images
* Moon illusion
The Moon illusion is the optical illusion of the Moon appearing larger near the horizon than it does higher up in the sky. It has been known since ancient times and recorded by various cultures.
The explanation of this illusion is still debate ...
* Perceived visual angle
* Solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poin ...
* Visual acuity
Visual acuity (VA) commonly refers to the clarity of visual perception, vision, but technically rates an animal's ability to recognize small details with precision. Visual acuity depends on optical and neural factors. Optical factors of the eye ...
* Visual angle
Visual angle is the angle a viewed object subtends at the eye, usually stated in degrees of arc.
It also is called the object's angular size.
The diagram on the right shows an observer's eye looking at a frontal extent (the vertical arrow) th ...
References
External links
Small-Angle Formula
(archived 7 October 1997)
{{Portal bar, Mathematics, Astronomy, Stars, Spaceflight, Outer space, Solar System, Science Elementary geometry Astrometry Angle Equations of astronomy