|
Uniform Electron Gas
Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting free electrons in a solid where the complementary positive charges are not atomic nuclei but instead an idealized background of uniform positive charge density. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions (due to like charge) without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations. At zero temperature, the properties of jellium depend solely upon the constant electronic density. This property lends it to a treatment within density functional theory; the formalism itself pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanical
Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have bound states that are quantized to discrete values of energy, momentum, angular momentum, and other quantities, in contrast to classical systems where these quantities can be measured co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Monte Carlo
Diffusion Monte Carlo (DMC) or diffusion quantum Monte Carlo is a quantum Monte Carlo method that uses a Green's function to calculate low-lying energies of a quantum many-body Hamiltonian. Introduction and motivation of the algorithm Diffusion Monte Carlo has the potential to be numerically exact, meaning that it can find the exact ground state energy for any quantum system within a given error, but approximations must often be made and their impact must be assessed in particular cases. When actually attempting the calculation, one finds that for bosons, the algorithm scales as a polynomial with the system size, but for fermions, DMC scales exponentially with the system size. This makes exact large-scale DMC simulations for fermions impossible; however, DMC employing a clever approximation known as the fixed-node approximation can still yield very accurate results. To motivate the algorithm, let's look at the Schrödinger equation for a particle in some potential in one dimensi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Monte Carlo
Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution (or an accurate approximation) of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem. Quantum Monte Carlo methods allow for a direct treatment and description of complex many-body effects encoded in the wave function, going beyond mean-field theory. In particular, there exist numerically exact and polynomially-scaling algorithms to exactly study static properties of boson systems without geometrical frustration. For fermions, there exist very good approximations to their static properties and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that are b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Gap
In solid-state physics and solid-state chemistry, a band gap, also called a bandgap or energy gap, is an energy range in a solid where no electronic states exist. In graphs of the electronic band structure of solids, the band gap refers to the energy difference (often expressed in electronvolts) between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote an electron from the valence band to the conduction band. The resulting conduction-band electron (and the electron hole in the valence band) are free to move within the crystal lattice and serve as charge carriers to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transition
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic State of matter, states of matter: solid, liquid, and gas, and in rare cases, plasma (physics), plasma. A phase of a thermodynamic system and the states of matter have uniform physical property, physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition States of matter Phase transitions commonly refer to when a substance tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferromagnetic
Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are noticeably attracted to a magnet, which is a consequence of their substantial magnetic permeability. Magnetic permeability describes the induced magnetization of a material due to the presence of an external magnetic field. For example, this temporary magnetization inside a steel plate accounts for the plate's attraction to a magnet. Whether or not that steel plate then acquires permanent magnetization depends on both the strength of the applied field and on the coercivity of that particular piece of steel (which varies with the steel's chemical composition and any heat treatment it may have undergone). In physics, multiple types of material magnetism have been distinguished. Ferromagnetism (along with the similar effec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paramagnetic
Paramagnetism is a form of magnetism whereby some materials are weakly attracted by an externally applied magnetic field, and form internal, induced magnetic fields in the direction of the applied magnetic field. In contrast with this behavior, diamagnetic materials are repelled by magnetic fields and form induced magnetic fields in the direction opposite to that of the applied magnetic field. Paramagnetic materials include most chemical elements and some compounds; they have a relative magnetic permeability slightly greater than 1 (i.e., a small positive magnetic susceptibility) and hence are attracted to magnetic fields. The magnetic moment induced by the applied field is linear in the field strength and rather weak. It typically requires a sensitive analytical balance to detect the effect and modern measurements on paramagnetic materials are often conducted with a SQUID magnetometer. Paramagnetism is due to the presence of unpaired electrons in the material, so most atom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Monte Carlo
Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution (or an accurate approximation) of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem. Quantum Monte Carlo methods allow for a direct treatment and description of complex many-body effects encoded in the wave function, going beyond mean-field theory. In particular, there exist numerically exact and polynomially-scaling algorithms to exactly study static properties of boson systems without geometrical frustration. For fermions, there exist very good approximations to their static properties and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that are b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. Atomic and molecular systems Within the Hartree–Fock method of quantum chemistry, the antisymmetric wave function is approximated by a single Slater determinant. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation within the Born–Oppenheimer approximation. Therefore, the Hartree–Fock limit is always above this exact energy. The difference is called the ''correlation energy'', a term coined by Löwdin. The concept of the correlation energy was studied earlier by Wigner. A certain amount of electron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
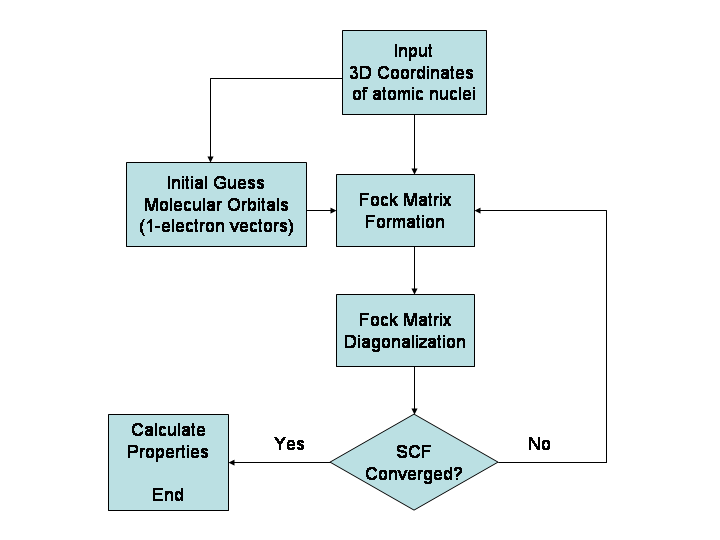
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |