|
Truncated Cubic Honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron. It is a self-dual tessellation with Schläfli symbol . John Horton Conway called this honeycomb a cubille. Description The cubic honeycomb is a space-filling or three-dimensional tessellation consisting of many cubes that attach each other to the faces; the cube is known as cell of a honeycomb. The parallelepiped is the member of a parallelohedron, generated from three line segments that are not all parallel to a common plane. The cube is the special case of a parallelepiped for having the most symmetric form, generated by three perpendicular unit-length line segments. In three-dimensional space, the cubic honeycomb is the only proper regular space-filling tessellation. It is self-dual. Related honeycombs The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Cubic Honeycomb
Partial may refer to: Mathematics *Partial derivative, derivative with respect to one of several variables of a function, with the other variables held constant ** ∂, a symbol that can denote a partial derivative, sometimes pronounced "partial dee" **Partial differential equation, a differential equation that contains unknown multivariable functions and their partial derivatives Other uses *Partial application, in computer science the process of fixing a number of arguments to a function, producing another function *Partial charge or net atomic charge, in chemistry a charge value that is not an integer or whole number *Partial fingerprint, impression of human fingers used in criminology or forensic science *Partial seizure or focal seizure, a seizure that initially affects only one hemisphere of the brain * Partial or Part score, in contract bridge a trick score less than 100, as well as other meanings * Partial or Partial wave, one sound wave of which a complex tone is composed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
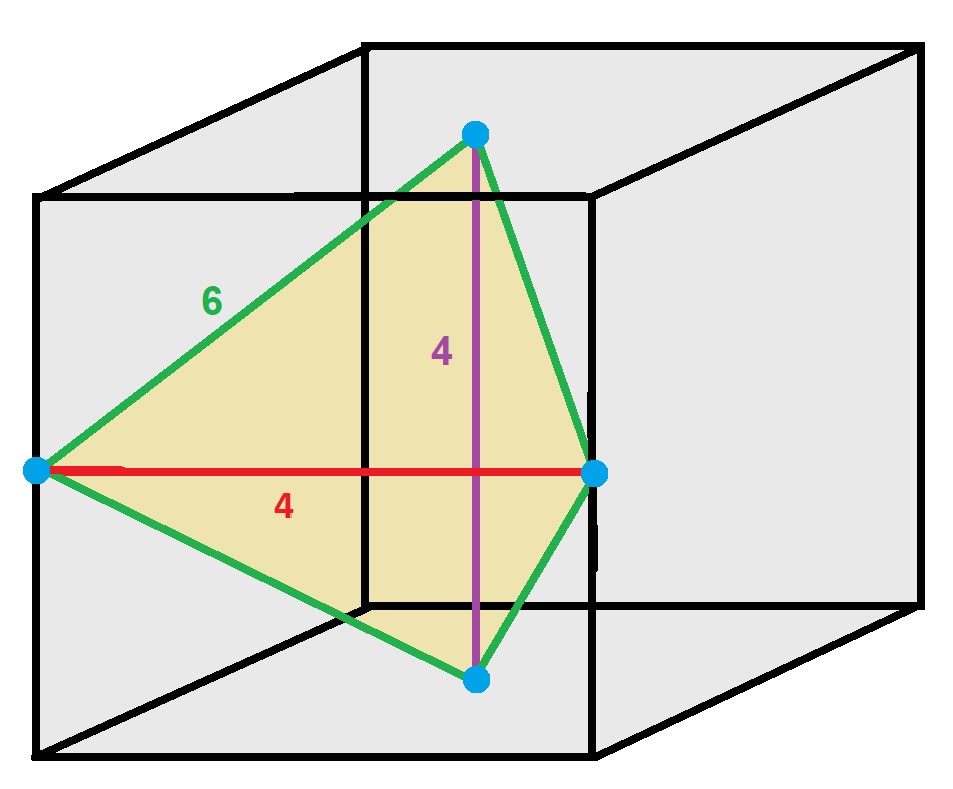
Oblate Octahedrille
The tetragonal disphenoid tetrahedral honeycomb is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of identical tetragonal disphenoidal cells. Cells are face-transitive with 4 identical isosceles triangle faces. John Horton Conway calls it an ''oblate tetrahedrille'' or shortened to ''obtetrahedrille''. Symmetry of Things, Table 21.1. Prime Architectonic and Catopric tilings of space, p. 293, 295. A cell can be seen as 1/12 of a translational cube, with its vertices centered on two faces and two edges. Four of its edges belong to 6 cells, and two edges belong to 4 cells. : The tetrahedral disphenoid honeycomb is the dual of the uniform bitruncated cubic honeycomb. Its vertices form the A / D lattice, which is also known as the Cubic_crystal_system, body-centered cubic lattice. Geometry This honeycomb's vertex figure is a tetrakis cube: 24 disphenoids meet at each vertex. The union of these 24 disphenoids forms a rhombic dodec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Architectonic And Catoptric Tessellation
In geometry, John Horton Conway defines architectonic and catoptric tessellations as the Uniform convex honeycomb, uniform tessellations (or Honeycomb (geometry), honeycombs) of Euclidean 3-space with prime space groups and their Dual polytope, duals, as three-dimensional analogue of the Platonic, Archimedean, and Catalan tiling of the plane. The singular vertex figure of an architectonic tessellation is the dual of the Cell (geometry), cell of the corresponding catoptric tessellation, and vice versa. The cubic honeycomb, cubille is the only Platonic (regular) tessellation of 3-space, and is self-dual. There are other uniform honeycombs constructed as gyrations or Convex uniform honeycomb#Prismatic stacks, prismatic stacks (and their duals) which are excluded from these categories. Enumeration The pairs of architectonic and catoptric tessellations are listed below with their symmetry group. These tessellations only represent four symmetry space groups, and also all within the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Uniform Honeycomb
In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honeycombs are known: * the familiar cubic honeycomb and 7 truncations thereof; * the alternated cubic honeycomb and 4 truncations thereof; * 10 prismatic forms based on the #Prismatic_stacks, uniform plane tilings (11 if including the cubic honeycomb); * 5 modifications of some of the above by elongation and/or gyration. They can be considered the three-dimensional analogue to the List of uniform planar tilings, uniform tilings of the plane. The Voronoi diagram of any Lattice (group), lattice forms a convex uniform honeycomb in which the cells are zonohedra. History * 1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication ''On the Regular and Semi-Regular Figures in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face in the same or reverse order, and with the same angles between corresponding faces. Technically, one says that for any two vertices there exists a symmetry of the polytope mapping the first isometrically onto the second. Other ways of saying this are that the group of automorphisms of the polytope '' acts transitively'' on its vertices, or that the vertices lie within a single '' symmetry orbit''. All vertices of a finite -dimensional isogonal figure exist on an -sphere. The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed from modern ideas such as symmetry groups and graph theory. The pseudorhombicuboctahedronwhich is ''not'' isogonaldemonstrates that simply asserting that "all vertices look ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge-transitive
In geometry, a polytope (for example, a polygon or a polyhedron) or a Tessellation, tiling is isotoxal () or edge-transitive if its Symmetry, symmetries act Transitive group action, transitively on its Edge (geometry), edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a Translation (geometry), translation, Rotation (mathematics), rotation, and/or Reflection (mathematics), reflection that will move one edge to the other while leaving the region occupied by the object unchanged. Isotoxal polygons An isotoxal polygon is an even-sided i.e. equilateral polygon, but not all equilateral polygons are isotoxal. The Duality (mathematics)#Dimension-reversing dualities, duals of isotoxal polygons are isogonal polygons. Isotoxal 4n-gons are Central symmetry, centrally symmetric, thus are also zonogons. In general, a (non-regular) isotoxal 2n-gon has \mathrm_n, (^*nn) dihedral symmetry. For example, a (non-square) rhombus is an isotoxa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cell-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent but must be ''transitive'', i.e. must lie within the same '' symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by translations, rotations, and/or reflections that maps onto . For this reason, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an even number of faces. The dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezohedra are all isohedral. They are the duals of the (isogonal) Archimedean solids, prisms, and antiprisms, respectively. The Platonic solids, which are either se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal Disphenoid
In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,. sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron. All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths. Special cases and generalizations If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with Td tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangles, it is called a tetragonal disphenoid. In this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncation (geometry)
In geometry, a bitruncation is an operation on regular polytopes. The original edges are lost completely and the original faces remain as smaller copies of themselves. Bitruncated regular polytopes can be represented by an extended Schläfli symbol notation or In regular polyhedra and tilings For regular polyhedra (i.e. regular 3-polytopes), a ''bitruncated'' form is the truncated dual. For example, a bitruncated cube is a truncated octahedron. In regular 4-polytopes and honeycombs For a regular 4-polytope, a ''bitruncated'' form is a dual-symmetric operator. A bitruncated 4-polytope is the same as the bitruncated dual, and will have double the symmetry if the original 4-polytope is self-dual. A regular polytope (or honeycomb) will have its cells bitruncated into truncated cells, and the vertices are replaced by truncated cells. Self-dual 4-polytope/honeycombs An interesting result of this operation is that self-dual 4-polytope (and honeycombs) remain cell- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Square (geometry), squares), 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a 6-zonohedron. It is also the Goldberg polyhedron GIV(1,1), containing square and hexagonal faces. Like the cube, it can tessellate (or "pack") 3-dimensional space, as a permutohedron. The truncated octahedron was called the "mecon" by Buckminster Fuller. Its dual polyhedron is the tetrakis hexahedron. If the original truncated octahedron has unit edge length, its dual tetrakis hexahedron has edge lengths and . Classifications As an Archimedean solid A truncated octahedron is constructed from a regular octahedron by cutting off all vertices. This resulting polyhedron has six squares and eight hexagons, leaving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bitruncated Cubic Honeycomb
The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of truncated octahedron, truncated octahedra (or, equivalently, Bitruncation (geometry), bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedron, truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 Convex uniform honeycomb, uniform honeycombs. John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an ''oblate tetrahedrille'', also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces. Geometry It can be realized as the Voronoi tessellation of the body-centred cubic lattice. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |