|
Tricolorability
In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non- isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial. Rules of tricolorability In these rules a strand in a knot diagram will be a piece of the string that goes from one undercrossing to the next. A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:Weisstein, Eric W. (2010). ''CRC Concise Encyclopedia of Mathematics'', Second Edition, p.3045. . quoted at Accessed: May 5, 2013. :1. At least two colors must be used, and :2. At each crossing, the three incident strands are either all the same color or all different colors. Some references state instead that all three colors must be used.Gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tricoloring
In the mathematics, mathematical field of knot theory, the tricolorability of a knot (mathematics), knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an Knot invariant, isotopy invariant, and hence can be used to distinguish between two different (non-Regular isotopy, isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial. Rules of tricolorability In these rules a strand in a knot diagram will be a piece of the string that goes from one undercrossing to the next. A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:Weisstein, Eric W. (2010). ''CRC Concise Encyclopedia of Mathematics'', Second Edition, p.3045. . quoted at Accessed: May 5, 2013. :1. At least two colors must be used, and :2. At each crossing, the three incident strands are either all the same color or all different colors. Som ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tricolorable Knots And Links
In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non- isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial. Rules of tricolorability In these rules a strand in a knot diagram will be a piece of the string that goes from one undercrossing to the next. A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:Weisstein, Eric W. (2010). ''CRC Concise Encyclopedia of Mathematics'', Second Edition, p.3045. . quoted at Accessed: May 5, 2013. :1. At least two colors must be used, and :2. At each crossing, the three incident strands are either all the same color or all different colors. Some references state instead that all three colors must be used.Gi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trefoil Knot
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot (mathematics), knot. The trefoil can be obtained by joining the two loose ends of a common overhand knot, resulting in a knotted loop (topology), loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory. The trefoil knot is named after the three-leaf clover (or trefoil) plant. Descriptions The trefoil knot can be defined as the curve obtained from the following parametric equations: :\begin x &= \sin t + 2 \sin 2t \\ y &= \cos t - 2 \cos 2t \\ z &= -\sin 3t \end The (2,3)-torus knot is also a trefoil knot. The following parametric equations give a (2,3)-torus knot lying on torus (r-2)^2+z^2 = 1: :\begin x &= (2+\cos 3t) \cos 2t \\ y &= (2+\cos 3t )\sin 2t \\ z &= \sin 3t \end Any continuous deformation of the curve above is also considered a trefoil knot. Specifically, any curve Homotopy#Isotopy, isotopic to a trefoil knot is also co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Diagram
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental problem in knot the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fox N-coloring
In the mathematical field of knot theory, Fox ''n''-coloring is a method of specifying a representation of a knot group or a group of a link (not to be confused with a link group) onto the dihedral group of order ''n'' where ''n'' is an odd integer by coloring arcs in a link diagram (the representation itself is also often called a Fox ''n''-coloring). Ralph Fox discovered this method (and the special case of tricolorability) "in an effort to make the subject accessible to everyone" when he was explaining knot theory to undergraduate students at Haverford College in 1956. Fox ''n''-coloring is an example of a conjugation quandle. Definition Let ''L'' be a link, and let \pi be the fundamental group of its complement. A representation \rho of \pi onto D_ the dihedral group of order ''2n'' is called a Fox ''n''-coloring (or simply an ''n''-coloring) of ''L''. A link ''L'' which admits such a representation is said to be ''n''-colorable, and \rho is called an ''n''-coloring of ''L' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unknot
In the knot theory, mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a Knot (mathematics), knot tied into it, unknotted. To a knot theorist, an unknot is any embedding, embedded Topological sphere, topological circle in the 3-sphere that is ambient isotopy, ambient isotopic (that is, deformable) to a geometrically round circle, the standard unknot. The unknot is the only knot that is the boundary of an embedded disk (mathematics), disk, which gives the characterization that only unknots have Seifert surface, Seifert genus 0. Similarly, the unknot is the identity element with respect to the knot sum operation. Unknotting problem Deciding if a particular knot is the unknot was a major driving force behind knot invariants, since it was thought this approach would possibly give an efficient algorithm to unknotting problem, recognize the unknot from some presentation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (knot Theory)
In mathematical knot theory, a link is a collection of knots that do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a ''trivial'' reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link. For example, a co-dimension 2 link in 3-dimensional space is a subspace of 3-dimensional Euclidean space (or often the 3-sphere) whose connected components are homeomorphic to circles. The simplest nontrivial example of a link with more than one component is called the Hopf link, which consists of two circles (or unknots) linked together once. The circles in the Borromean rings are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link and in fact constitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a Graph (discrete mathematics), graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the Vertex (graph theory), vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an ''edge coloring'' assigns a color to each Edge (graph theory), edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each Face (graph theory), face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Invariant
In the mathematical field of knot theory, a knot invariant is a quantity (in a broad sense) defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers (algebraic), but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory (for example, "a ''knot invariant'' is a rule that assigns to any knot a quantity such that if and are equivalent then ."). Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics. Knot invariants are thus used in knot classification,Purcell, Jessica (2020). ''Hyperbolic Knot Theory'', p.7. American Mathematical Society. "A ''knot invariant'' is a function from the set of knots to some other set whose value depends only on the equiva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
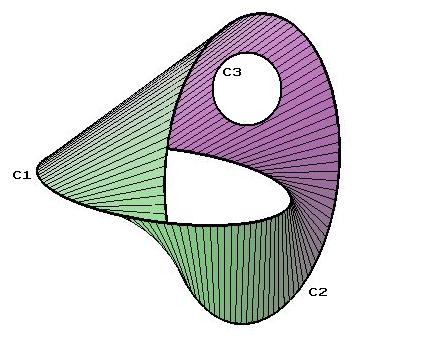
Torus Knot
In knot theory, a torus knot is a special kind of knot (mathematics), knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link (knot theory), link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers ''p'' and ''q''. A torus link arises if ''p'' and ''q'' are not coprime (in which case the number of components is greatest common divisor, gcd(''p, q'')). A torus knot is unknot, trivial (equivalent to the unknot) if and only if either ''p'' or ''q'' is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot. Geometrical representation A torus knot can be rendered geometrically in multiple ways which are topologically equivalent (see Properties below) but geometrically distinct. The convention used in this article and its figures is the following. The (''p'',''q'')-torus knot winds ''q'' times around a circle in the interior of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tricolor Invariance On Reidemeister III
A triband is a vexillological style which consists of three stripes arranged to form a flag. These stripes may be two or three colours, and may be charged with an emblem in the middle stripe. Not all tribands are tricolour flags, which requires three unique colours. Design Outside of the name, which requires three bands of colour, there are no other requirements for what a triband must look like, so there are many flags that look very different from each other but are all considered tribands. Some triband flags (e.g. those of Germany, Russia and the Netherlands) have their stripes positioned horizontally, while others (e.g. that of Italy) position the stripes vertically. Often the stripes on a triband are of equal length and width, though this is not always the case, as can be seen in the flags of Colombia and Canada. Symbols on tribands may be seals, such as on the Belizean flag, or any manner of emblems of significance to the area the flag represents, such as in the flags o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |