|
Trapezohedron
In geometry, an trapezohedron, -trapezohedron, -antidipyramid, -antibipyramid, or -deltohedron Remarks: the faces of a deltohedron are deltoids; a (non-twisted) kite or deltoid can be Dissection (geometry), dissected into two isosceles triangles or "deltas" (Δ), base-to-base. is the dual polyhedron of an antiprism. The faces of an are Congruence (geometry), congruent and symmetrically staggered; they are called #Symmetry, ''twisted kites''. With a higher symmetry, its faces are Kite (geometry), ''kites'' (sometimes also called ''trapezoids'', or ''deltoids''). The "" part of the name does not refer to faces here, but to two arrangements of each Vertex (geometry), vertices around an axis of symmetry. The dual antiprism has two actual faces. An trapezohedron can be Dissection (geometry), dissected into two equal Pyramid (geometry), pyramids and an antiprism. Terminology These figures, sometimes called deltohedra, are not to be confused with Deltahedron, deltahedra, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Trapezohedron
In geometry, a hexagonal trapezohedron or deltohedron is the fourth in an infinite series of trapezohedra which are dual polyhedra to the antiprisms. It has twelve faces which are congruence (geometry), congruent kite (geometry), kites. It can be described by the Conway polyhedron notation, Conway notation] It is an isohedral (face-transitive) figure, meaning that all its face (geometry), faces are the same. More specifically, all faces are not merely congruent but also ''transitive'', i.e. lie within the same ''symmetry orbit''. Convex polytope, Convex isohedral polyhedra are the shapes that will make fair dice. Symmetry The symmetry group, symmetry a hexagonal trapezohedron is D6d of order 24. The Point groups in three dimensions#Rotation groups, rotation group is D6 of order 12. Variations One degree of freedom within D6 symmetry changes the kites into congruent quadrilaterals with 3 edges lengths. In the limit, one edge of each quadrilateral goes to zero length, and these ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Trapezohedron
In geometry, a pentagonal trapezohedron is the third in the infinite family of trapezohedra, face-transitive polyhedra. Its dual polyhedron is the pentagonal antiprism. As a decahedron it has ten faces which are congruent kites. It can be decomposed into two pentagonal pyramids and a regular dodecahedron in the middle. 10-sided dice The pentagonal trapezohedron was patented for use as a gaming die (i.e. "game apparatus") in 1906. These dice are used for role-playing games that use percentile-based skills; however, a twenty-sided die can be labeled with the numbers 0-9 twice to use for percentages instead. Subsequent patents on ten-sided dice have made minor refinements to the basic design by rounding or truncating the edges. This enables the die to tumble so that the outcome is less predictable. One such refinement became notorious at the 1980 Gen Con when the patent was incorrectly thought to cover ten-sided dice in general. Ten-sided dice are commonly numbered from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its Face (geometry), faces are the same. More specifically, all faces must be not merely Congruence (geometry), congruent but must be ''transitive'', i.e. must lie within the same ''symmetry orbit''. In other words, for any two faces and , there must be a symmetry of the ''entire'' figure by Translation (geometry), translations, Rotation (mathematics), rotations, and/or Reflection (mathematics), reflections that maps onto . For this reason, Convex polytope, convex isohedral polyhedra are the shapes that will make fair dice. Isohedral polyhedra are called isohedra. They can be described by their face configuration. An isohedron has an Parity (mathematics), even number of faces. The Dual polyhedron, dual of an isohedral polyhedron is vertex-transitive, i.e. isogonal. The Catalan solids, the bipyramids, and the trapezo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiregular Polyhedron
In geometry, the term semiregular polyhedron (or semiregular polytope) is used variously by different authors. Definitions In its original definition, it is a polyhedron with regular polygonal faces, and a symmetry group which is transitive on its vertices; today, this is more commonly referred to as a uniform polyhedron (this follows from Thorold Gosset's 1900 definition of the more general semiregular polytope). These polyhedra include: *The thirteen Archimedean solids. ** The elongated square gyrobicupola (also called a pseudo-rhombicuboctahedron), a Johnson solid, has identical vertex figures (3.4.4.4) but because of a twist it is not vertex-transitive. Branko Grünbaum argued for including it as a 14th Archimedean solid. *An infinite series of convex prisms. *An infinite series of convex antiprisms (their semiregular nature was first observed by Kepler). These semiregular solids can be fully specified by a vertex configuration: a listing of the faces by number of sides, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombus, rhombi, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 types. As a Catalan solid, it is the dual polyhedron of the cuboctahedron. As a parallelohedron, the rhombic dodecahedron can be used to Honeycomb (geometry), tesselate its copies in space creating a rhombic dodecahedral honeycomb. There are some variations of the rhombic dodecahedron, one of which is the Bilinski dodecahedron. There are some stellations of the rhombic dodecahedron, one of which is the Escher's solid. The rhombic dodecahedron may also appear in nature (such as in the garnet crystal), the architectural philosophies, practical usages, and toys. As a Catalan solid Metric properties The rhombic dodecahedron is a polyhedron with twelve rhombus, rhombi, each of which long face-diagonal length is exactly \sqrt times the sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltoidal Icositetrahedron
In geometry, the deltoidal icositetrahedron (or trapezoidal icositetrahedron, tetragonal icosikaitetrahedron, tetragonal trisoctahedron, strombic icositetrahedron) is a Catalan solid. Its 24 faces are congruent kites. The deltoidal icositetrahedron, whose dual is the (uniform) rhombicuboctahedron, is tightly related to the pseudo-deltoidal icositetrahedron, whose dual is the pseudorhombicuboctahedron; but the actual and pseudo-d.i. are not to be confused with each other. Cartesian coordinates In the image above, the long body diagonals are those between opposite red vertices and between opposite blue vertices, and the short body diagonals are those between opposite yellow vertices.Cartesian coordinates for the vertices of the deltoidal icositetrahedron centered at the origin and with long body diagonal length 2 are: *red vertices (lying in 4-fold symmetry axes): :\left( \pm 1 , 0 , 0 \right) , \left( 0 , \pm 1 , 0 \right) , \left( 0 , 0 , \pm 1 \right) ; *blue ver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
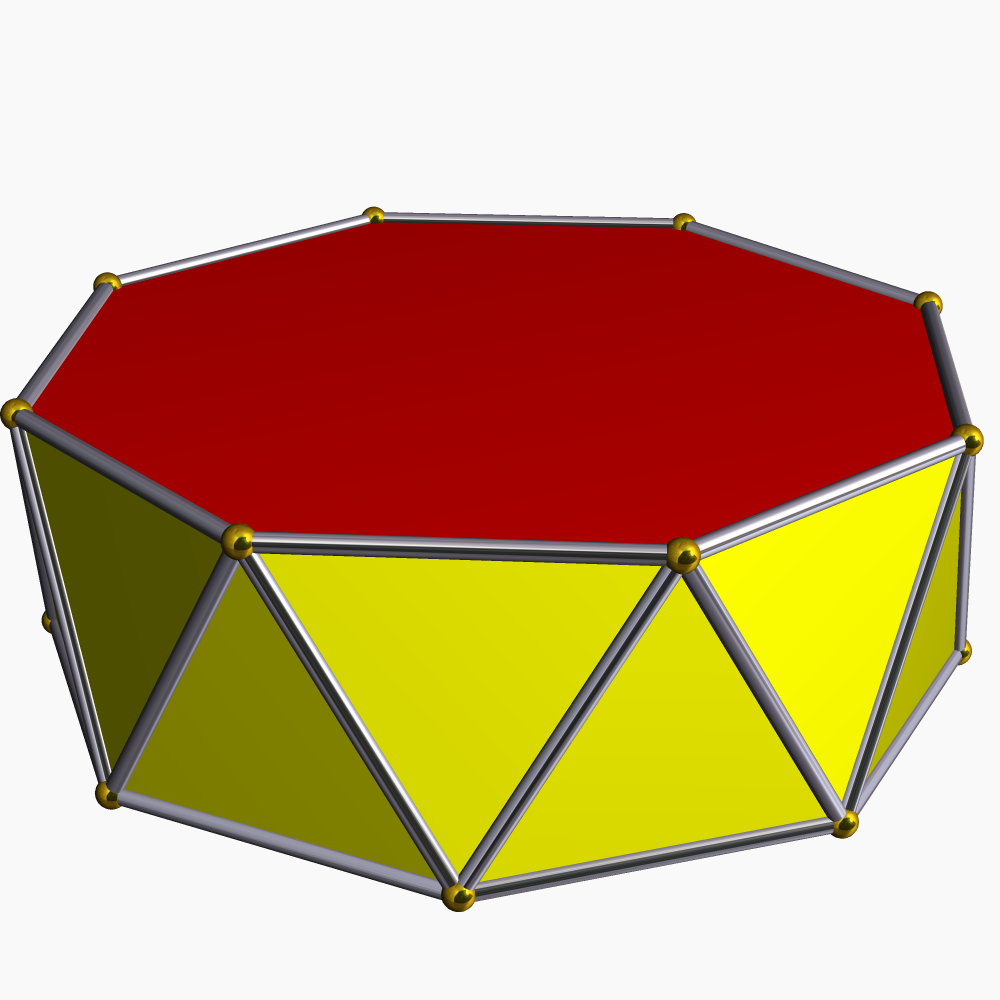
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal System
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices (an infinite array of discrete points). Space groups (symmetry groups of a configuration in space) are classified into crystal systems according to their point groups, and into lattice systems according to their Bravais lattices. Crystal systems that have space groups assigned to a common lattice system are combined into a crystal family. The seven crystal systems are ''triclinic'', ''monoclinic'', ''orthorhombic'', ''tetragonal'', ''trigonal'', ''hexagonal'', and ''cubic''. Informally, two crystals are in the same crystal system if they have similar symmetries (though there are many exceptions). Classifications Crystals can be classified in three ways: lattice systems, crystal systems and crystal families. The various classifications are often confused: in particular the trigonal crystal system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |