|
Tetrahedral
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Symmetry
image:tetrahedron.svg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation. The group of all (not necessarily orientation preserving) symmetries is isomorphic to the group S4, the symmetric group of permutations of four objects, since there is exactly one such symmetry for each permutation of the vertices of the tetrahedron. The set of orientation-preserving symmetries forms a group referred to as the alternating group, alternating subgroup A4 of S4. Details Chiral and full (or achiral tetrahedral symmetry and pyritohedral symmetry) are Point groups in three dimensions, discrete point symmetries (or equivalently, List of spherical symmetry groups, symmetries on the sphere). They are among the Crystal system#Overview of point groups by crystal system, crystallographic point gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Euler characteristic, duality, vertex figures, surface area, volume, interior lines, Dehn invariant, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (identical in shape and size) regular polygons (all angles congruent and all edge (geometry), edges congruent), and the same number of faces meet at each Vertex (geometry), vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato, who hypothesized in one of his dialogues, the ''Timaeus (dialogue), Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter delta resembling a triangular shape Δ. Deltahedra can be categorized by the property of convexity. The simplest convex deltahedron is the regular tetrahedron, a pyramid with four equilateral triangles. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compounds. There are infinitely many concave deltahedra. Strictly convex deltahedron A polyhedron is said to be ''convex'' if a line between any two of its vertices lies either within its interior or on its boundary, and additionally, if no two faces are coplanar (lying in the same plane) and no two edges are collinear (segments of the same line), it can be considered as being strictly convex. Of the eight convex deltahedra, three are Platonic solids and five are Johnson solids. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
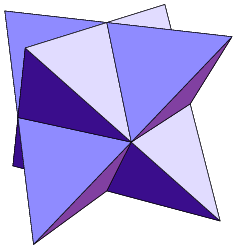
Stella Octangula
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's ''De Divina Proportione,'' 1509. It is the simplest of five regular polyhedral compounds, and the only regular polyhedral compound composed of only two polyhedra. It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. Construction and properties The stellated octahedron is constructed by a stellation of the regular octahedron. In other words, it ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex (geometry), apex. Each base edge (geometry), edge and apex form a triangle, called a lateral face. A pyramid is a cone, conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon (regular pyramids) or by cutting off the apex (truncated pyramid). It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are Self-dual polyhedron, self-dual. Etymology The word "pyramid" derives from the ancient Greek term "πυραμίς" (pyramis), which referred to a pyramid-shaped structure and a type of wheat cake. The term is rooted in the Greek "πυρ" (pyr, 'fire') and "άμις" (amis, 'vessel'), highlighting the shape's pointed, flame-like appearance. In Byzantine Greek, the term evolved to "πυραμίδα" (pyramída), continuing to denote pyramid structures. The Greek term " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stellated Octahedron
The stellated octahedron is the only stellation of the octahedron. It is also called the stella octangula (Latin for "eight-pointed star"), a name given to it by Johannes Kepler in 1609, though it was known to earlier geometers. It was depicted in Pacioli's ''Divina proportione, De Divina Proportione,'' 1509. It is the simplest of five regular polyhedral compounds, and the only regular polyhedral compound composed of only two polyhedra. It can be seen as a 3D extension of the hexagram: the hexagram is a two-dimensional shape formed from two overlapping equilateral triangles, central symmetry, centrally symmetric to each other, and in the same way the stellated octahedron can be formed from two centrally symmetric overlapping tetrahedra. This can be generalized to any desired amount of higher dimensions; the four-dimensional equivalent construction is the compound of two 5-cells. Construction and properties The stellated octahedron is constructed by a stellation of the regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Compound
In geometry, a polyhedral compound is a figure that is composed of several polyhedra sharing a common Centroid, centre. They are the three-dimensional analogs of star polygon#Regular compounds, polygonal compounds such as the hexagram. The outer Vertex (geometry), vertices of a compound can be connected to form a convex polyhedron called its convex hull. A compound is a faceting of its convex hull. Another convex polyhedron is formed by the small central space common to all members of the compound. This polyhedron can be used as the core for a set of stellations. Regular compounds A regular polyhedral compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. Unlike the case of polyhedra, this is not equivalent to the symmetry group acting transitively on its flag (geometry), flags; the compound of two tetrahedra is the only regular compound with that property. There are five regular compounds of polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygons
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex polygon, convex'' or ''star polygon, star''. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties These properties apply to all regular polygons, whether convex or star polygon, star: *A regular ''n''-sided polygon has rotational symmetry of order ''n''. *All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. *Together with the property of equal-length sides, this implies that every regular polygon also h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |