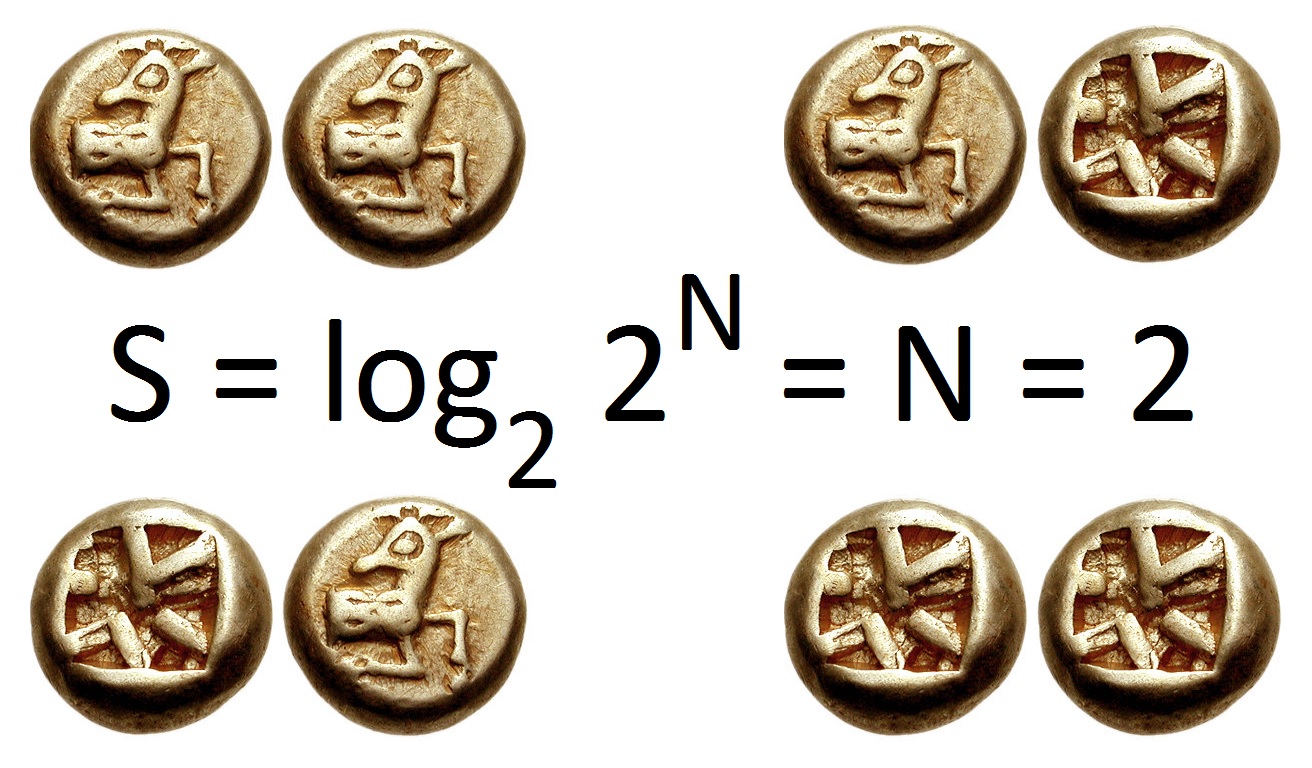|
Statistical Randomness
A numeric sequence is said to be statistically random when it contains no recognizable patterns or regularities; sequences such as the results of an ideal dice roll or the digits of π exhibit statistical randomness. Statistical randomness does not necessarily imply "true" randomness, i.e., objective unpredictability. Pseudorandomness is sufficient for many uses, such as statistics, hence the name ''statistical'' randomness. ''Global randomness'' and ''local randomness'' are different. Most philosophical conceptions of randomness are global—because they are based on the idea that "in the long run" a sequence looks truly random, even if certain sub-sequences would ''not'' look random. In a "truly" random sequence of numbers of sufficient length, for example, it is probable there would be long sequences of nothing but repeating numbers, though on the whole the sequence might be random. ''Local'' randomness refers to the idea that there can be minimum sequence lengths in whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diehard Tests
The diehard tests are a battery of statistical tests for measuring the quality of a random number generator. They were developed by George Marsaglia over several years and first published in 1995 on a CD-ROM of random numbers. Test overview ; Birthday spacings : Choose random points on a large interval. The spacings between the points should be asymptotically exponentially distributed. The name is based on the birthday paradox. ; Overlapping permutations : Analyze sequences of five consecutive random numbers. The 120 possible orderings should occur with statistically equal probability. ; Ranks of matrices : Select some number of bits from some number of random numbers to form a matrix over , then determine the rank of the matrix. Count the ranks. ; Monkey tests : Treat sequences of some number of bits as "words". Count the overlapping words in a stream. The number of "words" that do not appear should follow a known distribution. The name is based on the infinite monkey theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Density Estimation
In statistical signal processing, the goal of spectral density estimation (SDE) or simply spectral estimation is to estimate the spectral density (also known as the power spectral density) of a signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities. Some SDE techniques assume that a signal is composed of a limited (usually small) number of generating frequencies plus noise and seek to find the location and intensity of the generated frequencies. Others make no assumption on the number of components and seek to estimate the whole generating spectrum. Overview Spectrum analysis, also referred to as frequency domain analysis or spectral density estimation, is the technical process of decomposing a complex signal in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov–Smirnov Test
In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). In essence, the test answers the question "What is the probability that this collection of samples could have been drawn from that probability distribution?" or, in the second case, "What is the probability that these two sets of samples were drawn from the same (but unknown) probability distribution?". It is named after Andrey Kolmogorov and Nikolai Smirnov. The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|