|
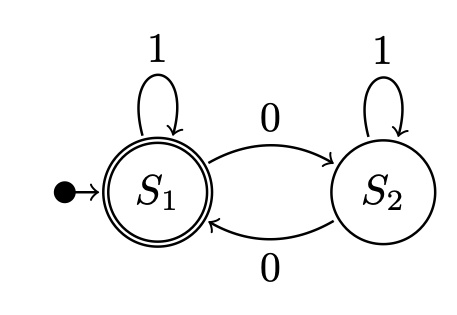
State Transition Table
In automata theory and sequential logic, a state-transition table is a table showing what state (or states in the case of a nondeterministic finite automaton) a finite-state machine will move to, based on the current state and other inputs. It is essentially a truth table in which the inputs include the current state along with other inputs, and the outputs include the next state along with other outputs. A state-transition table is one of many ways to specify a finite-state machine. Other ways include a state diagram. Common forms One-dimension State-transition tables are sometimes one-dimensional tables, also called ''characteristic tables''. They are much more like truth tables than their two-dimensional form. The single dimension indicates inputs, current states, next states and (optionally) outputs associated with the state transitions. : Two-dimensions State-transition tables are typically two-dimensional tables. There are two common ways for arranging them. In th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automata Theory
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to cognitive science and mathematical logic. The word ''automata'' comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
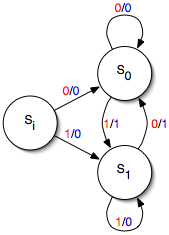
NFSM State Diagram
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if * each of its transitions is ''uniquely'' determined by its source state and input symbol, and * reading an input symbol is required for each state transition. A nondeterministic finite automaton (NFA), or nondeterministic finite-state machine, does not need to obey these restrictions. In particular, every DFA is also an NFA. Sometimes the term NFA is used in a narrower sense, referring to an NFA that is ''not'' a DFA, but not in this article. Using the subset construction algorithm, each NFA can be translated to an equivalent DFA; i.e., a DFA recognizing the same formal language. Like DFAs, NFAs only recognize regular languages. NFAs were introduced in 1959 by Michael O. Rabin and Dana Scott, who also showed their equivalence to DFAs. NFAs are used in the implementation of regular expressions: Thompson's construction is an algorithm for compiling a regular expression to an NFA tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mealy Machine
In the theory of computation, a Mealy machine is a finite-state machine whose output values are determined both by its current state and the current inputs. This is in contrast to a Moore machine, whose output values are determined solely by its current state. A Mealy machine is a deterministic finite-state transducer: for each state and input, at most one transition is possible. History The Mealy machine is named after George H. Mealy, who presented the concept in a 1955 paper, "A Method for Synthesizing Sequential Circuits". Formal definition A Mealy machine is a 6-tuple (S, S_0, \Sigma, \Lambda, T, G) consisting of the following: * a finite set of states S * a start state (also called initial state) S_0 which is an element of S * a finite set called the input alphabet \Sigma * a finite set called the output alphabet \Lambda * a transition function T : S \times \Sigma \rightarrow S mapping pairs of a state and an input symbol to the corresponding next state. * an output funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moore Machine
In the theory of computation, a Moore machine is a finite-state machine whose current output values are determined only by its current state. This is in contrast to a Mealy machine, whose output values are determined both by its current state and by the values of its inputs. Like other finite state machines, in Moore machines, the input typically influences the next state. Thus the input may indirectly influence subsequent outputs, but not the current or immediate output. The Moore machine is named after Edward F. Moore, who presented the concept in a 1956 paper, “ Gedanken-experiments on Sequential Machines.” Formal definition A Moore machine can be defined as a 6-tuple (S, s_0, \Sigma, O, \delta, G) consisting of the following: * A finite set of states S * A start state (also called initial state) s_0 which is an element of S * A finite set called the input alphabet \Sigma * A finite set called the output alphabet O * A transition function \delta : S \times \Sigma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Index Notation
In mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies according to the subject. In particular, there are different methods for referring to the elements of a list, a vector, or a matrix, depending on whether one is writing a formal mathematical paper for publication, or when one is writing a computer program. In mathematics It is frequently helpful in mathematics to refer to the elements of an array using subscripts. The subscripts can be integers or variables. The array takes the form of tensors in general, since these can be treated as multi-dimensional arrays. Special (and more familiar) cases are vectors (1d arrays) and matrices (2d arrays). The following is only an introduction to the concept: index notation is used in more detail in mathematics (particularly in the representation and manipulation of tensor operations). See the main article for further details. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Excitation Table
In electronics design, an excitation table shows the minimum inputs that are necessary to generate a particular next state (in other words, to "excite" it to the next state) when the current state is known. They are similar to truth tables and state tables, but rearrange the data so that the current state and next state are next to each other on the left-hand side of the table, and the inputs needed to make that state change happen are shown on the right side of the table. Flip-flop excitation tables In order to complete the excitation table of a flip-flop, one needs to draw the Q(t) and Q(t + 1) for all possible cases (e.g., 00, 01, 10, and 11), and then make the value of flip-flop such that on giving this value, one shall receive the input as Q(t + 1) as desired. T flip-flop The characteristic equation of a T flip-flop is Q(\text) = TQ' + T'Q = T \oplus Q. SR flip-flop ("X" is "don't care") The characteristic equation of a SR flip-flop is Q(\text) = S + QR'. JK flip-flo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dataflow
In computing, dataflow is a broad concept, which has various meanings depending on the application and context. In the context of software architecture, data flow relates to stream processing or reactive programming. Software architecture Dataflow computing is a software paradigm based on the idea of representing computations as a directed graph, where nodes are computations and data flow along the edges. Dataflow can also be called stream processing or reactive programming. There have been multiple data-flow/stream processing languages of various forms (see Stream processing). Data-flow hardware (see Dataflow architecture) is an alternative to the classic von Neumann architecture. The most obvious example of data-flow programming is the subset known as reactive programming with spreadsheets. As a user enters new values, they are instantly transmitted to the next logical "actor" or formula for calculation. Distributed data flows have also been proposed as a programming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph (discrete mathematics), graph. The elements of the matrix (mathematics), matrix indicate whether pairs of Vertex (graph theory), vertices are Neighbourhood (graph theory), adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is Glossary of graph theory terms#undirected, undirected (i.e. all of its Glossary of graph theory terms#edge, edges are bidirectional), the adjacency matrix is symmetric matrix, symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are Incidence (graph), incident or not, and its degree matrix, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency List
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs. Implementation details An adjacency list representation for a graph associates each vertex in the graph with the collection of its neighbouring vertices or edges. There are many variations of this basic idea, differing in the details of how they implement the association between vertices and collections, in how they implement the collections, in whether they include both vertices and edges or only vertices as first class objects, and in what kinds of objects are used to represent the vertices and edges. * An implementation suggested by Guido van Rossum uses a hash table to associate each vertex in a graph with an array of adjacent vertices. In this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite-state Machine
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of ''State (computer science), states'' at any given time. The FSM can change from one state to another in response to some Input (computer science), inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—Deterministic finite automaton, deterministic finite-state machines and Nondeterministic finite automaton, non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nondeterministic Programming
A nondeterministic programming language is a programming language, language which can specify, at certain points in the Computer program, program (called "choice points"), various alternatives for Control flow, program flow. Unlike an Conditional (computer programming), if-then statement, the method of choice between these alternatives is not directly specified by the programmer; the program must decide at runtime (program lifecycle phase), run time between the alternatives, via some general method applied to all choice points. A programmer specifies a limited number of alternatives, but the program must later choose between them. ("Choose" is, in fact, a typical name for the nondeterministic operator.) A hierarchy of choice points may be formed, with higher-level choices leading to branches that contain lower-level choices within them. One method of choice is embodied in backtracking systems (such as Amb (evaluator), Amb, or unification in Prolog), in which some alternatives may " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Logic
In automata theory, sequential logic is a type of logic circuit whose output depends on the present value of its input signals and on the sequence of past inputs, the input history. This is in contrast to '' combinational logic'', whose output is a function of only the present input. That is, sequential logic has ''state'' (''memory'') while combinational logic does not. Sequential logic is used to construct finite-state machines, a basic building block in all digital circuitry. Virtually all circuits in practical digital devices are a mixture of combinational and sequential logic. A familiar example of a device with sequential logic is a television set with "channel up" and "channel down" buttons. Pressing the "up" button gives the television an input telling it to switch to the next channel above the one it is currently receiving. If the television is on channel 5, pressing "up" switches it to receive channel 6. However, if the television is on channel 8, pressing "up" switch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |