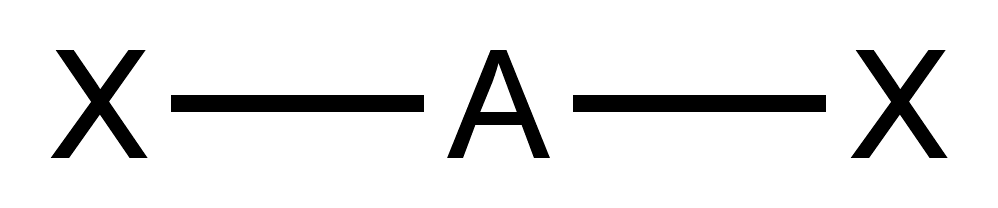|
Square Planar Molecular Geometry
In chemistry, the square planar molecular geometry describes the stereochemistry (spatial arrangement of atoms) that is adopted by certain chemical compounds. As the name suggests, molecules of this geometry have their atoms positioned at the corners. Examples Numerous compounds adopt this geometry, examples being especially numerous for transition metal complexes. The noble gas compound xenon tetrafluoride adopts this structure as predicted by VSEPR theory. The geometry is prevalent for transition metal complexes with d8 configuration, which includes Rh(I), Ir(I), Pd(II), Pt(II), and Au(III). Notable examples include the anticancer drugs cisplatin, tCl2(NH3)2 and carboplatin. Many homogeneous catalysts are square planar in their resting state, such as Wilkinson's catalyst and Crabtree's catalyst. Other examples include Vaska's complex and Zeise's salt. Certain ligands (such as porphyrins) stabilize this geometry. Splitting of d-orbitals A general d-orbital splitti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Symmetry In Three Dimensions
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2). Types There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation. ;Chiral: *''Dn'', [''n'',2]+, (22''n'') of order 2''n'' – dihedral symmetry or para-n-gonal group (abstract group: Dihedral group, ''Dihn''). ;Achiral: *''Dnh'', [''n'',2], (*22''n'') of order 4''n'' – prismatic symmetry or full ortho-n-gonal group (abstract group: ''Dihn'' × ''Z''2). *''Dnd'' (or ''Dnv''), [2''n'',2+], (2*''n'') of order 4''n'' – antiprismatic symmetry or full gyro-n-gonal group (abstract group: ''Dih''2''n''). For a given ''n'', all three have ''n''-fold rotational symmetry about one axis (rotation by an angle of 360°/''n'' does not change the object), and 2-fold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crabtree's Catalyst
Crabtree's catalyst is an organoiridium compound with the formula C5H5N">Tricyclohexylphosphine">P(C6H11)3pyridine">C5H5N/nowiki>PF6. It is a homogeneous catalyst for hydrogenation and hydrogen-transfer reactions, developed by Robert H. Crabtree. This air stable orange solid is commercially available and known for its directed hydrogenation to give trans stereoselectivity with respective of directing group. Structure and synthesis The cation has a square planar molecular geometry, as expected for a d8 complex. It is prepared from cyclooctadiene iridium chloride dimer. Reactivity Crabtree’s catalyst is effective for the hydrogenations of mono-, di-, tri-, and tetra-substituted substrates. Whereas Wilkinson’s catalyst and the Schrock–Osborn catalyst do not catalyze the hydrogenation of a tetrasubstituted olefin, Crabtree’s catalyst does so to at high turnover frequencies (table). : The catalyst is reactive at room temperature. The reaction is robust without drying sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
AXE Method
Valence shell electron pair repulsion (VSEPR) theory ( , ) is a conceptual model, model used in chemistry to predict the geometry of individual molecules from the number of electron pairs surrounding their central atoms. It is also named the Gillespie-Nyholm theory after its two main developers, Ronald Gillespie and Ronald Sydney Nyholm, Ronald Nyholm. The premise of VSEPR is that the valence electron pairs surrounding an atom tend to repel each other. The greater the repulsion, the higher in energy (less stable) the molecule is. Therefore, the VSEPR-predicted molecular geometry of a molecule is the one that has as little of this repulsion as possible. Gillespie has emphasized that the electron-electron repulsion due to the Pauli exclusion principle is more important in determining molecular geometry than the electrostatic repulsion. The insights of VSEPR theory are derived from topological analysis of the electron density of molecules. Such quantum chemical topology (QCT) metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Group
In geometry, a point group is a group (mathematics), mathematical group of symmetry operations (isometry, isometries in a Euclidean space) that have a Fixed point (mathematics), fixed point in common. The Origin (mathematics), coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension ''d'' is then a subgroup of the orthogonal group O(''d''). Point groups are used to describe the Symmetry (geometry), symmetries of geometric figures and physical objects such as molecular symmetry, molecules. Each point group can be Group representation, represented as sets of orthogonal matrix, orthogonal matrices ''M'' that transform point ''x'' into point ''y'' according to . Each element of a point group is either a Rotation (mathematics), rotation (determinant of ), or it is a Reflection (mathematics), reflection or improper rotation (determinant of ). The geometric symmetries of crystals are described by space groups, which allow T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irreducible Representation
In mathematics, specifically in the representation theory of groups and algebras, an irreducible representation (\rho, V) or irrep of an algebraic structure A is a nonzero representation that has no proper nontrivial subrepresentation (\rho, _W,W), with W \subset V closed under the action of \. Every finite-dimensional unitary representation on a Hilbert space V is the direct sum of irreducible representations. Irreducible representations are always indecomposable (i.e. cannot be decomposed further into a direct sum of representations), but the converse may not hold, e.g. the two-dimensional representation of the real numbers acting by upper triangular unipotent matrices is indecomposable but reducible. History Group representation theory was generalized by Richard Brauer from the 1940s to give modular representation theory, in which the matrix operators act on a vector space over a field K of arbitrary characteristic, rather than a vector space over the field of real number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedral Molecular Geometry
In chemistry, octahedral molecular geometry, also called square bipyramidal, describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The octahedron has eight faces, hence the prefix '' octa''. The octahedron is one of the Platonic solids, although octahedral molecules typically have an atom in their centre and no bonds between the ligand atoms. A perfect octahedron belongs to the point group Oh. Examples of octahedral compounds are sulfur hexafluoride SF6 and molybdenum hexacarbonyl Mo(CO)6. The term "octahedral" is used somewhat loosely by chemists, focusing on the geometry of the bonds to the central atom and not considering differences among the ligands themselves. For example, , which is not octahedral in the mathematical sense due to the orientation of the bonds, is referred to as octahedral. The concept of octahedral coordination geometry was developed by Alfred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D-orbital
In quantum mechanics, an atomic orbital () is a function describing the location and wave-like behavior of an electron in an atom. This function describes an electron's charge distribution around the atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus. Each orbital in an atom is characterized by a set of values of three quantum numbers , , and , which respectively correspond to electron's energy, its orbital angular momentum, and its orbital angular momentum projected along a chosen axis (magnetic quantum number). The orbitals with a well-defined magnetic quantum number are generally complex-valued. Real-valued orbitals can be formed as linear combinations of and orbitals, and are often labeled using associated harmonic polynomials (e.g., ''xy'', ) which describe their angular structure. An orbital can be occupied by a maximum of two electrons, each with its own projection of spin m_s. The simpl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D-orbital Splitting Diagrams Of Square Planar Complexes
In quantum mechanics, an atomic orbital () is a function describing the location and wave-like behavior of an electron in an atom. This function describes an electron's charge distribution around the atom's nucleus, and can be used to calculate the probability of finding an electron in a specific region around the nucleus. Each orbital in an atom is characterized by a set of values of three quantum numbers , , and , which respectively correspond to electron's energy, its orbital angular momentum, and its orbital angular momentum projected along a chosen axis (magnetic quantum number). The orbitals with a well-defined magnetic quantum number are generally complex-valued. Real-valued orbitals can be formed as linear combinations of and orbitals, and are often labeled using associated harmonic polynomials (e.g., ''xy'', ) which describe their angular structure. An orbital can be occupied by a maximum of two electrons, each with its own projection of spin m_s. The simple n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Porphyrin
Porphyrins ( ) are heterocyclic, macrocyclic, organic compounds, composed of four modified pyrrole subunits interconnected at their α carbon atoms via methine bridges (). In vertebrates, an essential member of the porphyrin group is heme, which is a component of hemoproteins, whose functions include carrying oxygen in the bloodstream. In plants, an essential porphyrin derivative is chlorophyll, which is involved in light harvesting and electron transfer in photosynthesis. The parent of porphyrins is porphine, a rare chemical compound of exclusively theoretical interest. Substituted porphines are called porphyrins. With a total of 26 π-electrons the porphyrin ring structure is a coordinated aromatic system. One result of the large conjugated system is that porphyrins absorb strongly in the visible region of the electromagnetic spectrum, i.e. they are deeply colored. The name "porphyrin" derives . Structure Porphyrin complexes consist of a square planar MN4 core. The p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeise's Salt
Zeise's salt, potassium trichloro(ethylene)platinate(II) hydrate, is the chemical compound with the formula K platinum.html" ;"title="/nowiki>platinum">PtCl3(C2H4)�H2O. The anion of this air-stable, yellow, coordination complex contains an hapticity">''η''2-ethylene ligand">ethylene.html" ;"title="hapticity">''η''2-ethylene">hapticity">''η''2-ethylene ligand. The anion features a platinum atom with a square planar geometry. The salt is of historical importance in the area of organometallic chemistry as one of the first examples of a transition metal alkene complex and is named for its discoverer, William Christopher Zeise. Preparation This compound is commercially available as a hydrate. The hydrate is commonly prepared from K2SnCl2. The water of hydration can be removed ''in vacuo''. Structure The alkene C=C bond is approximately perpendicular to the PtCl3 plane. In Zeise's salt and related compounds, the alkene rotates about the metal-alkene bond with a modest activatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |