|
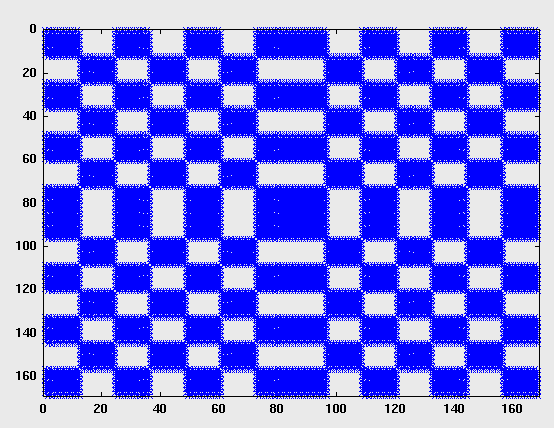
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Element Sparse Matrix
Finite may refer to: * Finite set, a set whose cardinality (number of elements) is some natural number * Finite verb, a verb form that has a subject, usually being inflected or marked for person and/or tense or aspect * "Finite", a song by Sara Groves from the album ''Invisible Empires'' See also * Finite number (other) * Finite part (other) * Finite map (other) * Finite presentation (other) * Finite type (other) * * Nonfinite (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band Matrix
In mathematics, particularly matrix theory, a band matrix or banded matrix is a sparse matrix whose non-zero entries are confined to a diagonal ''band'', comprising the main diagonal and zero or more diagonals on either side. Band matrix Bandwidth Formally, consider an ''n''×''n'' matrix ''A''=(''a''''i,j'' ). If all matrix elements are zero outside a diagonally bordered band whose range is determined by constants ''k''1 and ''k''2: :a_=0 \quad\mbox\quad ji+k_2; \quad k_1, k_2 \ge 0.\, then the quantities ''k''1 and ''k''2 are called the and , respectively. The of the matrix is the maximum of ''k''1 and ''k''2; in other words, it is the number ''k'' such that a_=0 if , i-j, > k . Examples *A band matrix with ''k''1 = ''k''2 = 0 is a diagonal matrix, with bandwidth 0. *A band matrix with ''k''1 = ''k''2 = 1 is a tridiagonal matrix, with bandwidth 1. *For ''k''1 = ''k''2 = 2 one has a pentadiagonal matrix and so on. * Triangular matrices **For ''k''1 = 0, ''k''2 = ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Gradient
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems. The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it. The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems. Description of the problem addre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative Method
In computational mathematics, an iterative method is a Algorithm, mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the ''i''-th approximation (called an "iterate") is derived from the previous ones. A specific implementation with Algorithm#Termination, termination criteria for a given iterative method like gradient descent, hill climbing, Newton's method, or Quasi-Newton method, quasi-Newton methods like Broyden–Fletcher–Goldfarb–Shanno algorithm, BFGS, is an algorithm of an iterative method or a method of successive approximation. An iterative method is called ''Convergent series, convergent'' if the corresponding sequence converges for given initial approximations. A mathematically rigorous convergence analysis of an iterative method is usually performed; however, heuristic-based iterative methods are also common. In contrast, direct methods attempt to solve the problem by a finit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cholesky Decomposition
In linear algebra, the Cholesky decomposition or Cholesky factorization (pronounced ) is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g., Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations. Statement The Cholesky decomposition of a Hermitian positive-definite matrix , is a decomposition of the form \mathbf = \mathbf^, where is a lower triangular matrix with real and positive diagonal entries, and * denotes the conjugate transpose of . Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition. The converse holds trivially: if can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symbolic Cholesky Decomposition
In the mathematical subfield of numerical analysis the symbolic Cholesky decomposition is an algorithm used to determine the non-zero pattern for the L factors of a symmetric sparse matrix when applying the Cholesky decomposition or variants. Algorithm Let A=(a_) \in \mathbb^ be a sparse symmetric positive definite matrix with elements from a field \mathbb, which we wish to factorize as A = LL^T\,. In order to implement an efficient sparse factorization it has been found to be necessary to determine the non zero structure of the factors before doing any numerical work. To write the algorithm down we use the following notation: * Let \mathcal_i and \mathcal_j be sets representing the non-zero patterns of columns and (below the diagonal only, and including diagonal elements) of matrices and respectively. * Take \min\mathcal_j to mean the smallest element of \mathcal_j. * Use a parent function \pi(i)\,\! to define the elimination tree within the matrix. The following algorith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block-diagonal Matrix
In mathematics, a block matrix or a partitioned matrix is a matrix (mathematics), matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or Partition of a set, partition it, into a collection of smaller matrices. For example, the 3x4 matrix presented below is divided by horizontal and vertical lines into four blocks: the top-left 2x3 block, the top-right 2x1 block, the bottom-left 1x3 block, and the bottom-right 1x1 block. : \left[ \begin a_ & a_ & a_ & b_ \\ a_ & a_ & a_ & b_ \\ \hline c_ & c_ & c_ & d \end \right] Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned. This notion can be made more precise for an n by m matrix M by partitioning n into a collection \text, and then partitioni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency List
In graph theory and computer science, an adjacency list is a collection of unordered lists used to represent a finite graph. Each unordered list within an adjacency list describes the set of neighbors of a particular vertex in the graph. This is one of several commonly used representations of graphs for use in computer programs. Implementation details An adjacency list representation for a graph associates each vertex in the graph with the collection of its neighbouring vertices or edges. There are many variations of this basic idea, differing in the details of how they implement the association between vertices and collections, in how they implement the collections, in whether they include both vertices and edges or only vertices as first class objects, and in what kinds of objects are used to represent the vertices and edges. * An implementation suggested by Guido van Rossum uses a hash table to associate each vertex in a graph with an array of adjacent vertices. In this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undirected Graph
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called '' vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing money is not necessarily reciprocated. Gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adjacency Matrix
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph (discrete mathematics), graph. The elements of the matrix (mathematics), matrix indicate whether pairs of Vertex (graph theory), vertices are Neighbourhood (graph theory), adjacent or not in the graph. In the special case of a finite simple graph, the adjacency matrix is a (0,1)-matrix with zeros on its diagonal. If the graph is Glossary of graph theory terms#undirected, undirected (i.e. all of its Glossary of graph theory terms#edge, edges are bidirectional), the adjacency matrix is symmetric matrix, symmetric. The relationship between a graph and the eigenvalues and eigenvectors of its adjacency matrix is studied in spectral graph theory. The adjacency matrix of a graph should be distinguished from its incidence matrix, a different matrix representation whose elements indicate whether vertex–edge pairs are Incidence (graph), incident or not, and its degree matrix, whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-dimensional Array
In computer science, an array is a data structure consisting of a collection of ''elements'' ( values or variables), of same memory size, each identified by at least one ''array index'' or ''key'', a collection of which may be a tuple, known as an index tuple. An array is stored such that the position (memory address) of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called a one-dimensional array. For example, an array of ten 32-bit (4-byte) integer variables, with indices 0 through 9, may be stored as ten words at memory addresses 2000, 2004, 2008, ..., 2036, (in hexadecimal: 0x7D0, 0x7D4, 0x7D8, ..., 0x7F4) so that the element with index ''i'' has the address 2000 + (''i'' × 4). The memory address of the first element of an array is called first address, foundation address, or base address. Because the mathematical concept of a matrix can be represented as a two-dimensional grid, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Main Diagonal
In linear algebra, the main diagonal (sometimes principal diagonal, primary diagonal, leading diagonal, major diagonal, or good diagonal) of a matrix A is the list of entries a_ where i = j. All off-diagonal elements are zero in a diagonal matrix. The following four matrices have their main diagonals indicated by red ones: \begin \color & 0 & 0\\ 0 & \color & 0\\ 0 & 0 & \color\end \qquad \begin \color & 0 & 0 & 0 \\ 0 & \color & 0 & 0 \\ 0 & 0 & \color & 0 \end \qquad \begin \color & 0 & 0 \\ 0 & \color & 0 \\ 0 & 0 & \color \\ 0 & 0 & 0 \end \qquad \begin \color & 0 & 0 & 0 \\ 0 & \color & 0 & 0 \\ 0 & 0 & \color & 0 \\ 0 & 0 & 0 & \color \end Square matrices For a square matrix, the ''diagonal'' (or ''main diagonal'' or ''principal diagonal'') is the diagonal line of entries running from the top-left corner to the bottom-right corner. For a matrix A with row index specified by i and column index specified by j, these would be entries A_ with i = j. For example, the iden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |