|
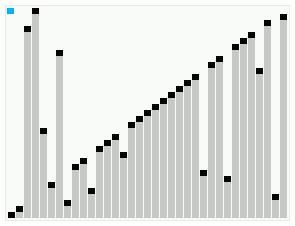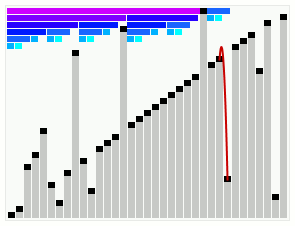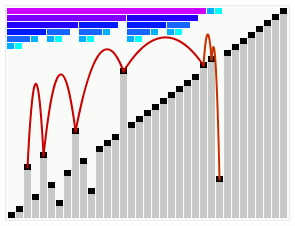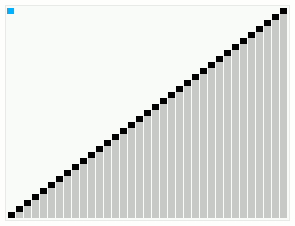
Smoothsort
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of , but it is not a stable sort. The advantage of smoothsort is that it comes closer to time if the input is already sorted to some degree, whereas heapsort averages regardless of the initial sorted state. Overview Like heapsort, smoothsort organizes the input into a priority queue and then repeatedly extracts the maximum. Also like heapsort, the priority queue is an implicit heap data structure (a heap-ordered implicit binary tree), which occupies a prefix of the array. Each extraction shrinks the prefix and adds the extracted element to a growing sorted suffix. When the prefix has shrunk to nothing, the array is completely sorted. Heapsort maps the binary tree to the array using a top-down breadth-first traversal of the tree; the array begins with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heapsort
In computer science, heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element from it and inserting it into the sorted region. Unlike selection sort, heapsort does not waste time with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly find the largest element in each step. Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantage of a more favorable worst-case runtime (and as such is used by Introsort as a fallback should it detect that quicksort is becoming degenerate). Heapsort is an in-place algorithm, but it is not a stable sort. Heapsort was invented by J. W. J. Williams in 1964. This was also the birth of the heap, presented ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonardo Number
The Leonardo numbers are a sequence of numbers given by the recurrence: : L(n) = \begin 1 & \mbox n = 0 \\ 1 & \mbox n = 1 \\ L(n - 1) + L(n - 2) + 1 & \mbox n > 1 \\ \end Edsger W. Dijkstra used them as an integral part of his smoothsort algorithm, and also analyzed them in some detail. A Leonardo prime is a Leonardo number that's also prime. Values The first few Leonardo numbers are :1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753, 1219, 1973, 3193, 5167, 8361, ... The first few Leonardo primes are : 3, 5, 41, 67, 109, 1973, 5167, 2692537, 11405773, 126491971, 331160281, 535828591, 279167724889, 145446920496281, 28944668049352441, 5760134388741632239, 63880869269980199809, 167242286979696845953, 597222253637954133837103, ... Modulo cycles The Leonardo numbers form a cycle in any modulo n≥2. An easy way to see it is: * If a pair of numbers modulo n appears twice in the sequence, then there's a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sorting Algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms (such as search and merge algorithms) that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output. Formally, the output of any sorting algorithm must satisfy two conditions: # The output is in monotonic order (each element is no smaller/larger than the previous element, according to the required order). # The output is a permutation (a reordering, yet retaining all of the original elements) of the input. For optimum efficiency, the input data should be stored in a data structure which allows random access rather than one that allows only sequential access. History and concepts From the beginning of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Sort
A sorting algorithm falls into the adaptive sort family if it takes advantage of existing order in its input. It benefits from the presortedness in the input sequence – or a limited amount of disorder for various definitions of measures of disorder – and sorts faster. Adaptive sorting is usually performed by modifying existing sorting algorithms. Motivation Comparison-based sorting algorithms have traditionally dealt with achieving an optimal bound of '' O''(''n'' log ''n'') when dealing with time complexity. Adaptive sort takes advantage of the existing order of the input to try to achieve better times, so that the time taken by the algorithm to sort is a smoothly growing function of the size of the sequence ''and'' the disorder in the sequence. In other words, the more presorted the input is, the faster it should be sorted. This is an attractive feature for a sorting algorithm because nearly sorted sequences are common in practice. Thus, the performance of existing sor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation (often a "less than or equal to" operator or a three-way comparison) that determines which of two elements should occur first in the final sorted list. The only requirement is that the operator forms a total preorder over the data, with: # if ''a'' ≤ ''b'' and ''b'' ≤ ''c'' then ''a'' ≤ ''c'' (transitivity) # for all ''a'' and ''b'', ''a'' ≤ ''b'' or ''b'' ≤ ''a'' (connexity). It is possible that both ''a'' ≤ ''b'' and ''b'' ≤ ''a''; in this case either may come first in the sorted list. In a stable sort, the input order determines the sorted order in this case. A metaphor for thinking about comparison sorts is that someone has a set of unlabelled weights and a balance scale. Their goal is to line up the weights in order by their weight without any information except that obtained by placing two weights on the scale and seeing which on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sorting Algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms (such as search and merge algorithms) that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output. Formally, the output of any sorting algorithm must satisfy two conditions: # The output is in monotonic order (each element is no smaller/larger than the previous element, according to the required order). # The output is a permutation (a reordering, yet retaining all of the original elements) of the input. For optimum efficiency, the input data should be stored in a data structure which allows random access rather than one that allows only sequential access. History and concepts From the beginning of c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adaptive Sort
A sorting algorithm falls into the adaptive sort family if it takes advantage of existing order in its input. It benefits from the presortedness in the input sequence – or a limited amount of disorder for various definitions of measures of disorder – and sorts faster. Adaptive sorting is usually performed by modifying existing sorting algorithms. Motivation Comparison-based sorting algorithms have traditionally dealt with achieving an optimal bound of '' O''(''n'' log ''n'') when dealing with time complexity. Adaptive sort takes advantage of the existing order of the input to try to achieve better times, so that the time taken by the algorithm to sort is a smoothly growing function of the size of the sequence ''and'' the disorder in the sequence. In other words, the more presorted the input is, the faster it should be sorted. This is an attractive feature for a sorting algorithm because nearly sorted sequences are common in practice. Thus, the performance of existing sor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Sort
In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms (such as search and merge algorithms) that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output. Formally, the output of any sorting algorithm must satisfy two conditions: # The output is in monotonic order (each element is no smaller/larger than the previous element, according to the required order). # The output is a permutation (a reordering, yet retaining all of the original elements) of the input. For optimum efficiency, the input data should be stored in a data structure which allows random access rather than one that allows only sequential access. History and concepts From the beginning of com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Priority Queue
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure in which each element additionally has a ''priority'' associated with it. In a priority queue, an element with high priority is served before an element with low priority. In some implementations, if two elements have the same priority, they are served according to the order in which they were enqueued; in other implementations ordering of elements with the same priority remains undefined. While coders often implement priority queues with heaps, they are conceptually distinct from heaps. A priority queue is a concept like a list or a map; just as a list can be implemented with a linked list or with an array, a priority queue can be implemented with a heap or with a variety of other methods such as an unordered array. Operations A priority queue must at least support the following operations: * ''is_empty'': check whether the queue has no elements. * ''insert_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Tree
In computer science, a binary tree is a k-ary k = 2 tree data structure in which each node has at most two children, which are referred to as the ' and the '. A recursive definition using just set theory notions is that a (non-empty) binary tree is a tuple (''L'', ''S'', ''R''), where ''L'' and ''R'' are binary trees or the empty set and ''S'' is a singleton set containing the root. Some authors allow the binary tree to be the empty set as well. From a graph theory perspective, binary (and K-ary) trees as defined here are arborescences. A binary tree may thus be also called a bifurcating arborescence—a term which appears in some very old programming books, before the modern computer science terminology prevailed. It is also possible to interpret a binary tree as an undirected, rather than a directed graph, in which case a binary tree is an ordered, rooted tree. Some authors use rooted binary tree instead of ''binary tree'' to emphasize the fact that the tree is roo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Heap
A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort. A binary heap is defined as a binary tree with two additional constraints: *Shape property: a binary heap is a '' complete binary tree''; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right. *Heap property: the key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node's children, according to some total order. Heaps where the parent key is greater than or equal to (≥) the child keys are called ''max-heaps''; those where it is less than or equal to (≤) are called ''min-heaps''. Efficient ( logarithmic time) algorithms are known for the two ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |