|
Radiation Zone
A radiative zone is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiative zone in the form of electromagnetic radiation as photons. Matter in a radiative zone is so dense that photons can travel only a short distance before they are absorbed or scattered by another particle, gradually shifting to longer wavelength as they do so. For this reason, it takes an average of 171,000 years for gamma rays from the core of the Sun to leave the radiative zone. Over this range, the temperature of the plasma drops from 15 million K near the core down to 1.5 million K at the base of the convection zone. Temperature gradient In a radiative zone, the temperature gradient—the change in temperature (''T'') as a function of radius (''r'')—is given by: : \frac\ =\ -\frac where ''κ''(''r'') is the opacity, ''ρ''(''r'') is the matter density, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radiation
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or a material medium. This includes: * ''electromagnetic radiation'' consisting of photons, such as radio waves, microwaves, infrared, visible light, ultraviolet, x-rays, and Gamma ray, gamma radiation (γ) * ''particle radiation'' consisting of particles of non-zero rest energy, such as alpha radiation (α), beta radiation (β), proton radiation and neutron radiation * ''acoustics, acoustic radiation'', such as ultrasound, sound, and seismic waves, all dependent on a physical transmission medium * ''gravitational radiation'', in the form of gravitational waves, ripples in spacetime Radiation is often categorized as either ''ionizing radiation, ionizing'' or ''non-ionizing radiation, non-ionizing'' depending on the energy of the radiated particles. Ionizing radiation carries more than 10 electron volt, electron volts (eV), which is enough to ionize atoms and molecul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monatomic Gas
In physics and chemistry, "monatomic" is a combination of the words "mono" and "atomic", and means "single atom". It is usually applied to gases: a monatomic gas is a gas in which atoms are not bound to each other. Examples at standard conditions of temperature and pressure include all the noble gases (helium, neon, argon, krypton, xenon, and radon), though all chemical elements will be monatomic in the gas phase at sufficiently high temperature (or very low pressure). The thermodynamic behavior of a monatomic gas is much simpler when compared to polyatomic gases because it is free of any rotational or vibrational energy. Noble gases The only chemical elements that are stable single atoms (so they are not molecules) at standard temperature and pressure (STP) are the noble gases. These are helium, neon, argon, krypton, xenon, and radon. Noble gases have a full outer valence shell making them rather non-reactive species. While these elements have been described historically as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Ledoux
Paul Ledoux (8 August 1914 – 6 October 1988) was a Belgian astrophysicist best known for his work on stellar stability and variability. With Theodore Walraven, he co-authored a seminal work on stellar oscillations. In 1964 Ledoux was awarded the Francqui Prize for Exact Sciences, and was awarded the Eddington Medal of the Royal Astronomical Society in 1972 for investigations into problems of stellar stability and variable stars A variable star is a star whose brightness as seen from Earth (its apparent magnitude) changes systematically with time. This variation may be caused by a change in emitted light or by something partly blocking the light, so variable stars are .... He was awarded the Janssen Medal of the French Academy of Sciences in 1976. Ledoux criterion In stellar astrophysics, Ledoux's name is now associated with the criterion under which material in a star becomes unstable to convection in the presence of a gradient of chemical composition. In hom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Criterion
In astrophysics, the Schwarzschild criterion indicates when a stellar medium is stable against convection when the rate of change in temperature'','' T, by altitude'','' z, satisfies : -\frac < \frac where is and is the at constant pressure. The criterion is named after its discoverer, .Martin Schwarzschild, Structure and Evolution of Stars, If a gas is u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the '' isentropic expansion factor'' and is denoted by (gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of sound i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the Displacement (fluid), displaced fluid. For this reason, an object with average density greater than the surrounding fluid tends to sink because its weight is greater than the weight of the fluid it displaces. If the objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as Work (thermodynamics), work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of fire, flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection Cell
In fluid dynamics, a convection cell is the phenomenon that occurs when density differences exist within a body of liquid or gas. These density differences result in rising and/or falling convection currents, which are the key characteristics of a convection cell. When a volume of fluid is heated, it expands and becomes less dense and thus more buoyant than the surrounding fluid. The colder, denser part of the fluid descends to settle below the warmer, less-dense fluid, and this causes the warmer fluid to rise. Such movement is called convection, and the moving body of liquid is referred to as a ''convection cell''. This particular type of convection, where a horizontal layer of fluid is heated from below, is known as Rayleigh–Bénard convection. Convection usually requires a gravitational field, but in microgravity experiments, thermal convection has been observed without gravitational effects. Fluids are generalized as materials that exhibit the property of Fluid dynamics, f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stellar Model
This glossary of astronomy is a list of definitions of terms and concepts relevant to astronomy and cosmology, their sub-disciplines, and related fields. Astronomy is concerned with the study of astronomical object, celestial objects and phenomena that originate outside the atmosphere of Earth. The field of astronomy features an extensive vocabulary and a significant amount of jargon. A B C D E F G H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrostatic Equilibrium
In fluid mechanics, hydrostatic equilibrium, also called hydrostatic balance and hydrostasy, is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planetary physics of Earth, the pressure-gradient force prevents gravity from collapsing the atmosphere of Earth into a thin, dense shell, whereas gravity prevents the pressure-gradient force from diffusing the atmosphere into outer space. In general, it is what causes objects in space to be spherical. Hydrostatic equilibrium is the distinguishing criterion between dwarf planets and small solar system bodies, and features in astrophysics and planetary geology. Said qualification of equilibrium indicates that the shape of the object is symmetrically rounded, mostly due to rotation, into an ellipsoid, where any irregular surface features are consequent to a relatively thin solid crust. In addition to the Sun, there are a dozen or s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
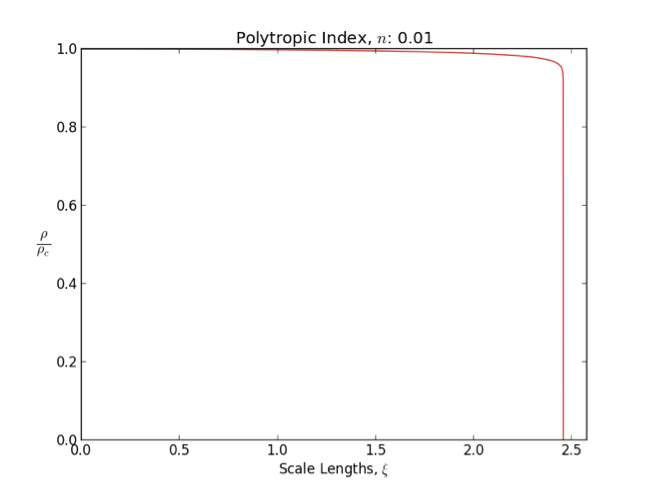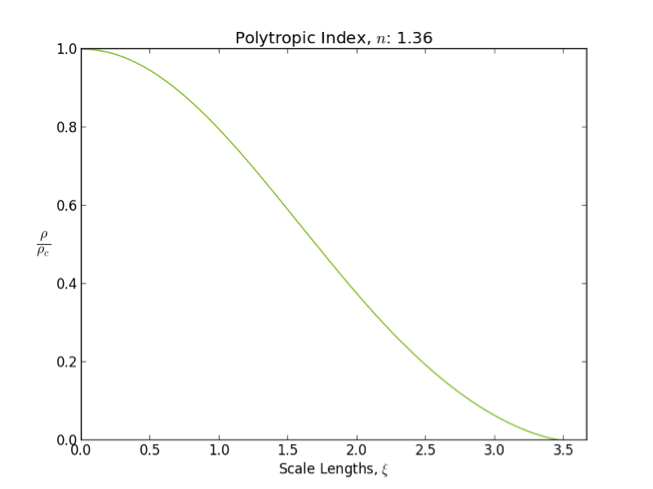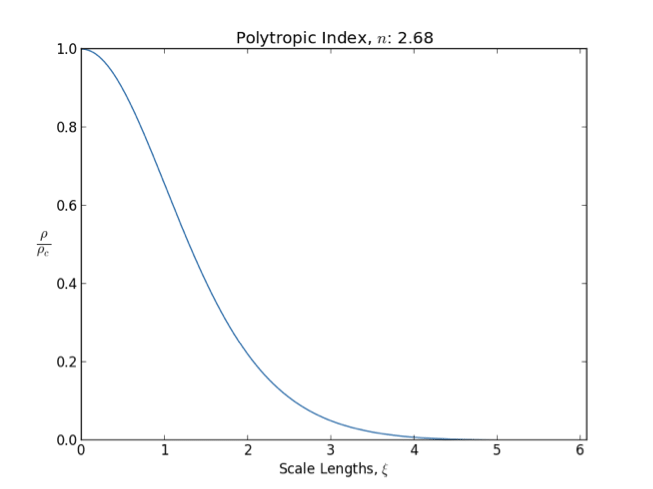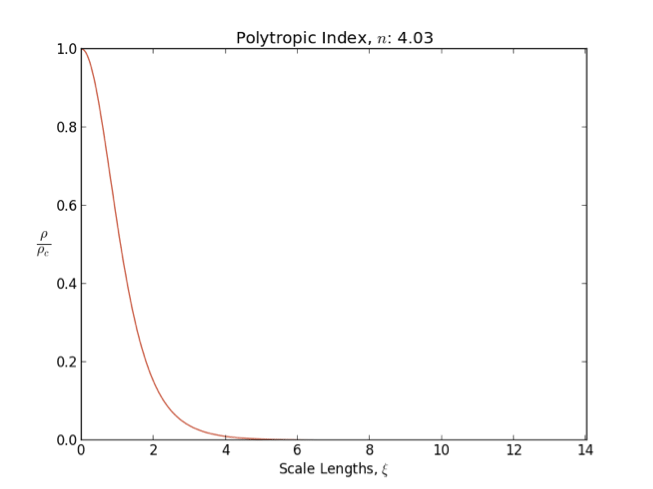
Polytrope
In astrophysics, a polytrope refers to a solution of the Lane–Emden equation in which the pressure depends upon the density in the form P = K \rho^ = K \rho^, where is pressure, is density and is a Constant (mathematics), constant of Proportionality (mathematics), proportionality. The constant is known as the polytropic index; note however that the polytropic index has an alternative definition as with ''n'' as the exponent. This relation need not be interpreted as an equation of state, which states ''P'' as a function of both ρ and ''T'' (the temperature); however in the particular case described by the polytrope equation there are other additional relations between these three quantities, which together determine the equation. Thus, this is simply a relation that expresses an assumption about the change of pressure with radius in terms of the change of density with radius, yielding a solution to the Lane–Emden equation. Sometimes the word ''polytrope'' may refer t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |