|
Quantum Monte Carlo
Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution (or an accurate approximation) of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem. Quantum Monte Carlo methods allow for a direct treatment and description of complex many-body effects encoded in the wave function, going beyond mean-field theory. In particular, there exist numerically exact and polynomially-scaling algorithms to exactly study static properties of boson systems without geometrical frustration. For fermions, there exist very good approximations to their static properties and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum System
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biological System
A biological system is a complex network which connects several biologically relevant entities. Biological organization spans several scales and are determined based different structures depending on what the system is. Examples of biological systems at the macro scale are populations of organisms. On the organ and tissue scale in mammals and other animals, examples include the circulatory system, the respiratory system, and the nervous system. On the micro to the nanoscopic scale, examples of biological systems are cells, organelles, macromolecular complexes and regulatory pathways. A biological system is not to be confused with a living system, such as a living organism. Organ and tissue systems These specific systems are widely studied in human anatomy and are also present in many other animals. * Respiratory system: the organs used for breathing, the pharynx, larynx, bronchi, lungs and diaphragm. * Digestive system: digestion and processing food with salivary g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Monte Carlo
Diffusion Monte Carlo (DMC) or diffusion quantum Monte Carlo is a quantum Monte Carlo method that uses a Green's function to solve the Schrödinger equation. DMC is potentially numerically exact, meaning that it can find the exact ground state energy within a given error for any quantum system. When actually attempting the calculation, one finds that for bosons, the algorithm scales as a polynomial with the system size, but for fermions, DMC scales exponentially with the system size. This makes exact large-scale DMC simulations for fermions impossible; however, DMC employing a clever approximation known as the fixed-node approximation can still yield very accurate results. The projector method To motivate the algorithm, let's look at the Schrödinger equation for a particle in some potential in one dimension: :i\frac=-\frac\frac + V(x)\Psi(x,t). We can condense the notation a bit by writing it in terms of an '' operator'' equation, with :H=-\frac\frac + V(x). So then we have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Monte Carlo
In computational physics, variational Monte Carlo (VMC) is a quantum Monte Carlo method that applies the variational method to approximate the ground state of a quantum system. The basic building block is a generic wave function , \Psi(a) \rangle depending on some parameters a . The optimal values of the parameters a is then found upon minimizing the total energy of the system. In particular, given the Hamiltonian \mathcal , and denoting with X a many-body configuration, the expectation value of the energy can be written as: E(a) = \frac = \frac . Following the Monte Carlo method for evaluating integrals, we can interpret \frac as a probability distribution function, sample it, and evaluate the energy expectation value E(a) as the average of the so-called local energy E_(X) = \frac . Once E(a) is known for a given set of variational parameters a , then optimization is performed in order to minimize the energy and obtain the best possible representation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-dependent Variational Monte Carlo
The time-dependent variational Monte Carlo (t-VMC) method is a quantum Monte Carlo approach to study the dynamics of closed, non-relativistic quantum systems in the context of the quantum many-body problem. It is an extension of the variational Monte Carlo method, in which a time-dependent pure quantum state is encoded by some variational wave function, generally parametrized as : \Psi(X,t) = \exp \left ( \sum_k a_k(t) O_k(X) \right ) where the complex-valued a_k(t) are time-dependent variational parameters, X denotes a many-body configuration and O_k(X) are time-independent operators that define the specific ansatz. The time evolution of the parameters a_k(t) can be found upon imposing a variational principle to the wave function. In particular one can show that the optimal parameters for the evolution satisfy at each time the equation of motion : i \sum_\langle O_k O_\rangle_t^c \dot_=\langle O_k \mathcal\rangle_t^c, where \mathcal is the Hamiltonian of the sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent ''mixed states''. Mixed states arise in quantum mechanics in two different situations: first when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and second when one wants to describe a physical system which is entangled with another, without describing their combined state. Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information. Definition an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Auxiliary-field Monte Carlo
Auxiliary-field Monte Carlo is a method that allows the calculation, by use of Monte Carlo techniques, of averages of operators in many-body quantum mechanical (Blankenbecler 1981, Ceperley 1977) or classical problems (Baeurle 2004, Baeurle 2003, Baeurle 2002a). Reweighting procedure and numerical sign problem The distinctive ingredient of "auxiliary-field Monte Carlo" is the fact that the interactions are decoupled by means of the application of the Hubbard–Stratonovich transformation, which permits the reformulation of many-body theory in terms of a scalar auxiliary-field representation. This reduces the many-body problem to the calculation of a sum or integral over all possible auxiliary-field configurations. In this sense, there is a trade-off: instead of dealing with one very complicated many-body problem, one faces the calculation of an infinite number of simple external-field problems. It is here, as in other related methods, that Monte Carlo enters the game in the guis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Integral Monte Carlo
Path integral Monte Carlo (PIMC) is a quantum Monte Carlo method used to solve quantum statistical mechanics problems numerically within the path integral formulation. The application of Monte Carlo methods to path integral simulations of condensed matter systems was first pursued in a key paper by John A. Barker. The method is typically (but not necessarily) applied under the assumption that symmetry or antisymmetry under exchange can be neglected, i.e., identical particles are assumed to be quantum Boltzmann particles, as opposed to fermion and boson particles. The method is often applied to calculate thermodynamic properties such as the internal energy, heat capacity, or Thermodynamic free energy, free energy. As with all Monte Carlo method based approaches, a large number of points must be calculated. In principle, as more path descriptors are used (these can be "replicas", "beads," or "Fourier coefficients," depending on what strategy is used to represent the paths), the mor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ground State
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state. In quantum field theory, the ground state is usually called the vacuum state or the vacuum. If more than one ground state exists, they are said to be degenerate. Many systems have degenerate ground states. Degeneracy occurs whenever there exists a unitary operator that acts non-trivially on a ground state and commutes with the Hamiltonian of the system. According to the third law of thermodynamics, a system at absolute zero temperature exists in its ground state; thus, its entropy is determined by the degeneracy of the ground state. Many systems, such as a perfect crystal lattice, have a unique ground state and therefore have zero entropy at absolute zero. It is also possible for the highest excited state to have absolute zero te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Configuration Interaction
Configuration interaction (CI) is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, ''configuration'' simply describes the linear combination of Slater determinants used for the wave function. In terms of a specification of orbital occupation (for instance, (1s)2(2s)2(2p)1...), ''interaction'' means the mixing (interaction) of different electronic configurations (states). Due to the long CPU time and large memory required for CI calculations, the method is limited to relatively small systems. In contrast to the Hartree–Fock method, in order to account for electron correlation, CI uses a variational wave function that is a linear combination of configuration state functions (CSFs) built from spin orbitals (denoted by the superscript ''SO''), : \Psi = \sum_ c_ \Phi_^ = c_0\Phi_0^ + c_1\Phi_1^ + where Ψ i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
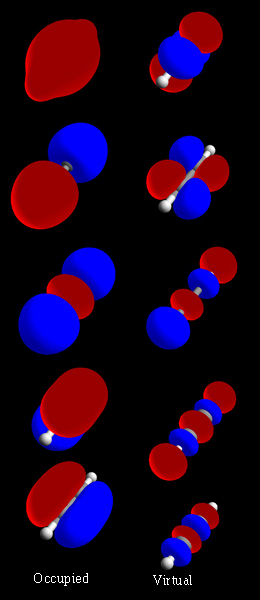
Molecular Orbital
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude. In an isolated atom, the orbital electrons' location is determined by functions called atomic orbitals. When multiple atoms combine chemically into a molecule, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an approximate solution to the Schrödi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |