|
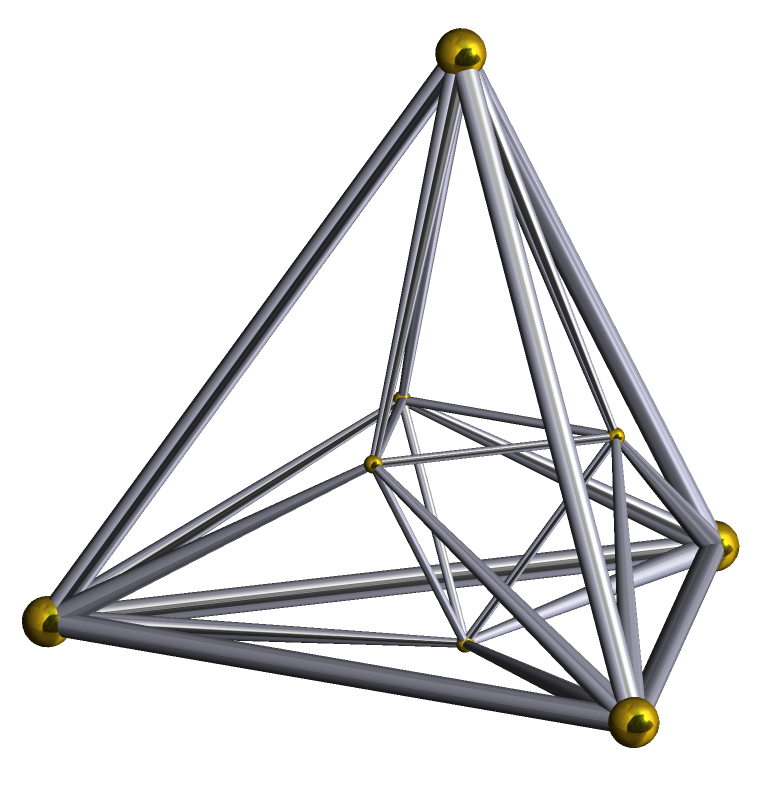
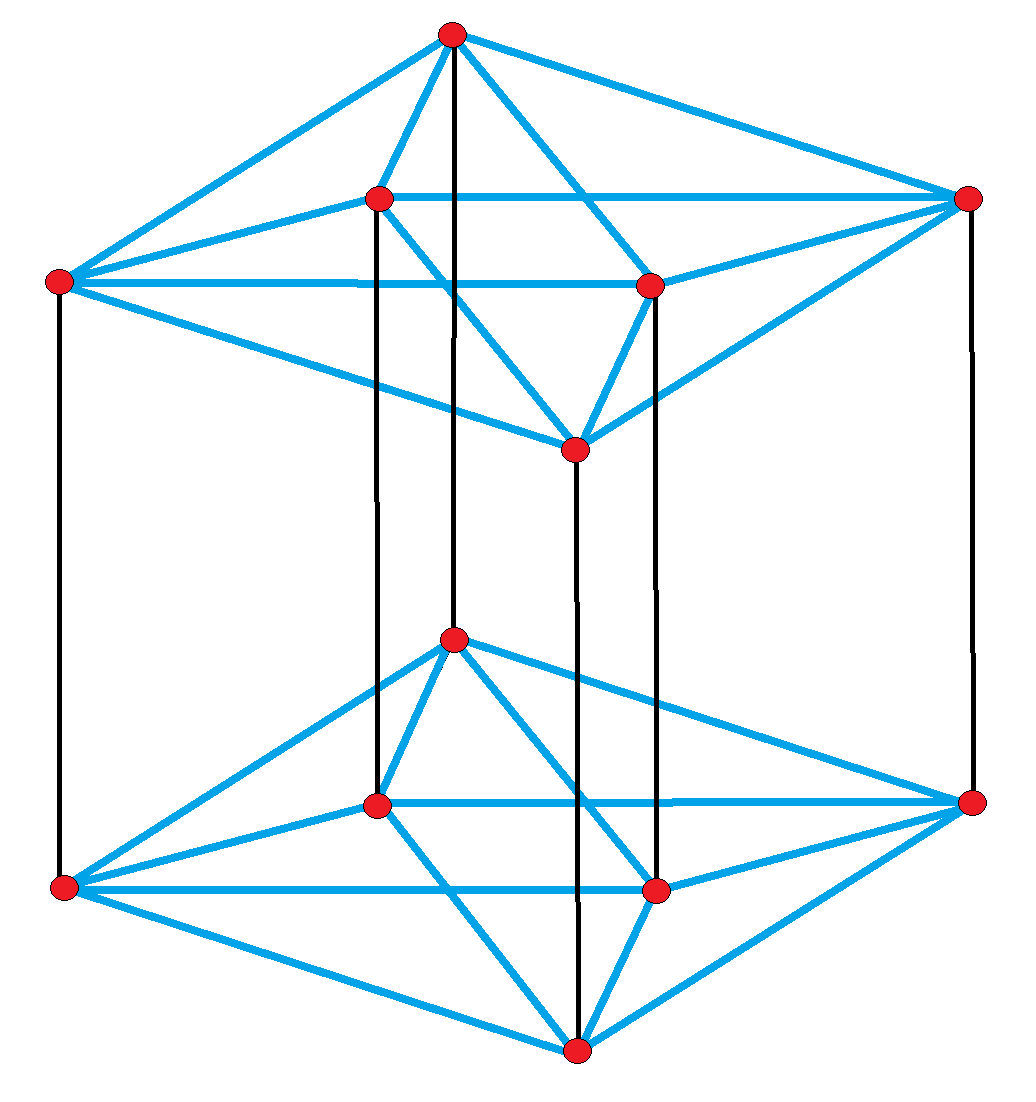
Quarter Tesseractic Honeycomb
In four-dimensional Euclidean geometry, the rectified tesseractic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 4-space. It is constructed by a rectification of a tesseractic honeycomb which creates new vertices on the middle of all the original edges, rectifying the cells into rectified tesseracts, and adding new 16-cell facets at the original vertices. Its vertex figure is an octahedral prism, ×. It is also called a quarter tesseractic honeycomb since it has half the vertices of the 4-demicubic honeycomb, and a quarter of the vertices of a tesseractic honeycomb.Coxeter, Regular and Semi-Regular Polytopes III, (1988), p318 Related honeycombs See also Regular and uniform honeycombs in 4-space: *Tesseractic honeycomb * Demitesseractic honeycomb * 24-cell honeycomb * Truncated 24-cell honeycomb * Snub 24-cell honeycomb * 5-cell honeycomb * Truncated 5-cell honeycomb In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-honeycomb
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets. The complete set of convex uniform 5-polytopes has not been determined, but many can be made as Wythoff constructions from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter diagrams. History of discovery *Regular polytopes: (convex faces) **1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 3 regular polytopes in 5 or more dimensions. *Convex semiregular polytopes: (Various definitions before Coxeter's uniform category) **1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular facets (convex regular 4-polytopes) in his publication ''On the Regular and Semi-Regular Figures in Space of n Dimensions''. *Convex uniform polytopes: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedral Prism
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms. Alternative names *Octahedral dyadic prism ( Norman W. Johnson) *Ope (Jonathan Bowers, for octahedral prism) *Triangular antiprismatic prism *Triangular antiprismatic hyperprism Coordinates It is a Hanner polytope with vertex coordinates, permuting first 3 coordinates: :( �1,0,0 ±1) Structure The octahedral prism consists of two octahedra connected to each other via 8 triangular prisms. The triangular prisms are joined to each other via their square faces. Projections The octahedron-first orthographic projection of the octahedral prism into 3D space has an octahedral envelope. The two octahedral cells project onto the entire volume of this envelope, while the 8 triangular prismic cells project onto its 8 triangular faces. The triangular-prism-first orthographic projection of the octahedral prism into 3D space has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulo
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the '' modulus'' of the operation). Given two positive numbers and , modulo (often abbreviated as ) is the remainder of the Euclidean division of by , where is the dividend and is the divisor. For example, the expression "5 mod 2" would evaluate to 1, because 5 divided by 2 has a quotient of 2 and a remainder of 1, while "9 mod 3" would evaluate to 0, because 9 divided by 3 has a quotient of 3 and a remainder of 0; there is nothing to subtract from 9 after multiplying 3 times 3. Although typically performed with and both being integers, many computing systems now allow other types of numeric operands. The range of values for an integer modulo operation of is 0 to inclusive ( mod 1 is always 0; is undefined, possibly resulting in a division by zero error in some programming languages). See Modular arithmetic for an older and related ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-demicubic Honeycomb
In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of 16-cell facets, three around every face. Its dual is the 24-cell honeycomb. Its vertex figure is a 24-cell. The vertex arrangement is called the B4, D4, or F4 lattice. Alternate names * Hexadecachoric tetracomb/honeycomb * Demitesseractic tetracomb/honeycomb Coordinates Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even. D4 lattice The vertex arrangement of the 16-cell honeycomb is called the D4 lattice or F4 lattice. The vertices of this lattice are the centers of the 3-spheres in the densest known packing of equal spheres in 4-space; its kissing number is 24, which is also the same as the kissing number in R4, as proved by Oleg Musin in 2003. The related D lattice (also called D) can be constructed by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off. Definitions Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tilings or, by extension, to space-filling tessellation with polytope cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges connected to the vertex. The cut surface is the vertex figure. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Tesseract
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope (4-dimensional polytope) bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract. It has two uniform constructions, as a ''rectified 8-cell'' r and a cantellated demitesseract, rr, the second alternating with two types of tetrahedral cells. E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC8. Construction The rectified tesseract may be constructed from the tesseract by truncating its vertices at the midpoints of its edges. The Cartesian coordinates of the vertices of the rectified tesseract with edge length 2 is given by all permutations of: :(0,\ \pm\sqrt,\ \pm\sqrt,\ \pm\sqrt) Images Projections In the cuboctahedron-first parallel projection of the rectified tesseract into 3-dimensional space, the image has the following layout: * The projection envelope is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tesseractic Honeycomb
In four-dimensional euclidean geometry, the tesseractic honeycomb is one of the three regular space-filling tessellations (or honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensional packing of tesseract facets. Its vertex figure is a 16-cell. Two tesseracts meet at each cubic cell, four meet at each square face, eight meet on each edge, and sixteen meet at each vertex. It is an analog of the square tiling, , of the plane and the cubic honeycomb, , of 3-space. These are all part of the hypercubic honeycomb family of tessellations of the form . Tessellations in this family are Self-dual. Coordinates Vertices of this honeycomb can be positioned in 4-space in all integer coordinates (i,j,k,l). Sphere packing Like all regular hypercubic honeycombs, the tesseractic honeycomb corresponds to a sphere packing of edge-length-diameter spheres centered on each vertex, or (dually) inscribed in each cell instead. In the hypercubic honeycomb of 4 dimensions, ver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectification (geometry)
In Euclidean geometry, rectification, also known as critical truncation or complete-truncation, is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points. The resulting polytope will be bounded by vertex figure facets and the rectified facets of the original polytope. A rectification operator is sometimes denoted by the letter with a Schläfli symbol. For example, is the rectified cube, also called a cuboctahedron, and also represented as \begin 4 \\ 3 \end. And a rectified cuboctahedron is a rhombicuboctahedron, and also represented as r\begin 4 \\ 3 \end. Conway polyhedron notation uses for ambo as this operator. In graph theory this operation creates a medial graph. The rectification of any regular self-dual polyhedron or tiling will result in another regular polyhedron or tiling with a tiling order of 4, for example the tetrahedron becoming an octahedron As a special case, a square tiling will ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or '' close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries. A periodic tiling has a repeating pattern. Some special kinds include ''regular tilings'' with regular polygonal tiles all of the same shape, and ''semiregular tilings'' with regular tiles of more than one shape and with every corner identically arranged. The patterns formed by periodic tilings can be categorized into 17 wallpaper groups. A tiling that lacks a repeating pattern is called "non-periodic". An ''aperiodic tiling'' uses a small set of tile shapes that cannot form a repeating pattern. A ''tessellation of space'', also known as a space filling or honeycomb, can be defined in the geometry of higher dimensions. A real physical tessellation is a tiling made of materials such as cemented ceramic squares or hexagons. Such t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions ( theorems) from these. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logical system in which each result is '' proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory, explained in geometrical language. For more than two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |