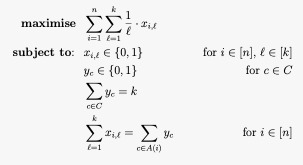|
Proportional Approval Voting
Proportional approval voting (PAV) is a proportional electoral system for selecting committees. It is an extension of the D'Hondt method of apportionment that additionally allows for personal votes (voters vote for candidates, not for a party list). The voters vote via approval ballots where each voter marks those candidates that the voter finds acceptable. History The system was first proposed by Thorvald N. Thiele. It was used in combination with ranked voting in the early 20th century in Sweden, for example between 1909 and 1921 for distributing seats within parties, and in local elections. After 1921 it was replaced by Phragmén's rules. PAV was rediscovered by Forest Simmons in 2001 who gave it the name "proportional approval voting". Definition PAV selects a committee of a fixed desired size with the highest score, where scores are calculated according to the following formula. Given a committee W, for each voter we check how many candidates in the committee the voter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Proportional Approval Voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Proposed by Danish statistician Thorvald N. Thiele in the early 1900s, it was used (with adaptations for party lists) in Sweden for a short period from 1909-1921, and was replaced by a cruder "party-list" style system as it was easier to calculate. Description Sequential Proportional Approval Voting (SPAV) uses Approval Voting ballots to elect multiple winners equitably by selecting a candidate in each round and then reweighing the approvals for the subsequent rounds. Each ballot is assigned a value equal to the reciprocal of one more than the number of candidates approved on that ballot who have been designated as elected. Each ballot is counted at its current value as a vote for all continuing candidates approved on that ballot. The candid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Justified Representation
Justified representation (JR) is a criterion for evaluating the fairness of electoral systems in multiwinner voting, particularly in multiwinner approval voting. It can be seen as an adaptation of the proportional representation criterion to approval voting. Definitions One definition for "proportional representation" is that the candidates are partitioned into disjoint parties, and each voter approves all candidates in a single party. For example, suppose we need to elect a committee of size 10. Suppose that exactly 50% of the voters approve all candidates in party A, exactly 30% approve all candidates in party B, and exactly 20% approve all candidates in party C. Then, proportional representation requires that the committee contains exactly 5 candidates from party A, exactly 3 candidates from party B, and exactly 2 candidates from party C. If the fractions are not exact, then some rounding method should be used, and this can be done by various apportionment methods. However, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Linear Programming
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are linear. Integer programming is NP-complete. In particular, the special case of 0-1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp's 21 NP-complete problems. If some decision variables are not discrete, the problem is known as a mixed-integer programming problem. Canonical and standard form for ILPs In integer linear programming, the ''canonical form'' is distinct from the ''standard form''. An integer linear program in canonical form is expressed thus (note that it is the \mathbf vector which is to be decided): : \begin & \text && \mathbf^\mathrm \mathbf\\ & \text && A \mathbf \le \mathbf, \\ & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Programming
An integer programming problem is a mathematical optimization or Constraint satisfaction problem, feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are Linear function (calculus), linear. Integer programming is NP-complete. In particular, the special case of 0-1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp's 21 NP-complete problems. If some decision variables are not discrete, the problem is known as a mixed-integer programming problem. Canonical and standard form for ILPs In integer linear programming, the ''canonical form'' is distinct from the ''standard form''. An integer linear program in canonical form is expressed thus (note that it is the \mathbf vector which is to be decided): : \begin & \text && \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-hard
In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard problem is the subset sum problem. A more precise specification is: a problem ''H'' is NP-hard when every problem ''L'' in NP can be reduced in polynomial time to ''H''; that is, assuming a solution for ''H'' takes 1 unit time, ''H''s solution can be used to solve ''L'' in polynomial time. As a consequence, finding a polynomial time algorithm to solve any NP-hard problem would give polynomial time algorithms for all the problems in NP. As it is suspected that P≠NP, it is unlikely that such an algorithm exists. It is suspected that there are no polynomial-time algorithms for NP-hard problems, but that has not been proven. Moreover, the class P, in which all problems can be solved in polynomial time, is contained in the NP class. Defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Proportional Approval Voting
Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. Proposed by Danish statistician Thorvald N. Thiele in the early 1900s, it was used (with adaptations for party lists) in Sweden for a short period from 1909-1921, and was replaced by a cruder "party-list" style system as it was easier to calculate. Description Sequential Proportional Approval Voting (SPAV) uses Approval Voting ballots to elect multiple winners equitably by selecting a candidate in each round and then reweighing the approvals for the subsequent rounds. Each ballot is assigned a value equal to the reciprocal of one more than the number of candidates approved on that ballot who have been designated as elected. Each ballot is counted at its current value as a vote for all continuing candidates approved on that ballot. The candid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
House Monotonicity
House monotonicity (also called house-size monotonicity) is a property of apportionment methods and multiwinner voting systems. These are methods for allocating seats in a parliament among federal states (or among political party). The property says that, if the number of seats in the "house" (the parliament) increases, and the method is re-activated, then no state should have less seats than it previously had. A method that fails to satisfy house-monotonicity is said to have the Alabama paradox. House monotonicity is the special case of ''resource monotonicity'' for the setting in which the resource consists of identical discrete items (the seats). Methods violating house-monotonicity An example of a method violating house-monotonicity is the largest remainder method (= Hamilton's method). Consider the following instance with three states: When one seat is added to the house, the share of state C decreases from 2 to 1. This occurs because increasing the number of seats increas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consistency Criterion
A voting system is consistent if, whenever the electorate is divided (arbitrarily) into several parts and elections in those parts garner the same result, then an election of the entire electorate also garners that result. Smith calls this property separability and Woodall calls it convexity. It has been proven a ranked voting system is "consistent if and only if it is a scoring function", i.e. a positional voting system. Borda count is an example of this. The failure of the consistency criterion can be seen as an example of Simpson's paradox Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science st .... As shown below under Kemeny-Young, passing or failing the consistency criterion can depend on whether the election selects a single winner or a full ranking of the candidates (sometimes refe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Method Of Equal Shares
The Method of Equal Shares (in early papers the method has been also referred to as Rule X, but since 2022 the authors started using the name "method of equal shares") is a proportional method of counting ballots that applies to participatory budgeting to committee elections and to simultaneous public decisions. It can be used, when the voters vote via approval ballots, ranked ballots or cardinal ballots. If each voter has equal entitlement and each voter submits approval preferences, the Method of Equal Shares is a specific rule in a more general class of rules called PB-EAR that was designed earlier in 2019 by Aziz and Lee for ordinal preferences (that include approval ballots). Motivation The method is an alternative to the knapsack algorithm which is used by most cities even though it is a disproportional method. For example, if 51% of the population support 10 red projects and 49% support 10 blue projects, and the money suffices only for 10 projects, the knapsack budge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |