|
Planigon
In geometry, a planigon is a convex polygon that can fill the plane with only copies of itself (Homotopy#Isotopy, isotopic to the Prototile, fundamental units of Monohedral tiling, monohedral tessellations). In the Euclidean plane there are 3 regular planigons; equilateral triangle, squares, and regular hexagons; and 8 List of Euclidean uniform tilings, semiregular planigons; and 4 Euclidean_tilings_by_convex_regular_polygons, demiregular planigons which can tile the plane only with other planigons. All angles of a planigon are whole divisors of 360°. Tilings are made by edge-to-edge connections by perpendicular bisectors of the edges of the original uniform lattice, or centroids along common edges (they coincide). Tilings made from planigons can be seen as Dual polyhedron, dual tilings to the List of Euclidean uniform tilings, regular, semiregular, and Euclidean_tilings_by_convex_regular_polygons, demiregular tilings of the plane by regular polygons. History In the 1987 book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Euclidean Uniform Tilings
This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane, and their dual tilings. There are three regular and eight semiregular tilings in the plane. The semiregular tilings form new tilings from their duals, each made from one type of irregular face. John Conway calls these uniform duals ''Catalan tilings'', in parallel to the Catalan solid polyhedra. Uniform tilings are listed by their vertex configuration, the sequence of faces that exist on each vertex. For example ''4.8.8'' means one square and two octagons on a vertex. These 11 uniform tilings have 32 different ''uniform colorings''. A uniform coloring allows identical sided polygons at a vertex to be colored differently, while still maintaining vertex-uniformity and transformational congruence between vertices. (Note: Some of the tiling images shown below are ''not'' color-uniform) In addition to the 11 convex uniform tilings, there are also 14 known nonconvex tilings, using star ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereohedron
In geometry and crystallography, a stereohedron is a convex polyhedron that fills space isohedrally, meaning that the symmetries of the tiling take any copy of the stereohedron to any other copy. Two-dimensional analogues to the stereohedra are called planigons. Higher dimensional polytopes can also be stereohedra, while they would more accurately be called stereotopes. Plesiohedra A subset of stereohedra are called plesiohedrons, defined as the Voronoi cells of a symmetric Delone set. Parallelohedrons are plesiohedra which are space-filling by translation only. Edges here are colored as parallel vectors. Other periodic stereohedra The catoptric tessellation contain stereohedra cells. Dihedral angles are integer divisors of 180°, and are colored by their order. The first three are the fundamental domains of _3, _3, and _3 symmetry, represented by Coxeter-Dynkin diagrams: , and . _3 is a half symmetry of _3, and _3 is a quarter symmetry. Any space-filling stereohedra wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
All Planigons
All or ALL may refer to: Language * All, an indefinite pronoun in English * All, one of the English determiners * Allar language (ISO 639-3 code) * Allative case (abbreviated ALL) Music * All (band), an American punk rock band * ''All'' (All album), 1999 * ''All'' (Descendents album) or the title song, 1987 * ''All'' (Horace Silver album) or the title song, 1972 * ''All'' (Yann Tiersen album), 2019 * "All" (song), by Patricia Bredin, representing the UK at Eurovision 1957 * "All (I Ever Want)", a song by Alexander Klaws, 2005 * "All", a song by Collective Soul from ''Hints Allegations and Things Left Unsaid'', 1994 Science and mathematics * ALL (complexity), the class of all decision problems in computability and complexity theory * Acute lymphoblastic leukemia * Anterolateral ligament Sports * American Lacrosse League * Arena Lacrosse League, Canada * Australian Lacrosse League Other uses * All, Missouri, a community in the United States * All, a brand of Sun Products * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fritz Laves
Fritz Henning Emil Paul Berndt Laves (27 February 1906 – 12 August 1978) was a German crystallographer who served as the president of the German Mineralogical Society from 1956 to 1958. He is the namesake of Laves phases and the Laves tilings; the Laves graph, a highly-symmetrical three-dimensional crystal structure that he studied, was named after him by H. S. M. Coxeter. Education and career Laves was born in Hanover, the son of a judge and the great-grandson of architect Georg Ludwig Friedrich Laves. He grew up in Göttingen, where his interests included piano music as well as collecting rocks and minerals. He began his university studies in geology in 1924 at the University of Innsbruck, and continued at the University of Göttingen before moving to ETH Zurich for doctoral studies under Paul Niggli. In 1929 he took a faculty position under Victor Goldschmidt at Göttingen. He tried unsuccessfully to prevent Goldschmidt from being dismissed in 1933, and later had difficul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bisection
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes through the midpoint of a given segment) and the ''angle bisector'' (a line that passes through the apex of an angle, that divides it into two equal angles). In three-dimensional space, bisection is usually done by a plane (geometry), plane, also called the ''bisector'' or ''bisecting plane''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line, which meets the segment at its midpoint perpendicularly. The Horizontal intersector of a segment AB also has the property that each of its points X is equidistant from the segment's endpoints: (D)\quad , XA, = , XB, . The proof follows from and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^2=, XB, ^2 \; . Property (D) is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetries and n reflection symmetries. Usually, we take n \ge 3 here. The associated rotations and reflections make up the dihedral group \mathrm_n. If n is odd, each axis of symmetry connects the midpoint of one side to the opposite vertex. If n is even, there are n/2 axes of symmetry connecting the midpoints of opposite sides and n/2 axes of symmetry connecting oppo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in ''n''-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the ''barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a ''center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" is of recent coinage (1814). It is used as a substitute for the older te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex polygon, convex, star polygon, star or Skew polygon, skew. In the limit (mathematics), limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon (effectively a Line (geometry), straight line), if the edge length is fixed. General properties ''These properties apply to all regular polygons, whether convex or star polygon, star.'' A regular ''n''-sided polygon has rotational symmetry of order ''n''. All vertices of a regular polygon lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the property of equal-length sides, this implies that every regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Tilings By Convex Regular Polygons
Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his ''Harmonices Mundi'' (Latin: ''The Harmony of the World'', 1619). Notation of Euclidean tilings Euclidean tilings are usually named after Cundy & Rollett’s notation. This notation represents (i) the number of vertices, (ii) the number of polygons around each vertex (arranged clockwise) and (iii) the number of sides to each of those polygons. For example: 36; 36; 34.6, tells us there are 3 vertices with 2 different vertex types, so this tiling would be classed as a ‘3-uniform (2-vertex types)’ tiling. Broken down, 36; 36 (both of different transitivity class), or (36)2, tells us that there are 2 vertices (denoted by the superscript 2), each with 6 equilateral 3-sided polygons (triangles). With a final vertex 34.6, 4 more contiguous equilateral triangles and a single regular hexagon. However, this notation has two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solids
In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids (which are composed of only one type of polygon), excluding the prisms and antiprisms, and excluding the pseudorhombicuboctahedron. They are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices. "Identical vertices" means that each two vertices are symmetric to each other: A global isometry of the entire solid takes one vertex to the other while laying the solid directly on its initial position. observed that a 14th polyhedron, the elongated square gyrobicupola (or pseudo-rhombicuboctahedron), meets a weaker definition of an Archimedean solid, in which "identical vertices" means merely that the faces surrounding each vertex are of the same types (i.e. each vertex looks the same from close up), so only a loca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
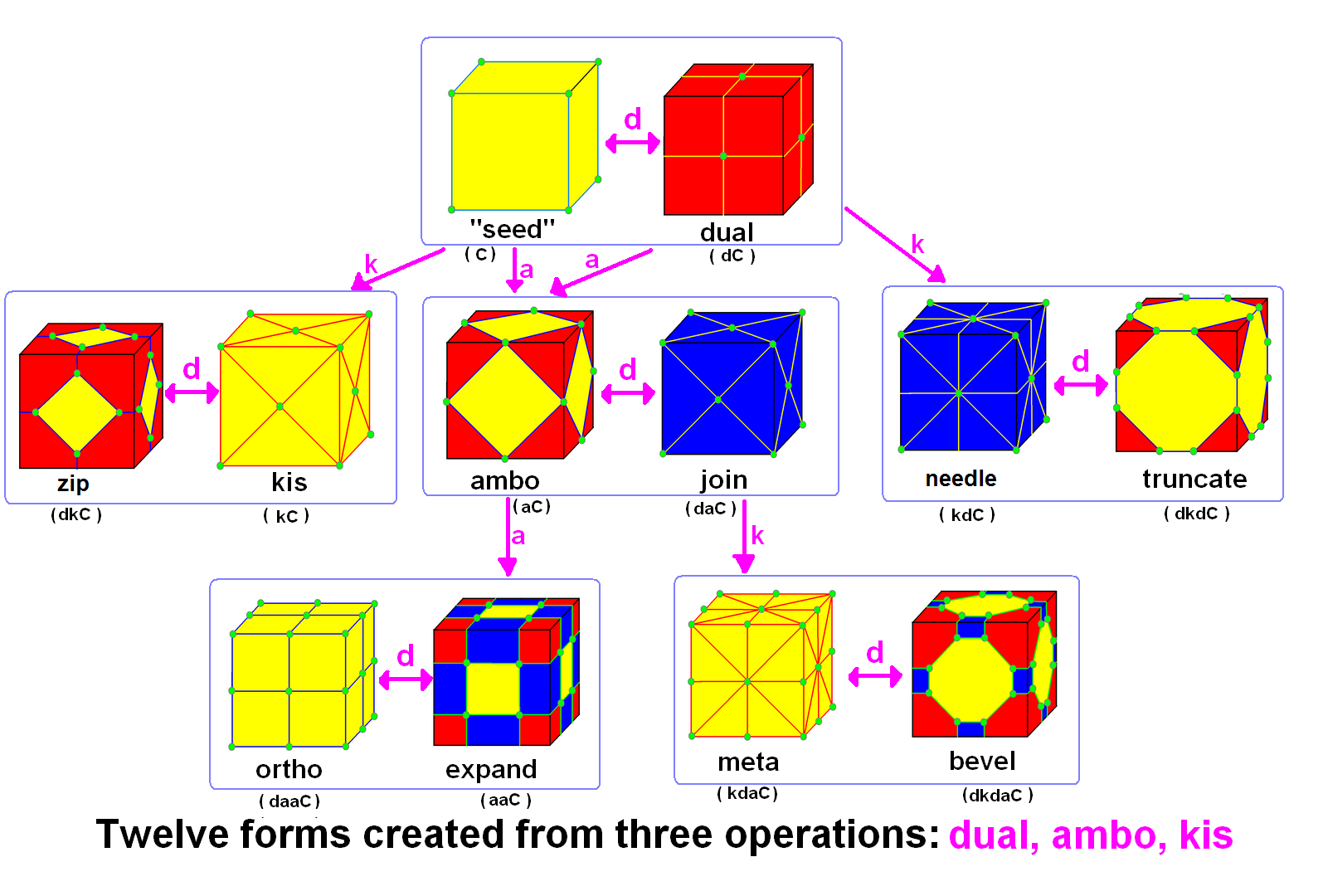
Conway Polyhedron Notation
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), (snub), and (truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the Archimedean and Catal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face Configuration
In geometry, a vertex configurationCrystallography of Quasicrystals: Concepts, Methods and Structures by Walter Steurer, Sofia Deloudi, (2009) pp. 18–20 and 51–53Physical Metallurgy: 3-Volume Set, Volume 1 edited by David E. Laughlin, (2014) pp. 16–20 is a shorthand notation for representing the of a or |