|
Post-Newtonian Approximation
In general relativity, post-Newtonian expansions (PN expansions) are used for finding an approximate solution of Einstein field equations for the metric tensor. The approximations are expanded in small parameters that express orders of deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields sometimes it is preferable to solve the complete equations numerically. This method is a common mark of effective field theories. In the limit, when the small parameters are equal to 0, the post-Newtonian expansion reduces to Newton's law of gravity. Expansion in 1/''c''2 The post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter that creates the gravitational field, to the speed of light, which in this case is more precisely called the '' speed of gravity''. In the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GR2bodyparameterspace
GR may refer to: Arts and entertainment Film and television * ''Golmaal Returns'', a Hindi comedy film * ''Generator Rex'', an animated sci-fi series * Guilty Remnant, a fictional cult in The Leftovers (TV series), ''The Leftovers'' (TV series) Music * ''Ghost Reveries'', a 2005 album by Opeth *Good Riddance (band), an American punk group Review websites * ''GameRevolution'', run by Mandatory * ''GamesRadar+'', run by Future plc * GoodReads, run by Amazon Video games * ''Tom Clancy's Ghost Recon'', a tactical shooter series Government and politics * ''Georgius Rex'' (royal cypher: GR); see King George (other) ** George VI of the United Kingdom ** George V of the United Kingdom * Globalise Resistance, a British anti-capitalist group * Gonnema Regiment of the South African Army * Government relations, or lobbying * Government Resident, a diplomatic post Places Country * Greece (ISO 3166/NATO:GR) Cities *Grand Rapids, Michigan *Grand Rapids, Minnesota Regions * Giurgiu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Space
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model. The model helps show how a spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Mathematician Hermann Minkowski developed it from the work of Hendrik Lorentz, Henri Poincaré, and others said it "was grown on experimental physical grounds". Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure by which special relativity is formalized. While the individual components in Euclidean space and time might differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total interval in spacetime between events.This makes spacetime distance an inva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PNAS
''Proceedings of the National Academy of Sciences of the United States of America'' (often abbreviated ''PNAS'' or ''PNAS USA'') is a peer-reviewed multidisciplinary scientific journal. It is the official journal of the National Academy of Sciences, published since 1915, and publishes original research, scientific reviews, commentaries, and letters. According to '' Journal Citation Reports'', the journal has a 2022 impact factor of 9.4. ''PNAS'' is the second most cited scientific journal, with more than 1.9 million cumulative citations from 2008 to 2018. In the past, ''PNAS'' has been described variously as "prestigious", "sedate", "renowned" and "high impact". ''PNAS'' is a delayed open-access journal, with an embargo period of six months that can be bypassed for an author fee ( hybrid open access). Since September 2017, open access articles are published under a Creative Commons license. Since January 2019, ''PNAS'' has been online-only, although print issues are avail ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameterized Post-Newtonian Formalism
In physics, precisely in the study of the theory of general relativity and many alternatives to it, the post-Newtonian formalism is a calculational tool that expresses Einstein's (nonlinear) equations of gravity in terms of the lowest-order deviations from Newton's law of universal gravitation. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher-order terms can be added to increase accuracy, but for strong fields, it may be preferable to solve the complete equations numerically. Some of these post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter forming the gravitational field to the speed of light, which in this case is better called the speed of gravity. In the limit, when the fundamental speed of gravity becomes infinite, the post-Newtonian expansion reduces to Newton's law of gravity. The parameterized post-Newtonian formalism or PPN formalism, is a version of this fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearized Gravity
In the theory of general relativity, linearized gravity is the application of perturbation theory to the metric tensor that describes the geometry of spacetime. As a consequence, linearized gravity is an effective method for modeling the effects of gravity when the gravitational field is weak. The usage of linearized gravity is integral to the study of gravitational waves and weak-field gravitational lensing. Weak-field approximation The Einstein field equation (EFE) describing the geometry of spacetime is given as : R_ - \fracRg_ = \kappa T_ where R_ is the Ricci tensor, R is the Ricci scalar, T_ is the energy–momentum tensor, \kappa = 8 \pi G / c^4 is the Einstein gravitational constant, and g_ is the spacetime metric tensor that represents the solutions of the equation. Although succinct when written out using Einstein notation, hidden within the Ricci tensor and Ricci scalar are exceptionally nonlinear dependencies on the metric tensor that render the prospect of fin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein–Infeld–Hoffmann Equations
The Einstein–Infeld–Hoffmann equations of motion, jointly derived by Albert Einstein, Leopold Infeld and Banesh Hoffmann, are the differential equations describing the approximate dynamics of a system of point-like masses due to their mutual gravitational interactions, including general relativistic effects. It uses a first-order post-Newtonian expansion and thus is valid in the limit where the velocities of the bodies are small compared to the speed of light and where the gravitational fields affecting them are correspondingly weak. Given a system of ''N'' bodies, labelled by indices ''A'' = 1, ..., ''N'', the barycentric acceleration vector of body ''A'' is given by: : \begin \vec_A & = \sum_ \frac \\ & \quad + \frac \sum_ \frac \left v_A^2+2v_B^2 - 4( \vec_A \cdot \vec_B) - \frac ( \vec_ \cdot \vec_B)^2 \right. \\ & \qquad \left. - 4 \sum_ \frac - \sum_ \frac + \frac( (\vec_B-\vec_A) \cdot \vec_B ) \right\\ & \qua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate Conditions
In general relativity, the laws of physics can be expressed in a generally covariant form. In other words, the description of the world as given by the laws of physics does not depend on our choice of coordinate systems. However, it is often useful to fix upon a particular coordinate system, in order to solve actual problems or make actual predictions. A coordinate condition selects such coordinate system(s). Indeterminacy in general relativity The Einstein field equations do not determine the metric uniquely, even if one knows what the metric tensor equals everywhere at an initial time. This situation is analogous to the failure of the Maxwell equations to determine the potentials uniquely. In both cases, the ambiguity can be removed by gauge fixing. Thus, coordinate conditions are a type of gauge condition. No coordinate condition is generally covariant, but many coordinate conditions are Lorentz covariant or rotationally covariant. Naively, one might think that coordinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hubble's Law
Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther a galaxy is from the Earth, the faster it moves away. A galaxy's recessional velocity is typically determined by measuring its redshift, a shift in the frequency of light emitted by the galaxy. The discovery of Hubble's law is attributed to work published by Edwin Hubble in 1929, but the notion of the universe expanding at a calculable rate was first derived from general relativity equations in 1922 by Alexander Friedmann. The Friedmann equations showed the universe might be expanding, and presented the expansion speed if that were the case. Before Hubble, astronomer Carl Wilhelm Wirtz had, in 1922 and 1924, deduced with his own data that galaxies that appeared smaller and dimmer had larger redshifts and thus that more distant galaxies recede faster from the observer. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D'Alembert Operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator (denoted by a box: \Box), also called the d'Alembertian, wave operator, box operator or sometimes quabla operator (''cf''. nabla symbol) is the Laplace operator of Minkowski space. The operator is named after French mathematician and physicist Jean le Rond d'Alembert. In Minkowski space, in standard coordinates , it has the form : \begin \Box & = \partial^\mu \partial_\mu = \eta^ \partial_\nu \partial_\mu = \frac \frac - \frac - \frac - \frac \\ & = \frac - \nabla^2 = \frac - \Delta ~~. \end Here \nabla^2 := \Delta is the 3-dimensional Laplacian and is the inverse Minkowski metric with :\eta_ = 1, \eta_ = \eta_ = \eta_ = -1, \eta_ = 0 for \mu \neq \nu. Note that the and summation indices range from 0 to 3: see Einstein notation. (Some authors alternatively use the negative metric signature of , with \eta_ = -1,\; \eta_ = \eta_ = \eta_ = 1.) Lorentz transformations leave the Mi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Wave
Gravitational waves are oscillations of the gravitational field that Wave propagation, travel through space at the speed of light; they are generated by the relative motion of gravity, gravitating masses. They were proposed by Oliver Heaviside in 1893 and then later by Henri Poincaré in 1905 as the gravitational equivalent of Electromagnetic radiation, electromagnetic waves. In 1916, Albert Einstein demonstrated that gravitational waves result from his general theory of relativity as ripples in spacetime. Gravitational waves transport energy as gravitational radiation, a form of radiant energy similar to electromagnetic radiation. Newton's law of universal gravitation, part of classical mechanics, does not provide for their existence, instead asserting that gravity has instantaneous effect everywhere. Gravitational waves therefore stand as an important relativistic phenomenon that is absent from Newtonian physics. Gravitational-wave astronomy has the advantage that, unlike elec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
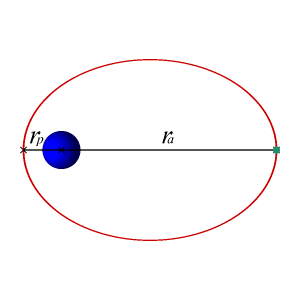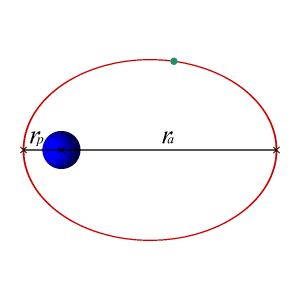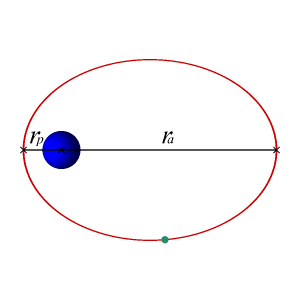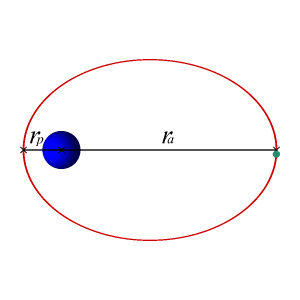
Two-body Problem In General Relativity
The two-body problem in general relativity (or relativistic two-body problem) is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of light by gravity and the motion of a planet orbiting its sun. Solutions are also used to describe the motion of binary stars around each other, and estimate their gradual loss of energy through gravitational radiation. General relativity describes the gravitational field by curved space-time; the field equations governing this curvature are nonlinear and therefore difficult to solve in a closed form. No exact solutions of the Kepler problem have been found, but an approximate solution has: the Schwarzschild solution. This solution pertains when the mass ''M'' of one body is overwhelmingly greater than the mass ''m'' of the other. If so, the larger mass may be taken as stationary and the sole contributor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |