|
Planimeter
A planimeter, also known as a platometer, is a measuring instrument used to determine the area of an arbitrary two-dimensional shape. Construction There are several kinds of planimeters, but all operate in a similar way. The precise way in which they are constructed varies, with the main types of mechanical planimeter being polar, linear, and Prytz or "hatchet" planimeters. The Swiss mathematician Jakob Amsler-Laffon built the first modern planimeter in 1854, the concept having been pioneered by Johann Martin Hermann in 1818. Many developments followed Amsler's famous planimeter, including electronic versions. The Amsler (polar) type consists of a two-bar linkage. At the end of one link is a pointer, used to trace around the boundary of the shape to be measured. The other end of the linkage pivots freely on a weight that keeps it from moving. Near the junction of the two links is a measuring wheel of calibrated diameter, with a scale to show fine rotation, and worm gearing for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvimeter
An opisometer, also called a curvimeter, meilograph, or map measurer, is an instrument for measurement, measuring the lengths of arbitrary curved lines. Explanation A simple opisometer consists of a toothed wheel of known circumference on a handle. The wheel is placed in contact with the curved line to be measured and run along its length. By counting the number of teeth passing a mark on the handle while this is done, the length of the line can be ascertained: :line length = wheel circumference × teeth counted/teeth on wheel. In more sophisticated models, sometimes called a chartometer, the wheel is connected via gearing to a rotary dial from which the line length can be directly read. The instrument is most commonly used to measure the lengths of roads, rivers and other line features on maps. Opisometers designed for this purpose provide scales reading the measured distance in kilometers and miles. History of the opisometer Early versions of this instrument were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensional Instruments
A ''measuring instrument'' is a device to measurement, measure a physical quantity. In the physical sciences, quality assurance, and engineering, ''measurement'' is the activity of obtaining and comparing physical quantity, physical quantities of real-world physical object, objects and phenomenon, events. Established standard objects and events are used as unit of measurement, ''units'', and the process of measurement gives a number relating the item under study and the referenced unit of measurement. Measuring instruments, and formal test methods which define the instrument's use, are the means by which these relations of numbers are obtained. All measuring instruments are subject to varying degrees of instrument error and measurement uncertainty. These instruments may range from simple objects such as rulers and stopwatches to electron microscopes and particle accelerators. Virtual instrumentation is widely used in the development of modern measuring instruments. Time In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shoelace Formula
The shoelace formula, also known as Gauss's area formula and the surveyor's formula, is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their Cartesian coordinates in the plane. It is called the shoelace formula because of the constant cross-multiplying for the coordinates making up the polygon, like threading shoelaces. It has applications in surveying and forestry,Hans Pretzsch, Forest Dynamics, Growth and Yield: From Measurement to Model', Springer, 2009, , p. 232. among other areas. The formula was described by Albrecht Ludwig Friedrich Meister (1724–1788) in 1769 and is based on the trapezoid formula which was described by Carl Friedrich Gauss and Carl Gustav Jacob Jacobi, C.G.J. Jacobi. The triangle form of the area formula can be considered to be a special case of Green's theorem. The area formula can also be applied to self-overlapping polygons since the meaning of area is still clear even though self-overlapping polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
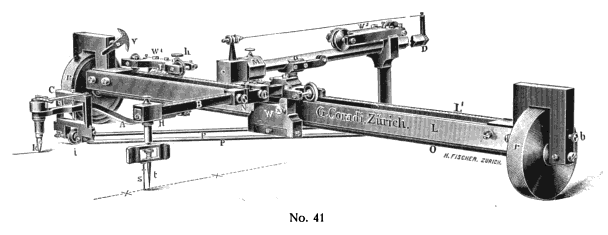
Integraph
An Integraph is a mechanical analog computing device for plotting the integral of a graphically defined function. History Gaspard-Gustave de Coriolis first described the fundamental principal of a mechanical integraph in 1836 in the ''Journal de Mathématiques Pures et Appliquées''. A full description of an integraph was published independently around 1880 by both British physicist Sir Charles Vernon Boys and Bruno Abdank-Abakanowicz, a Polish-Lithuanian mathematician/electrical engineer. Boys described a design for an integraph in 1881 in the ''Philosophical Magazine''. Abakanowicz developed a practical working prototype in 1878, with improved versions of the prototype being manufactured by firms such as Coradi in Zürich, Switzerland. Customized and further improved versions of Abakanowicz's design were manufactured until well after 1900, with these later modifications being made by Abakanowicz in collaboration M. D. Napoli, the "principal inspector of the railroad Chemi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Green's Theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region (surface in \R^2) bounded by . It is the two-dimensional special case of Stokes' theorem (surface in \R^3). In one dimension, it is equivalent to the fundamental theorem of calculus. In three dimensions, it is equivalent to the divergence theorem. Theorem Let be a positively oriented, piecewise smooth, simple closed curve in a plane, and let be the region bounded by . If and are functions of defined on an open region containing and have continuous partial derivatives there, then \oint_C (L\, dx + M\, dy) = \iint_ \left(\frac - \frac\right) dA where the path of integration along is counterclockwise. Application In physics, Green's theorem finds many applications. One is solving two-dimensional flow integrals, stating that the sum of fluid outflowing from a volume is equal to the total outflow summed about an enclosing area. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Instrument
A mathematical instrument is a tool or device used in the study or practice of mathematics. In geometry, construction of various proofs was done using only a compass and straightedge; arguments in these proofs relied only on idealized properties of these instruments and literal construction was regarded as only an approximation. In applied mathematics, mathematical instruments were used for measuring angles and distances, in astronomy, navigation, surveying and in the measurement of time.Gerard L'Estrange Turner ''Scientific Instruments, 1500-1900: An Introduction'' ( University of California Press, 1998) page 8 Overview Instruments such as the astrolabe, the quadrant, and others were used to measure and accurately record the relative positions and movements of planets and other celestial objects. The sextant and other related instruments were essential for navigation at sea. Most instruments are used within the field of geometry, including the ruler, dividers, protracto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinate System
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates. The polar coordinate system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measuring Instrument
Instrumentation is a collective term for measuring instruments, used for indicating, measuring, and recording physical quantities. It is also a field of study about the art and science about making measurement instruments, involving the related areas of metrology, automation, and control theory. The term has its origins in the art and science of scientific instrument-making. Instrumentation can refer to devices as simple as direct-reading thermometers, or as complex as multi- sensor components of industrial control systems. Instruments can be found in laboratories, refineries, factories and vehicles, as well as in everyday household use (e.g., smoke detectors and thermostats). Measurement parameters Instrumentation is used to measure many parameters (physical values), including: *Pressure, either differential or static * Flow *Temperature * Levels of liquids, etc. *Moisture or humidity *Density *Viscosity * ionising radiation * Frequency * Current *Voltage * Induct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Tools
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a ''proof'' consisting of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstracti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Technical Drawing Tools
Drafting tools may be used for measurement and layout of drawings, or to improve the consistency and speed of creation of standard drawing elements. Tools such as pens and pencils mark the drawing medium. Other tools such as straight edges, assist the operator in drawing straight lines, or assist the operator in drawing complicated shapes repeatedly. Various scales and the protractor are used to measure the lengths of lines and angles, allowing accurate scale drawing to be carried out. The compass is used to draw arcs and circles. A drawing board was used to hold the drawing media in place; later boards included drafting machines that sped the layout of straight lines and angles. Tools such as templates and lettering guides assisted in the drawing of repetitive elements such as circles, ellipses, schematic symbols and text. Other auxiliary tools were used for special drawing purposes or for functions related to the preparation and revision of drawings. The tools used for manual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tanya Leise
Tanya L. Leise (died January 18, 2023) was an American biomathematician specializing in the mathematical modeling of circadian rhythms and related phenomena such as jet lag and hibernation. She was a professor of mathematics at Amherst College. Education and career Leise was a 1993 graduate of Stanford University Leland Stanford Junior University, commonly referred to as Stanford University, is a Private university, private research university in Stanford, California, United States. It was founded in 1885 by railroad magnate Leland Stanford (the eighth .... She went to Texas A&M University for graduate study, completing a Ph.D. there in 1998. Her dissertation, ''An Analog to the Dirichlet-to-Nuemann Map and Its Application to Dynamic Elastic Fracture'', was supervised by Jay R. Walton. After working as a visiting lecturer at Indiana University, she joined the faculty of the Rose–Hulman Institute of Technology in 1999. She moved to Amherst as a visiting assistant professor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |