|
Physical Field
In science, a field is a physical quantity, represented by a scalar, vector, or tensor, that has a value for each point in space and time. An example of a scalar field is a weather map, with the surface temperature described by assigning a number to each point on the map. A surface wind map, assigning an arrow to each point on a map that describes the wind speed and direction at that point, is an example of a vector field, i.e. a 1-dimensional (rank-1) tensor field. Field theories, mathematical descriptions of how field values change in space and time, are ubiquitous in physics. For instance, the electric field is another rank-1 tensor field, while electrodynamics can be formulated in terms of two interacting vector fields at each point in spacetime, or as a single-rank 2-tensor field. In the modern framework of the quantum field theory, even without referring to a test particle, a field occupies space, contains energy, and its presence precludes a classical "true vacuum". ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as the '' gravitational force field'' exerted on another massive body. It has dimension of acceleration (L/T2) and it is measured in units of newtons per kilogram (N/kg) or, equivalently, in meters per second squared (m/s2). In its original concept, gravity was a force between point masses. Following Isaac Newton, Pierre-Simon Laplace attempted to model gravity as some kind of radiation field or fluid, and since the 19th century, explanations for gravity in classical mechanics have usually been taught in terms of a field model, rather than a point attraction. It results from the spatial gradient of the gravitational potential field. In general relativity, rather than two particles attracting each other, the particles distort spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newtonian Gravity
Newton's law of universal gravitation describes gravity as a force by stating that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the " first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors. This is a general physical law derived from empirical observations by what Isaac Newton called ''inductive reasoning''. It is a part of classical mechanics and was formulated in Newton's work ''Philosophiæ Naturalis Principia Mathematica'' (Latin for 'Mathematical Principles of Natural Philosophy' (the ''Principia'')), first published on 5 July 1687. The equation for universal gravitation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
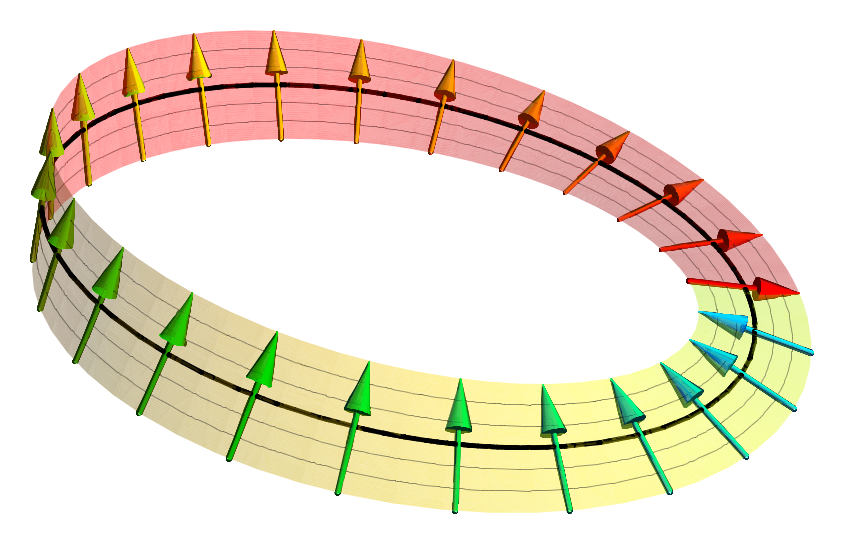
Spinor
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex numbers, complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal transformation, infinitesimal) rotation, but unlike Euclidean vector, geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of Section (fiber bundle), sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scaled to form a vector space. A '' vector quantity'' is a vector-valued physical quantity, including units of measurement and possibly a support, formulated as a '' directed line segment''. A vector is frequently depicted graphically as an arrow connecting an ''initial point'' ''A'' with a ''terminal point'' ''B'', and denoted by \stackrel \longrightarrow. A vector is what is needed to "carry" the point ''A'' to the point ''B''; the Latin word means 'carrier'. It was first used by 18th century astronomers investigating planetary revolution around the Sun. The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from ''A'' to ''B''. Many algebraic operations on real numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (physics)
Scalar quantities or simply scalars are physical quantities that can be described by a single pure number (a ''scalar'', typically a real number), accompanied by a unit of measurement, as in "10cm" (ten centimeters). Examples of scalar are length, mass, charge, volume, and time. Scalars may represent the magnitude of physical quantities, such as speed is to velocity. Scalars do not represent a direction. Scalars are unaffected by changes to a vector space basis (i.e., a coordinate rotation) but may be affected by translations (as in relative speed). A change of a vector space basis changes the description of a vector in terms of the basis used but does not change the vector itself, while a scalar has nothing to do with this change. In classical physics, like Newtonian mechanics, rotations and reflections preserve scalars, while in relativity, Lorentz transformations or space-time translations preserve scalars. The term "scalar" has origin in the multiplication o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor Field
In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space (typically a Euclidean space or manifold) or of the physical space. Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in material object, and in numerous applications in the physical sciences. As a tensor is a generalization of a scalar (a pure number representing a value, for example speed) and a vector (a magnitude and a direction, like velocity), a tensor field is a generalization of a ''scalar field'' and a ''vector field'' that assigns, respectively, a scalar or vector to each point of space. If a tensor is defined on a vector fields set over a module , we call a tensor field on . A tensor field, in common usage, is often referred to in the shorter form "tensor". For example, the ''Riemann curvature tensor'' refers a tensor ''field'', as it associates a tensor to each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinor Field
In differential geometry, given a spin structure on an n-dimensional orientable Riemannian manifold (M, g),\, one defines the spinor bundle to be the complex vector bundle \pi_\colon\to M\, associated to the corresponding principal bundle \pi_\colon\to M\, of spin frames over M and the spin representation of its structure group (n)\, on the space of spinors \Delta_n. A section of the spinor bundle \, is called a spinor field. Formal definition Let (,F_) be a spin structure on a Riemannian manifold (M, g),\,that is, an equivariant lift of the oriented orthonormal frame bundle \mathrm F_(M)\to M with respect to the double covering \rho\colon (n)\to (n) of the special orthogonal group by the spin group. The spinor bundle \, is defined to be the complex vector bundle =\times_\Delta_n\, associated to the spin structure via the spin representation \kappa\colon (n)\to (\Delta_n),\, where ()\, denotes the group of unitary operators acting on a Hilbert space .\, The spin represent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrostatic Field
An electric field (sometimes called E-field) is a physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) describes their capacity to exert attractive or repulsive forces on another charged object. Charged particles exert attractive forces on each other when the sign of their charges are opposite, one being positive while the other is negative, and repel each other when the signs of the charges are the same. Because these forces are exerted mutually, two charges must be present for the forces to take place. These forces are described by Coulomb's law, which says that the greater the magnitude of the charges, the greater the force, and the greater the distance between them, the weaker the force. Informally, the greater the charge of an object, the stronger its electric field. Similarly, an electric field is stronger nearer charged objects and weaker further away. El ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Law Of Universal Gravitation
Newton's law of universal gravitation describes gravity as a force by stating that every particle attracts every other particle in the universe with a force that is Proportionality (mathematics)#Direct proportionality, proportional to the product of their masses and Proportionality (mathematics)#Inverse proportionality, inversely proportional to the square of the distance between their centers of mass. Separated objects attract and are attracted Shell theorem, as if all their mass were concentrated at their centers. The publication of the law has become known as the "Unification (physics)#Unification of gravity and astronomy, first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors. This is a general physical law derived from empirical observations by what Isaac Newton called ''inductive reasoning''. It is a part of classical mechanics and was formulated in Newton's work ''Philosophiæ Natura ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |