|
Pentagrammic Crossed Antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams. This polyhedron is identified with the indexed name U80 as a uniform polyhedron. The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron. See also * Prismatic uniform polyhedron External links * *http://www.mathconsult.ch/showroom/unipoly/80.html * http://bulatov.org/polyhedra/uniform/u05.html * https://web.archive.org/web/20050313234519/http://www.math.technion.ac.il/~rl/kaleido/data/05.html Prismatoid polyhedra {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crossed Pentagrammic Antiprism
Crossed may refer to: * Crossed (comics), ''Crossed'' (comics), a 2008 comic book series by Garth Ennis * Crossed (novel), ''Crossed'' (novel), a 2010 young adult novel by Ally Condie * Crossed (The Walking Dead), "Crossed" (''The Walking Dead''), an episode of the television series ''The Walking Dead'' See also * *Crossed out (other) *Cross (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprisms
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556. The German form of the word "antiprism" was used for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can arise through truncation operations on regular simple or star polygons. Branko Grünbaum identified two primary usages of this terminology by Johannes Kepler, one corresponding to the regular star polygons with List of self-intersecting polygons, intersecting edges that do not generate new vertices, and the other one to the isotoxal Concave polygon, concave simple polygons.Grünbaum & Shephard (1987). Tilings and Patterns. Section 2.5 Polygram (geometry), Polygrams include polygons like the pentagram, but also compound figures like the hexagram. One definition of a ''star polygon'', used in turtle graphics, is a polygon having ''q'' ≥ 2 Turn (geometry), turns (''q'' is called the turning number or Density (polygon), density), like in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around the five points creates a similar symbol referred to as the pentacle, which is used widely by Wiccans and in paganism, or as a sign of life and connections. The word ''pentagram'' comes from the Greek language, Greek word πεντάγραμμον (''pentagrammon''), from πέντε (''pente''), "five" + γραμμή (''grammē''), "line". The word pentagram refers to just the star and the word pentacle refers to the star within a circle, although there is some overlap in usage. The word ''pentalpha'' is a 17th-century revival of a post-classical Greek name of the shape. History Early history Early pentagrams have been found on Sumerian pottery from Ur c. 3500 Common Era, BCE, and the five-pointed star was at various times the symbol of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Antiprism
In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It has 12 faces, 20 edges and 10 vertices. This polyhedron is identified with the indexed name U79 as a uniform polyhedron. Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter. In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon. Gallery Net Net (fold the dotted line in the centre in the opposite direction to all the other lines): : See also * Prismatic uniform polyhedron *Pentagrammic prism In geometry, the pentagrammic prism is one of an infinite set of nonconvex Pris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron
In geometry, a uniform polyhedron has regular polygons as Face (geometry), faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruence (geometry), congruent. Uniform polyhedra may be Regular polyhedron, regular (if also Isohedral figure, face- and Isotoxal figure, edge-transitive), Quasiregular polyhedron, quasi-regular (if also edge-transitive but not face-transitive), or Semiregular polyhedron, semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be Convex polyhedron, convex, so many of the uniform polyhedra are also Star polyhedron, star polyhedra. There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of Prism (geometry), prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 Quasiregular polyhedron, quasiregular and 11 Semiregular polyhedron, semiregular&m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Crossed-antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams. This polyhedron is identified with the indexed name U80 as a uniform polyhedron. The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron. See also * Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms. All have their vertices in parallel planes and are therefore prismato ... External links * *http://www.mathconsult.ch/show ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the ( convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , contai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Icosahedron
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra (nonconvex List of regular polytopes#Non-convex 2, regular polyhedra), with Schläfli symbol and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence. The great icosahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the -dimensional simplex faces of the core -polytope (equilateral triangles for the great icosahedron, and line segments for the pentagram) until the figure regains regular faces. The grand 600-cell can be seen as its four-dimensional analogue using the same process. Construction The edge length of a great icosahedron is \frac times that of the original icosahedron. Images Formulas For a great icosahedron with edge length E (the edge of its dodecahedron core), \text = \frac \text = \frac \text = \frac \text = 3\sqrt(5+4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equal distance and angles from a center point. Two polytopes share the same ''vertex arrangement'' if they share the same 0-skeleton. A group of polytopes that shares a vertex arrangement is called an ''army''. Vertex arrangement The same set of vertices can be connected by edges in different ways. For example, the ''pentagon'' and ''pentagram'' have the same ''vertex arrangement'', while the second connects alternate vertices. A ''vertex arrangement'' is often described by the convex hull polytope which contains it. For example, the regular ''pentagram'' can be said to have a (regular) ''pentagonal vertex arrangement''. Infinite tilings can also share common ''vertex arrangements''. For example, this triangular lattice of points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
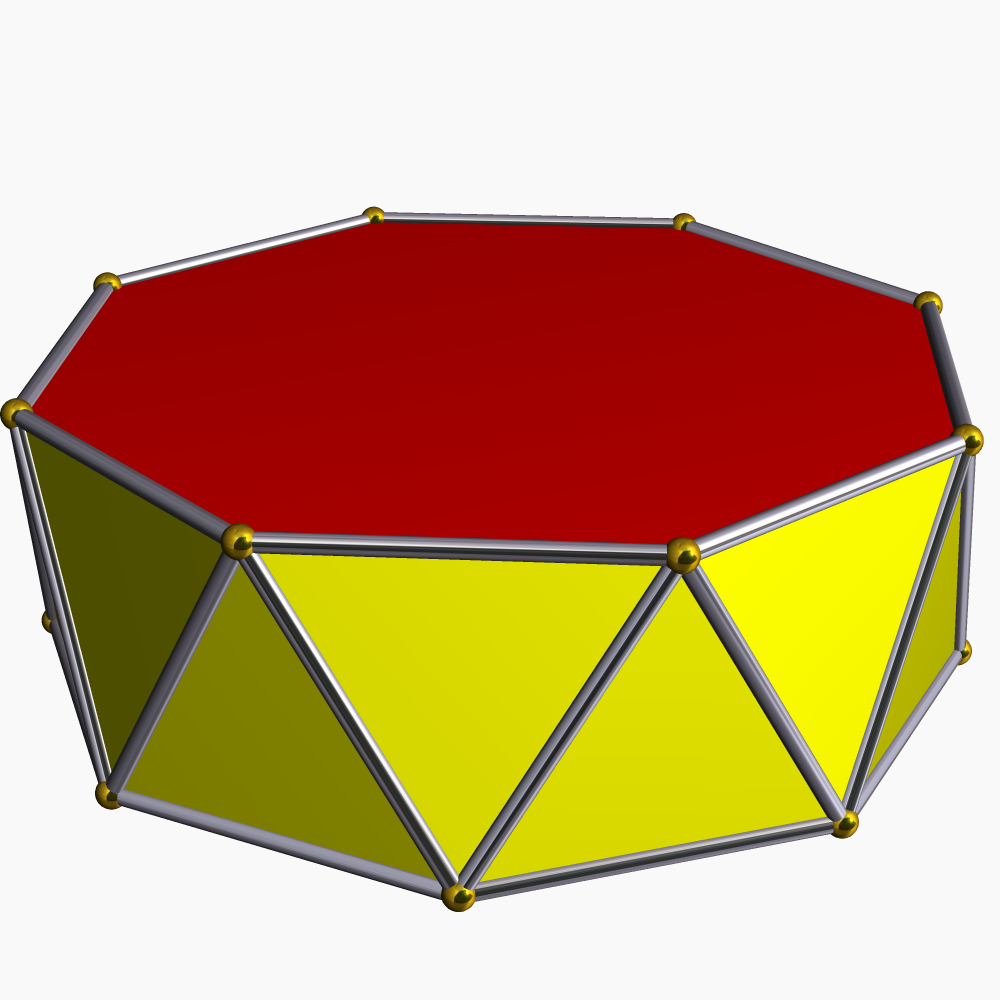
Pentagonal Antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of ten triangles for a total of twelve faces. Hence, it is a non-regular dodecahedron. Geometry If the faces of the pentagonal antiprism are all regular, it is a semiregular polyhedron. It can also be considered as a parabidiminished icosahedron, a shape formed by removing two pentagonal pyramids from a regular icosahedron leaving two nonadjacent pentagonal faces; a related shape, the metabidiminished icosahedron (one of the Johnson solids), is likewise form from the icosahedron by removing two pyramids, but its pentagonal faces are adjacent to each other. The two pentagonal faces of either shape can be augmented with pyramids to form the icosahedron. The semiregular pentagonal antiprism is inscribed in a cylinder whose bases are the disks in which the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |