|
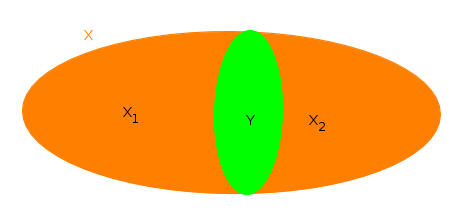
Path-connectedness
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is locally connected, which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topological space X the follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-connected Space
In algebraic topology, homotopical connectivity is a property describing a topological space based on the dimension of its holes. In general, low homotopical connectivity indicates that the space has at least one low-dimensional hole. The concept of ''n''-connectedness generalizes the concepts of path-connectedness and simple connectedness. An equivalent definition of homotopical connectivity is based on the homotopy groups of the space. A space is ''n''-connected (or ''n''-simple connected) if its first ''n'' homotopy groups are trivial. Homotopical connectivity is defined for maps, too. A map is ''n''-connected if it is an isomorphism "up to dimension ''n,'' in homotopy". Definition using holes All definitions below consider a topological space ''X''. A hole in ''X'' is, informally, a thing that prevents some suitably-placed sphere from continuously shrinking to a point., Section 4.3 Equivalently, it is a sphere that cannot be continuously extended to a ball. Formally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Connectedness
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is locally connected, which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topological space X the fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separated Sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way: roughly speaking, neither overlapping nor touching. The notion of when two sets are separated or not is important both to the notion of connected spaces (and their connected components) as well as to the separation axioms for topological spaces. Separated sets should not be confused with separated spaces (defined below), which are somewhat related but different. Separable spaces are again a completely different topological concept. Definitions There are various ways in which two subsets A and B of a topological space X can be considered to be separated. A most basic way in which two sets can be separated is if they are disjoint, that is, if their intersection is the empty set. This property has nothing to do with topology as such, but only set theory. Each of the following properties is stricter than disjoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clopen
In topology, a clopen set (a portmanteau of closed-open set) in a topological space is a set which is both open and closed. That this is possible may seem counterintuitive, as the common meanings of and are antonyms, but their mathematical definitions are not mutually exclusive. A set is closed if its complement is open, which leaves the possibility of an open set whose complement is also open, making both sets both open closed, and therefore clopen. As described by topologist James Munkres, unlike a door, "a set can be open, or closed, or both, or neither!" emphasizing that the meaning of "open"/"closed" for is unrelated to their meaning for (and so the open/closed door dichotomy does not transfer to open/closed sets). This contrast to doors gave the class of topological spaces known as " door spaces" their name. Examples In any topological space X, the empty set and the whole space X are both clopen. Now consider the space X which consists of the union of the two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singleton (mathematics)
In mathematics, a singleton (also known as a unit set or one-point set) is a set with exactly one element. For example, the set \ is a singleton whose single element is 0. Properties Within the framework of Zermelo–Fraenkel set theory, the axiom of regularity guarantees that no set is an element of itself. This implies that a singleton is necessarily distinct from the element it contains, thus 1 and \ are not the same thing, and the empty set is distinct from the set containing only the empty set. A set such as \ is a singleton as it contains a single element (which itself is a set, but not a singleton). A set is a singleton if and only if its cardinality is . In von Neumann's set-theoretic construction of the natural numbers, the number 1 is ''defined'' as the singleton \. In axiomatic set theory, the existence of singletons is a consequence of the axiom of pairing: for any set ''A'', the axiom applied to ''A'' and ''A'' asserts the existence of \, which is the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example, The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface , or blackboard bold A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Subset
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a closed set is a set which is closed under the limit operation. This should not be confused with closed manifold. Sets that are both open and closed and are called clopen sets. Definition Given a topological space (X, \tau), the following statements are equivalent: # a set A \subseteq X is in X. # A^c = X \setminus A is an open subset of (X, \tau); that is, A^ \in \tau. # A is equal to its closure in X. # A contains all of its limit points. # A contains all of its boundary points. An alternative characterization of closed sets is available via sequences and nets. A subset A of a topological space X is closed in X if and only if every limit of every net of elements of A also belongs to A. In a first-countable space (such as a me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjoint Sets
In set theory in mathematics and Logic#Formal logic, formal logic, two Set (mathematics), sets are said to be disjoint sets if they have no element (mathematics), element in common. Equivalently, two disjoint sets are sets whose intersection (set theory), intersection is the empty set.. For example, and are ''disjoint sets,'' while and are not disjoint. A collection of two or more sets is called disjoint if any two distinct sets of the collection are disjoint. Generalizations This definition of disjoint sets can be extended to family of sets, families of sets and to indexed family, indexed families of sets. By definition, a collection of sets is called a ''family of sets'' (such as the power set, for example). In some sources this is a set of sets, while other sources allow it to be a multiset of sets, with some sets repeated. An \left(A_i\right)_, is by definition a set-valued Function (mathematics), function (that is, it is a function that assigns a set A_i to every ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Of A Set
In mathematics, a partition of a set is a grouping of its elements into Empty set, non-empty subsets, in such a way that every element is included in exactly one subset. Every equivalence relation on a Set (mathematics), set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory. Definition and notation A partition of a set ''X'' is a set of non-empty subsets of ''X'' such that every element ''x'' in ''X'' is in exactly one of these subsets (i.e., the subsets are nonempty mutually disjoint sets). Equivalently, a family of sets ''P'' is a partition of ''X'' if and only if all of the following conditions hold: *The family ''P'' does not contain the empty set (that is \emptyset \notin P). *The union (set theory), union of the sets in ''P'' is equal to ''X'' (that is \textstyle\bigcup_ A = X). The sets in ''P'' are said ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, a Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. When quantified, A \subseteq B is represented as \forall x \left(x \in A \Rightarrow x \in B\right). One can prove the statement A \subseteq B by applying a proof technique known as the element argument:Let sets ''A'' and ''B'' be given. To prove that A \subseteq B, # suppose that ''a'' is a particular but arbitrarily chosen element of A # show that ''a'' is an element of ''B''. The validity of this technique ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximal Element
In mathematics, especially in order theory, a maximal element of a subset S of some preordered set is an element of S that is not smaller than any other element in S. A minimal element of a subset S of some preordered set is defined dually as an element of S that is not greater than any other element in S. The notions of maximal and minimal elements are weaker than those of greatest element and least element which are also known, respectively, as maximum and minimum. The maximum of a subset S of a preordered set is an element of S which is greater than or equal to any other element of S, and the minimum of S is again defined dually. In the particular case of a partially ordered set, while there can be at most one maximum and at most one minimum there may be multiple maximal or minimal elements. Specializing further to totally ordered sets, the notions of maximal element and maximum coincide, and the notions of minimal element and minimum coincide. As an example, in the collecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |